以前常看的不外乎就是求一元二次方程式的根及解聯立方程式
1. 求根
我們常寫成 ax**2 + bx + c = 0

公式為
r1 = (-b + (b**2 - 4*a*c)**0.5) / 2*a
r2 = (-b - (b**2 - 4*a*c)**0.5) / 2*a
我們會利用 b**2 - 4ac來判斷，有三種情況：
1. b**2 - 4ac為正，解為兩實數根
2. b**2 - 4ac為0，解為一實數根
3. b**2 - 4ac為負，沒有實數根

接下來我們來舉例

一元二次方程式為 2x**2 + 5x + 6 = 0

a = 2
b = 5
c = 6

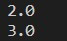
r1 = (-b + (b**2 - 4*a*c)**0.5) / 2*a
r2 = (-b - (b**2 - 4*a*c)**0.5) / 2*a
print(r1)
print(r2)

2. 解聯立
最簡單，有兩條方程式
ax + by = e
cx + dy = f

假設 2x + 3y = 13
     x - 2y = -4

a = 2
b = 3
c = 1
d = -2
e = 13
f = -4

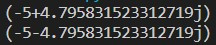
x = (e*d - b*f) / (a*d - b*c)
y = (a*f - e*c) / (a*d - b*c) #若a*d - b*c = 0，此方程式無解
print(x)
print(y)