今天要介紹的是 loss function，中文翻成損失函數或誤差函數。它是一個在機器學習中讓我們「評估 model 好壞的指標」，判斷目前模型與我們期望的目標(object function)差多少。

我們在使用損失函數指標的時候會希望誤差越小越好，而這邊將介紹幾個在使用這個指標時常聽到的方法，如 均方誤差(MSE, Mean Square Error)、平均絕對值誤差(MAE, Mean Absolute Error) 和 交叉熵(cross-entropy)，它們適合用在什麼樣的問題將會一一說明。

一、迴歸問題常用的損失函數－均方誤差(MSE, Mean Square Error)、平均絕對值誤差(MAE, Mean Absolute Error)

圖片來源：嗡嗡的 Google machine learning 學習筆記系列第20篇 -【Day 20】 Google ML - Lesson 6 - 使用損失函數(Loss Functions)來評估ML模型的好壞吧! MSE, RMSE, Cross Entropy的計算方法與特性

先講一下均方誤差(MSE, Mean Square Error)的意思。通常我們講或計算誤差，最直覺的方法就是相減，把所有預測值與目標的差距相加後得到結果。但由於這些差距值有正有負，直接相加會有抵銷距離的情形，所以這時候我們就把它平方再相加，避開這個問題。

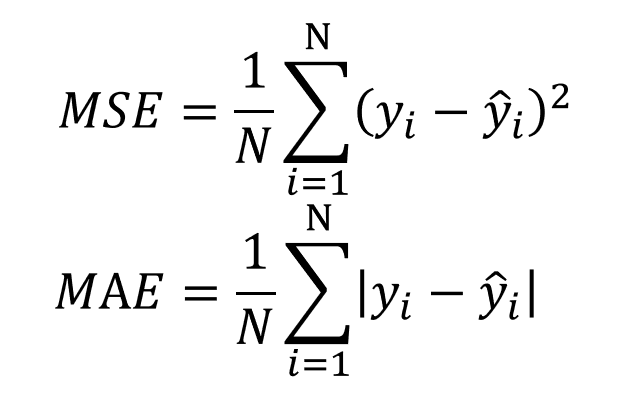
當然也可以用絕對值讓差值變正數，也就是平均絕對值誤差(MAE, Mean Absolute Error)，但我們會比較常使用平方的方法是因為可以整體微分。MSE跟MAE這兩種方法在迴歸上都可以幫我們判斷目前模型與我們期望的目標(object function)差多少，所以它們是迴歸問題上常用的損失函數。

ps. 這兩種方法也會拿去做正規化(Regularization)，有機會後面會提到。

二、分類問題常用的損失函數－交叉熵(cross-entropy)

什麼是熵(entropy)？物理學翻成亂度，這邊我借用一下決策樹的節點選擇概念(Information Gain)，來較為視覺化的解釋這個詞的意義。決策樹是透過去選擇根據某些屬性分類後，資料分出來的效果好、資料同質性較高(pure)的屬性作為節點，如圖有兩個屬性，而我們會選擇 attribute1 作為節點。

圖片來源：陳冠億 Kenny 的 資料分析系列-探討決策樹(1)

那怎麼用數值化的方式去比較節點的好壞呢？其計算方式就是利用熵(entropy)。結合上下圖舉例來說，我們現在有 12 顆紅球跟 12 個綠三角形，現在我們想要將紅球綠三角型分成兩袋，然後算在袋子裡取出與袋中其他物品不一樣類型的機率(不確定性)。根據屬性 1 和屬性 2 我們得到兩種分類，在屬性 1 左邊取到不一樣類型的物品的機率(p)為 1/12，取到一樣的機率(q)為11/12，屬性 1 左右兩邊計算後再加權，對比屬性 2 依同樣方式計算後，屬性 1 的熵算起來比較小，比較不容易拿錯。如果將其測量不確定性概念用在其他地方，也就是當熵越小，亂度越不亂，資料同質性高，效果越好。

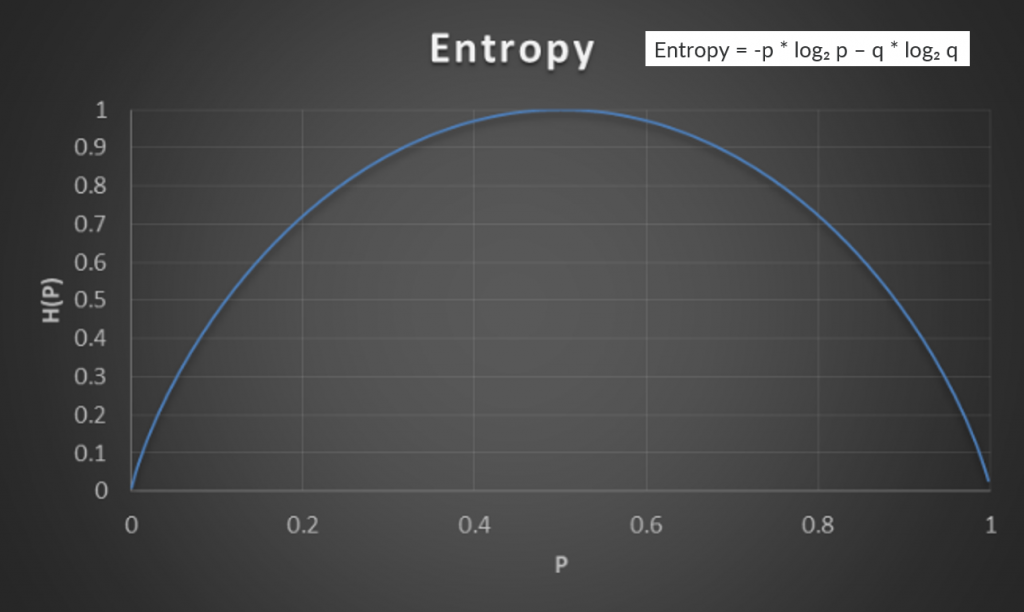
圖片來源：Tommy Huang 的 機器/深度學習: 基礎介紹-損失函數(loss function)

扯得有點遠了回到正題，那什麼是交叉熵(cross entropy)？entropy entropy cross 嗎(好冷)，但其實cross entropy 就是去計算每個類別的entropy，然後再去做加總。所以我們在讓模型分類時，我們會希望 cross entropy 越小越好，因為這代表這個模型與我們期望的目標(object function)差的越來越小。

這邊可能會有一個疑問，為什麼做分類問題時，是用 cross entropy 作為損失函數而不是 MSE 呢？

我的看法是，MSE 算的是距離，cross entropy算的是機率。分類問題的類別彼此是獨立的，在距離空間中並沒有任何意義。

三、小結

這幾天我們會介紹在用 Keras 疊一個手寫數字辨識神經網路時，需要先知道的幾個名詞。今天講的是損失函數或說誤差函數(loss)這個幫我們評估 model 好壞的指標，並重點提了兩個常見的方法。它的細節與分類還有很多，如果有興趣可以看一下 Keras 提供的套件。

[註1]這邊非常推薦看 機器/深度學習: 基礎介紹-損失函數(loss function) 一文瞭解更多更清楚例子