今天會帶大家來看看隸屬函數，這個說簡單不簡單說難也不難的函數到底長甚麼樣呢？一起來一探究竟吧。這邊會介紹幾個常用的隸屬函數，其規則跟一些特性需要注意一下。通常會把每個觀察值都模糊化成3個以上的值，而每個值都介於0~1。

隸屬函數—Triangular mf(三角)

這個函數最基礎長這樣，當輸入一個值後出來的結過會是三個值，中間紅色的三角部分是被允許可以有不只一個的，如果中間三角的部分有兩個，那加上前後藍線跟綠線的畫出來的結果就會變成一組四個元素的陣列。以下圖舉例來說，如果輸入是1的話那他就在最左邊的藍線上，結果就是[1,0,0]，輸入是2跟的輸出也是[1,0,0]，輸入是3.75的話輸出就是[0.5,0.5,0]。

不知道各位有沒有發現這種隸屬函數的輸出不管被拆成了幾個元素，其總和都要等於1，基本上斜率多少跟線的位置等都沒有硬性規定，完全隨各位喜好，遵循總和等於1就好了。

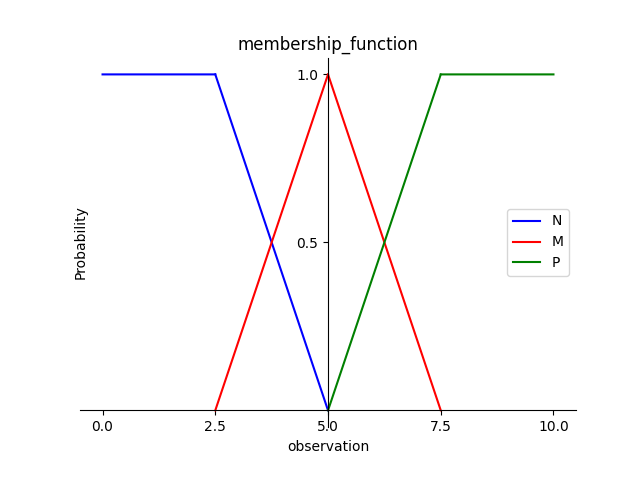
程式碼如下，基本上只需要幾段判斷式就好了，obs代表輸入的觀察值，min_obs跟max_obs代表此觀察值的最大值跟最小值。d1,d2,d3就像上圖的2.5、5.0、7.5，為將隸屬函數分段的部分。接下來就是判斷值落在哪個區間，並且算出值來而已。

def triangular_mf(obs, min_obs, max_obs):
    d1 = min_obs + (max_obs - min_obs) * 1/4
    d2 = (max_obs + min_obs) * 1 / 2
    d3 = min_obs + (max_obs - min_obs) * 3/4
    n = m = p = 0
    if obs <= d1:
        n = 1
        m = 0
        p = 0
    elif (obs > d1 and obs <= d2):
        n = (obs - d2) / (d1 - d2)
        m = (obs - d1) / (d2 - d1)
        p = 0
    elif (obs > d2 and obs <= d3):
        n = 0
        m = (obs - d3) / (d2 - d3)
        p = (obs - d2) / (d3 - d2)
    elif (obs > d3):
        n = 0
        m = 0
        p = 1
    return [n,m,p]

隸屬函數—Gaussian&Sigmoid mf

這大概是我最愛用的函數了，我第一個專案就是使用這個隸屬函數，之後就把模板存起來，往後的專案若需要模糊控制就會直接套用。

這組隸屬函數的組成是兩條sigmoid函數(綠色跟橘色)，以及一條高斯函數(常態分布)的曲線。

先從sigmoid開始說起，他同時也是類神經網路的輸出函數中的其中一種，他的值域落在0~1，數學方程式為：

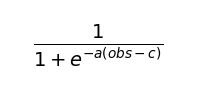
a是中間傾斜的程度；c為控制函數水平平移的程度。

高斯函數(常態分佈)的特點就是就是函數左右的值都很低，所以跟sigmoid搭配剛剛好，常態分佈的數學方程式為：

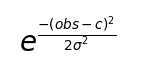
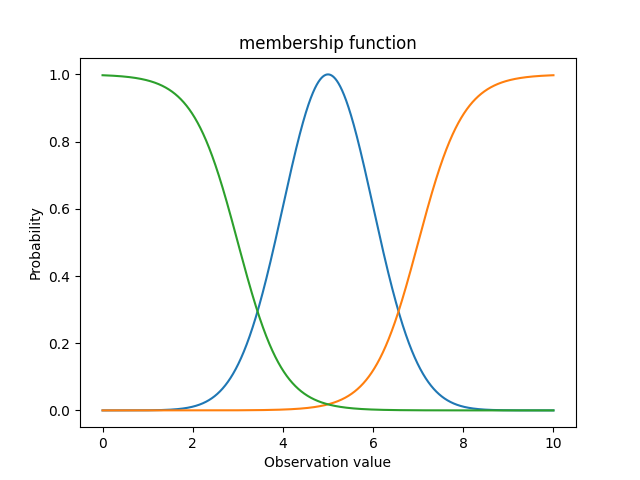
σ為函數的寬度；c為控制函數水平平移的程度。

也有很多純高斯函數組合的，此種函數就沒有規定函數組出來總和要是1了，所以各位就可以自由搭配。別弄得太複雜都好~

其他隸屬函數

上述兩個函數分別是最基礎的，以及我最常用的~不過還是會將其他簡單的隸屬函數簡單介紹一遍~

1.Trapezoidal mf(梯形)

此隸屬函數顧名思義就是很多梯型組合而成的，函數設定的方式跟Triangular mf差不多。這也是我沒怎麼在使用的函數，不過使用起來也沒太大問題。

圖源

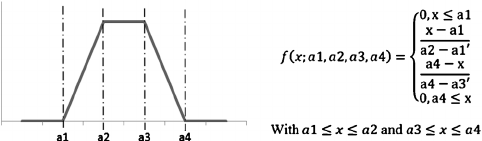
2.GeneralizedBell mf(鍾型)

此隸屬函數有點像高斯函數跟梯形函數的合體，函數左右的值都快速地變小，但函數上方卻是比較平坦的。函數方程式為：

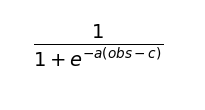
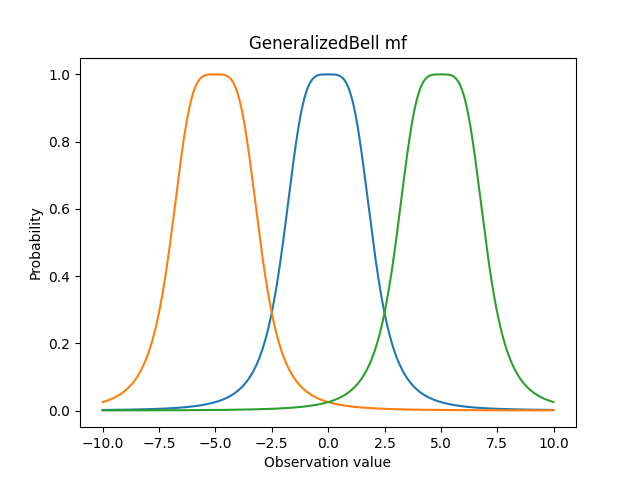
a為控制函數的寬度；b為控制上面函數的平坦程度；c為控制函數水平平移的程度。

結語

隸屬函數介紹就到這邊，明天開始會帶大家實際將觀察值模糊化，因為時間關係無法所有函數都詳細介紹，對於這部分可能有一些不詳盡的地方，如過果想更深入了解的話，各位也可以到下列網址看看。就我所知，隸屬函數非常多種，只要用的好你也可以自創屬於你自己的隸屬函數喔。

明天會帶大家進行觀察值的採樣跟加入模糊控制，接下來各位就可以測試看看模糊控制與否對訓練的成功率的比較了，模糊控制說實在的不一定有用，不過實驗就是要多方嘗試。有可能會遇到驚喜，也有可能意外突破瓶頸~

參考資料、網址

What is fuzzy membership function - A complete guide