學習設計的人在使用Adobe Illustrator這類向量繪圖軟體的時候，都會使用一種鋼筆工具。

這個工具會產生控制桿，設計人員可以利用這個控制桿來擬合已有的圖形曲線，或是創造自己希望的曲線，而這種曲線便是貝茲曲線。

貝茲曲線由保爾·德·卡斯特里奧（Paul de Casteljau）於1959年開發，法國工程師皮埃爾·貝茲（Pierre Bézier）運用貝茲曲線來為汽車的主體進行設計，並廣泛發表。

今天就來介紹貝茲曲線的原理，還有如何在JSXGraph中使用它。

貝茲曲線原理

假設給定平面上兩個點 和 ，則對應這兩點的貝茲曲線就是通過這兩點的線段，也就是一次貝茲曲線，可以表示為 ， ，給定三個點 ，假設 是對應 和 的一次貝茲曲線， 是對應 和 的一次貝茲曲線，則對應這三點的貝茲曲線為 ，　此時 為控制點，同理可推廣至三次貝茲曲線（Cubic Bezier Curve），此時會有二個控制點，一般繪圖軟體使用的貝茲曲線，便是三次貝茲曲線。

利用貝茲曲線的原理，我們可以在JSXGraph作出三次貝茲曲線，執行成果如下圖。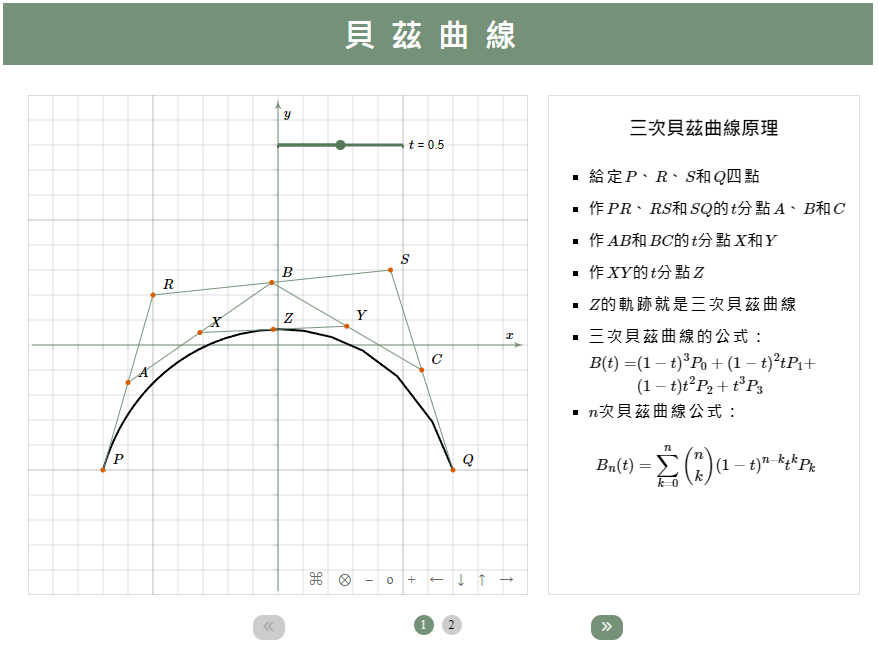

其中A、D是資料點，而B、C是控制點。

JSXGraph內為貝茲曲線

JSXGraph本身就有內建貝茲曲線可以使用，其方法為JXG.Math.Numerics.bezier(p)，其中p為一陣列，存放資料點和控制點，共有3k+1個元素，k=1, 2, 3, ...；其中第p[3k]元素為資料點，p[3k+1]和p[3k+2]為控制點。

let p = [];

let color = 'red'; 
p.push(board2.create('point',[7,1],{strokeColor:color,fillColor:color, name: '\\(A\\)'}))       // data point
color = 'blue'
p.push(board2.create('point',[3,7],{strokeColor:color,fillColor:color, name: '\\(B\\)'}))  // control point
p.push(board2.create('point',[-2,6],{strokeColor:color,fillColor:color, name: '\\(C\\)'}))  // control point

color = 'red'
p.push(board2.create('point',[-6,1],{strokeColor:color,fillColor:color, name: '\\(D\\)'}))      // data point

let bezier = board2.create('curve', JXG.Math.Numerics.bezier(p), 
               {strokecoloror:'blue', strokeOpacity:0.6, strokeWidth:5})

執行結果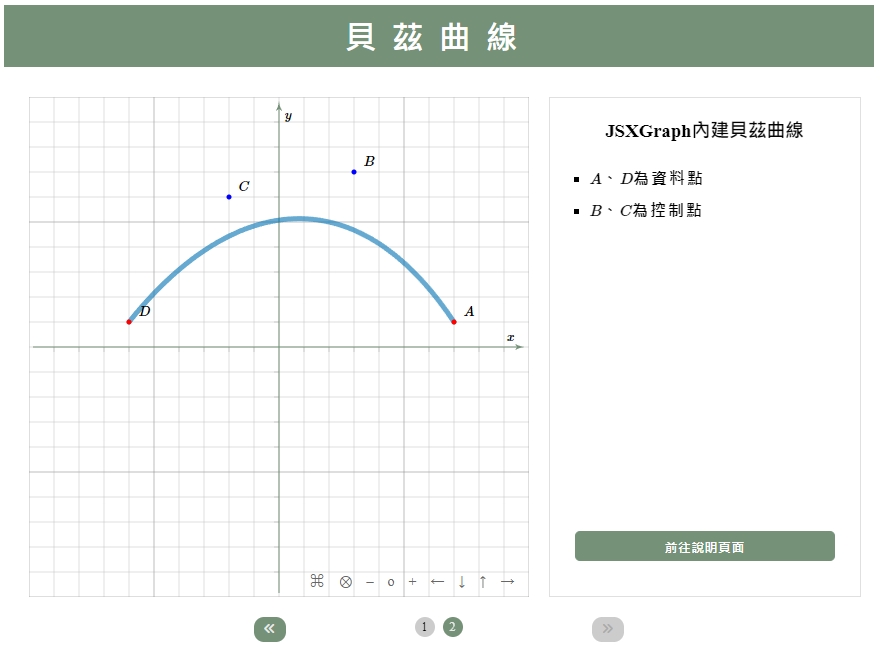

程式原始碼

今日程式原始碼

今日小結

函數擬合一直是數值分析在工程和設計上非常重要的應用，今天談到的貝茲曲線已經是設計人員必須精熟的技巧；另外貝茲曲線的延伸B-Spline曲線則是使用分段擬合的精神來進行擬合，在工程上和設計上的應用也很多，JSXGraph也有提供JXG.Math.Numerics.bezier(p, order)方法，連續兩天介紹數學的應用，希望能激發更多人學習數學的熱情，明天見！