眾所皆知，「龜兔賽跑」的勝利者是龜，今天就用小海龜來模擬CNC繪圖機畫直線。

布雷森漢姆直線演算法

一般人大概很難想像給定兩點畫直線有何困難，只要拿隻尺，將尺靠在兩點上，就可以輕而易舉的畫好直線。在連續的世界裏，畫直線的確不難，然而在電腦的世界，螢幕上的格點是離散的，每一個格點只能決定亮或不亮，因此需要一個演算準則來決定，而布雷森漢姆直線演算法（Bresenham's line algorithm）便是為了解決這個問題而發展的演算法，是電腦圖學中非常基本而重要的演算法。這個演算法其實並不難懂，也非常精簡，常被實作在繪圖晶片和繪圖程式庫中。

CNC繪圖機中有兩個步進馬達來驅動繪圖機的噴頭，一個負責水平方向，另一個負責垂直方向，每個脈衝訊號進來，前進一步或不動，因此CNC繪圖機也有類似的問題，所以也可以使用布雷森漢姆直線演算法。我們先將顯示今天執行的結果，用圖來說明布雷森漢姆直線演算法。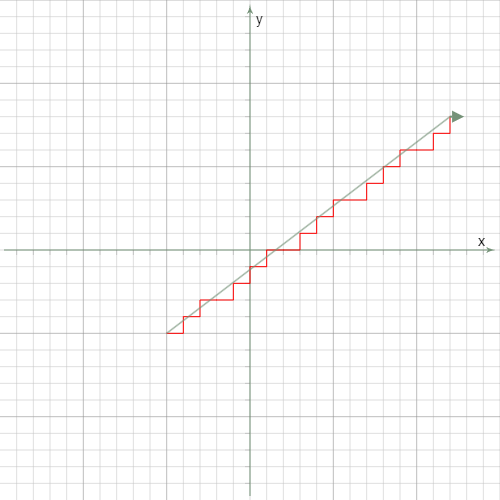

假設我們畫一條連接(-5, -5)和(12, 8)的直線，布雷森漢姆直線演算法的邏輯很簡單，水平方向要走12-(-5)=17格，鉛直方向要走8-(-5)=13格，我們先計算這條直線的斜率為13/17，代表每水平向右走一格，直線要向上走13/17格，但是前面說到我們必須決定要向上走一格或是停留不動。用四捨五入的決定準則，如果超過0.5，那便向上一格，並減去1（因為已經往上走了1格）；反之，則停留不動。因為13/17為浮點數，運算速度比較慢，而且會累積運算誤差，因此將所有計算同乘分母17，所以每向右走一步，鉛直方向便加13，如果超過[17/2]=8，我們就向上，而且減去17；反之便停留不動。

以實例來看鉛直方向起始值為0，

• 第一步向右，0+13>8，所以鉛直方向往上一格，13-17=-4；
• 再向右一格，-4+13=9>8，鉛直方向往上一格，9-17=-8；
• 再向右一格，-8+13=5<8，鉛直方向停留不動。
• 再向右一格，5+13=18>8，鉛直方向往上一格，18-17=1；
• 依序下去…。

上圖是是這個演算邏輯的結果，紅色折線會跟著直線前進。

Turtle元素

先建立Turtle元素

const turtle = board1.create('turtle')
turtle.setPosition(-5, -5)
turtle.fd(1)
trutle.rt(90)
trutle.lt(90)

fd是foward的縮寫，參數1代表走1格，rt是right的縮寫，參數90代表向右轉90度；lt則代表left。
布雷森漢姆直線演算法Javascript實作

async function drawLine(x1, y1, x2, y2) {
  turtle.setPos(x1, y1)
  const dy = y2 - y1
  const dx = x2 - x1
  const absDy = Math.abs(dy)
  const absDx = Math.abs(dx)
  const threshold = parseInt(absDx / 2)
  let over = 0
  if (absDx >= absDy) {
    if (dx > 0) {
      turtle.rt(90)
    } else {
      turtle.lt(90)
    }
    for (let i = 1; i <= absDx; i++) {
      turtle.fd(1)
      over += absDy
      if (over > threshold) {
        if (dy * dx > 0) {
          turtle.lt(90)
          turtle.fd(1)
          turtle.rt(90)
        } else {
          turtle.rt(90)
          turtle.fd(1)
          turtle.lt(90)
        }
        over -= absDx
      }
      await sleep(1000)
    }
  }
}

為了能仔細看小海龜行進的過程，我們用Promise模擬了sleep()函式。

function sleep(millisecond) {
  return new Promise(resolve => {
    setTimeout(() => {
      resolve()
    }, millisecond)
  })
}

這邊只列出斜率小於1的情況，斜率大於1的時候，x和y的角色調換，y每次向上走一格，再決定x是向右一格還是停留原地。

程式原始碼

今日程式原始碼

今日小結

小海龜將來可以擴展模擬執行CNC機器Gcode的控制器，這將是一個有趣的計畫，希望有時間可以執行。布雷森漢姆直線演算法可擴展至畫圓及橢圓，裏面會用到微積分和更多的因式分解，對數學應用有興趣的人可以深入研究。明天會再利用小海龜來畫Koch等碎形相關的曲線，並介紹L-System，明天見！