Merge Sorted Array

題目說明

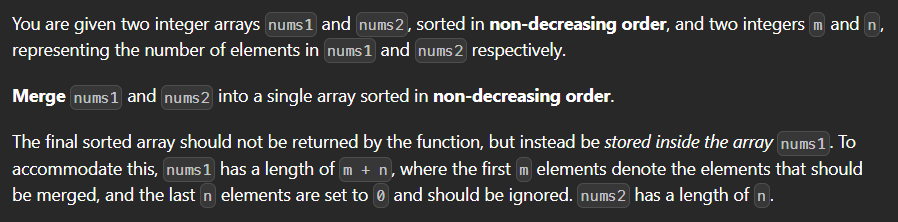
給定兩組非遞減的整數陣列 nums1 和 nums2，其元素個數分別為 m 和 n，長度為 m+n 和 n。
需合併兩陣列至 nums1 並維持遞增排序。
不需要回傳值，將合併後答案填入 nums1(長度為 m+n，預留空間補0)，即不希望應用到額外的空間。

範例

Example 1:
Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]
Explanation: The arrays we are merging are [1,2,3] and [2,5,6].
The result of the merge is [1,2,2,3,5,6] with the underlined elements coming from nums1.

Example 2:
Input: nums1 = [1], m = 1, nums2 = [], n = 0
Output: [1]
Explanation: The arrays we are merging are [1] and [].
The result of the merge is [1].

Example 3:
Input: nums1 = [0], m = 0, nums2 = [1], n = 1
Output: [1]
Explanation: The arrays we are merging are [] and [1].
The result of the merge is [1].
Note that because m = 0, there are no elements in nums1. The 0 is only there to ensure the merge result can fit in nums1.

限制條件和特別需求

• nums1.length == m + n
• nums2.length == n
• 0 <= m, n <= 200
• 1 <= m + n <= 200
• -109 <= nums1[i], nums2[j] <= 109
  Follow up: Can you come up with an algorithm that runs in O(m + n) time?

思路

一開始直覺想把 nums2 的值塞到 nums1 裡，既然都已經升序排列那就只要比對 nums1 的前後值並塞進去就可以吧，但這樣遇到後面補0的時候會需要再多很多判斷避免問題，也造成多出額外空間事後要刪掉，這想法行不通!!!那還有沒有其他作法呢?

後來發現其實題目已經給了很多線索，已預留的空間和排序好的遞增數列。利用上述特性可以分別從後面兩兩比對值，將較大的值填到 nums1 的最後面，較小的值則繼續與另一個值比對，直到 nums1 被填完即比對完畢，並且沒有任何值有被覆蓋掉的問題。

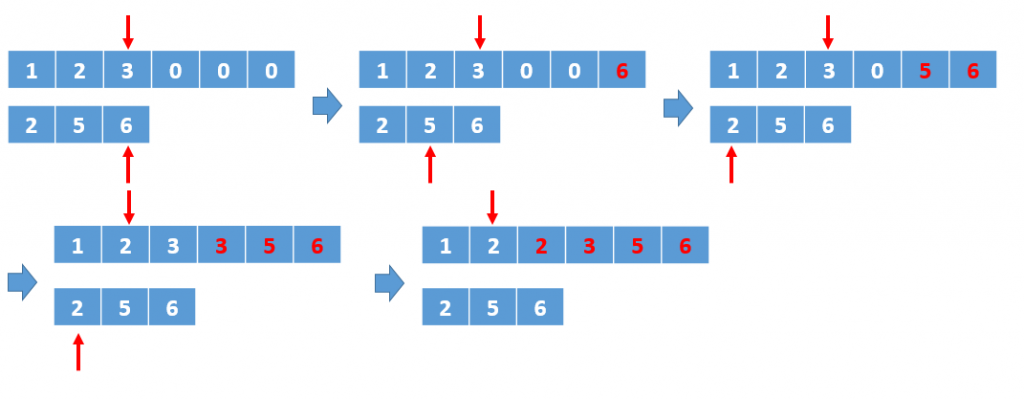
根據此方向，有三個狀況要解決

• m=0,即把所有的 nums2 依序填到 nums1
• n=0，即 nums1 目前就是答案，不需額外做事
• m, n !=0，即需要由後往前各自比對，並將較大的數放入 nums1 的最後面

C++ 程式碼

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
              
        for (int i=m+n-1; i>-1; i--) {
            if (m==0) {
                nums1[i] = nums2[n-1];
                n--;
                continue;
            }
        
            if (n==0)
                break;
            
            if (nums1[m-1] <= nums2[n-1]) {
                nums1[i] = nums2[n-1];
                n--;
            }
            else {
                nums1[i] = nums1[m-1];
                m--;
            }
        }
    }
};

Python3 程式碼

class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
    
        for i in range(m+n-1, -1, -1):
            if(m==0):
                nums1[i] = nums2[n-1]
                n = n-1
                continue
            if(n==0):
                break
                
            if(nums1[m-1] <= nums2[n-1]):
                nums1[i] = nums2[n-1]
                n = n-1
            else:
                nums1[i] = nums1[m-1]
                m = m-1