簡單的模組觀念就先暫時說到這邊,我們先用之前所學的觀念來實作 BCD 加法器!
數字的編碼方式其實有很多種,舉例來說,十進位是生活中常用的數字表示方式、二進位是電腦科學中最基本的表示方式。現在要介紹的 BCD 可以說是二進位和十進位的結合。BCD 全名為 Binary-Coded Decimal 意思是我們的單位還是十進位 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9),但是每一個數字都是由二進位的 0, 1 來表示,因此 BCD 的外在樣貌還是二進位。
我們先列出各個數字分別代表的 BCD 編碼:
| Decimal | BCD | Decimal | BCD | |
|---|---|---|---|---|
| 0 | 0000 | 5 | 0101 | |
| 1 | 0001 | 6 | 0110 | |
| 2 | 0010 | 7 | 0111 | |
| 3 | 0011 | 8 | 1000 | |
| 4 | 0100 | 9 | 1001 |
再多舉一些例子,二位的數字要怎麼表示呢?
| Decimal | BCD | Decimal | BCD | |
|---|---|---|---|---|
| 10 | 00010000 | 15 | 00010101 | |
| 11 | 00010001 | 16 | 00010110 | |
| 12 | 00010010 | 17 | 00010111 | |
| 13 | 00010011 | 18 | 00011000 | |
| 14 | 00010100 | 19 | 00011001 |
透過這些例子,不知道你有沒有發現 BCD 編碼的特色?
每一位十進位數字都是由 4 個二進位表示,因此透過 BCD 編碼,我們可以清楚知道原本的十進位有幾個數字。
先從電路圖看起 (圖片來源:Javatpoint)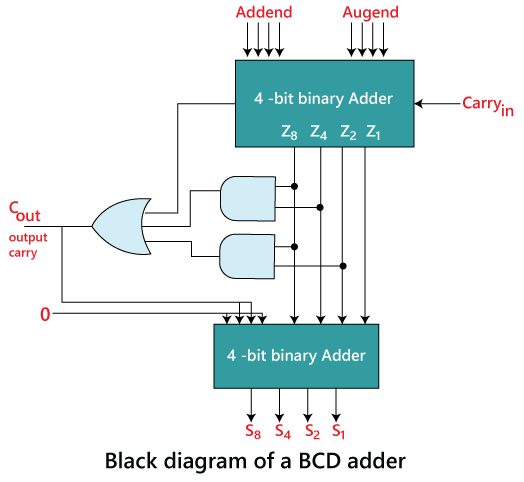
前面提到 BCD 其實是用二進位表示十進位,所以 BCD 的加法器理論上也要是用二進位加法器來去實作。不只如此,因為 BCD 是用 4 個二進位表示,所以他需要搭配 4 位元的加法器。
那麼 BCD 加法器跟 4 位元加法器的差異在哪裡呢?
當加法的和小於 10 時,這兩者其實沒有差異。但是當進位出現時,一個 4 位元加法器無法完整處理 BCD 的進位。因為二進位的 10 是 1010 ,但是 BCD 的 10 是 00010000 ,兩者有很大的差異。那要如何處理這件事呢?
從上面的電路圖可以看到 4 位元加法器的輸出會先經過一系列的邏輯閘產生進位訊號,再透過第二個 4 位元加法器產生最後的結果。這個說明其實有點抽象,我們分成幾個部分來說明:
如果產生進位,那應該會有 8 個輸出訊號,為什麼電路圖上只有 5 個輸出訊號?
我們先思考一個問題,兩個 BCD 碼搭配一個 Carry In ,最大是多少?是 19 喔!
所以十位數不是 1 就是 0 ,一個訊號其實就足以表示了。如果使用 4 個訊號來表示,其實是有些浪費了,因為前三個訊號一定是 0 。
「一系列的邏輯閘」,為什麼是這些邏輯閘?
要知道使用哪些邏輯閘,我們必須先找到相對應的布林表示式 (我們沿用上圖的代號,以 Z8 來表示 MSB,C' 為第一個 4 位元加法器的 Carry Out) ,即 Cout(C', Z8, Z4, Z2, Z1)。只要是找布林表示式,第一步驟一定是先畫出真值表:
| Decimal | C' | Z8 | Z4 | Z2 | Z1 | Cout |
|---|---|---|---|---|---|---|
| 00 | 0 | 0 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 | 1 | 0 |
| 02 | 0 | 0 | 0 | 1 | 0 | 0 |
| 03 | 0 | 0 | 0 | 1 | 1 | 0 |
| 04 | 0 | 0 | 1 | 0 | 0 | 0 |
| 05 | 0 | 0 | 1 | 0 | 1 | 0 |
| 06 | 0 | 0 | 1 | 1 | 0 | 0 |
| 07 | 0 | 0 | 1 | 1 | 1 | 0 |
| 08 | 0 | 1 | 0 | 0 | 0 | 0 |
| 09 | 0 | 1 | 0 | 0 | 1 | 0 |
| 10 | 0 | 1 | 0 | 1 | 0 | 1 |
| 11 | 0 | 1 | 0 | 1 | 1 | 1 |
| 12 | 0 | 1 | 1 | 0 | 0 | 1 |
| 13 | 0 | 1 | 1 | 0 | 1 | 1 |
| 14 | 0 | 1 | 1 | 1 | 0 | 1 |
| 15 | 0 | 1 | 1 | 1 | 1 | 1 |
| 16 | 1 | 0 | 0 | 0 | 0 | 1 |
| 17 | 1 | 0 | 0 | 0 | 1 | 1 |
| 18 | 1 | 0 | 0 | 1 | 0 | 1 |
| 19 | 1 | 0 | 0 | 1 | 1 | 1 |
有了真值表,我們可以透過 5 變數的卡諾圖化簡,結果應為 *Cout(C', Z8, Z4, Z2, Z1) = C' + Z3 x Z2 + Z3 x Z1* ,因此我們共需要兩個 And-Gate 和一個 3 個輸入的 Or-Gate。
第二個 4 位元加法器的被加數是第一個 4 位元加法器的結果,那麼加數是什麼?
加數的意義可以思考成這個數可以讓原本的結果強制進位,最大的 BCD 碼為 9 (十進位的 9),進位後變成 BCD 的 10 (十進位的 16),這中間的差距其實是 6 !而加數的第二個和第三個位元之所以是浮動的原因是我們也許根本不需要改變輸出,第一個加法器的結果也許就已經是最終的結果了!因此這兩個位元的數值會交由進位訊號來決定,MSB 和 LSB 則固定為 0 ,可以直接指定。
先觀察一下 BCD 加法器的電路圖,我們可以發現我們所需要的零件有:4 位元加法器、基本邏輯閘(And-Gate, Or-Gate) 。其中, 4 位元加法器還可以被我們拆解成 4 個全加器。
因此,想要完成 BCD 加法器,我們必須要做出三種模組,分別為 BCD_Adder, Adder4, Full_Adder 。
先從最小的元件 Full_Adder 開始。
根據全加器的真值表,我們可以推得輸入 (A, B, Cin) 與輸出 (Sum, Cout) 的布林關係式
Full Adder 的程式碼撰寫共有兩種方式,一種是使用 Gate Level Modeling ,另一種是使用 Dataflow Modeling 。
我使用 Dataflow Modeling 的方式撰寫程式碼,因為程式碼相對簡短。而 Gate Level Modeling 需要使用的邏輯閘量在這個情況較多 (約為 7 個邏輯閘) ,因此不建議。
module Full_Adder(
input A, B, Cin,
output Sum, Cout
);
assign Sum = A ^ B ^ Cin;
assign Cout = (A & B) | (A & Cin) | (B & Cin);
endmodule
再來,我們可以透過 Full_Adder 實作 Adder4 (四位元加法器)。
加法器的實作方式其實很多種,其中,最簡單的叫做 Ripple Carry Adder ,意思是下一個加法器的 Carry In 會取決於上一個加法器的 Carry Out 。這種加法器是我們直覺上最能理解的設計,也是我們實作四位元加法器的參考。可以參考附圖 。 (圖片來源:維基百科)
如果考慮效能,Carry Lookahead Adder (CLA) 也是一個不錯的選擇,會較 Ripple Carry Adder 快上不少。因為 CLA 可以提前知道加法器的 Carry In ,如此就可以以較快的時間完成一樣的事情。
下方的程式碼中,我們除了使用 Full_Adder 模組,還宣告了 Ctemp 的變數。
原因是我們在上面提到 Ripple Carry Adder 必須透過上一個加法器的 Carry Out 來決定 Carry In ,我們必須提供一些空間作為他們的跳板,這就是 Ctemp 。
module Adder4(
input [3:0] A, B,
input Cin,
output [3:0] Sum,
output Cout
);
wire [3:1] Ctemp;
Full_Adder F0(A[0], B[0], Cin, Sum[0], Ctemp[1]);
Full_Adder F1(A[1], B[1], Ctemp[1], Sum[1], Ctemp[2]);
Full_Adder F2(A[2], B[2], Ctemp[2], Sum[2], Ctemp[3]);
Full_Adder F3(A[3], B[3], Ctemp[3], Sum[3], Cout);
endmodule
這個模組會有三個部分要處理:
參數的名稱可以參考 BCD 加法器的電路圖,以下說明自定義的參數:
Cout0: 第一個加法器的進位,參與決定 Cout 的訊號
Cout1: 第二個加法器的進位,無意義,僅僅是為了配合模組所訂定的參數數量。
wire [3:0] Z 的數值,因為 Z 相對整個模組只是個中間值,所以要另外宣告使用。module BCD_Adder(
input [3:0] A, B,
input C,
output [3:0] Sum,
output Cout
);
wire [3:0] Z;
wire Cout0, Cout1;
Adder4 A0(A, B, C, Z, Cout0);
assign Cout = Cout0 | (Z[3] & Z[2]) | (Z[3] & Z[1]);
Adder4 A1 (Z, {1'b0, {2{Cout}}, 1'b0}, 1'b0, Sum, Cout1);
endmodule
