破題

首先，我們知道二元搜尋樹的一個重要特性是其中序走訪結果為遞增序列。因此，如果我們得到一個遞增陣列，我們可以確定這個陣列可以作為某個二元搜尋樹的中序走訪結果。

然而，僅憑中序走訪結果，我們並不能確定一棵唯一的二元搜尋樹。原因是在不考慮樹的高度平衡的情況下，任何數字都可以作為二元搜尋樹的根節點。因此，對於同一個中序走訪結果，可能存在多種不同的二元搜尋樹。

以下二元搜尋樹的中序走訪結果均為 [-10, -3, 0, 5, 9]

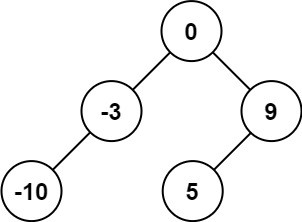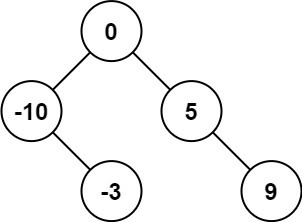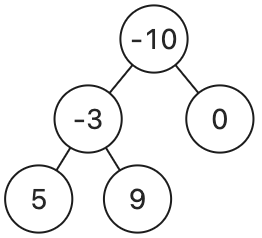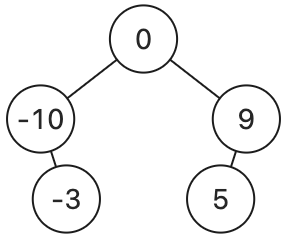即使我們增加了一個限制條件，要求二元搜尋樹的高度平衡，我們仍然無法確定一棵唯一的二元搜尋樹。這是因為對於同一個中序走訪結果，可能存在多種不同的高度平衡的二元搜尋樹。

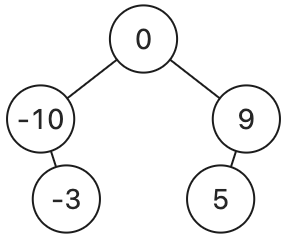
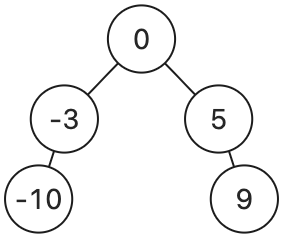
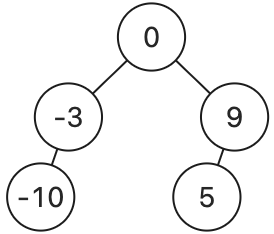
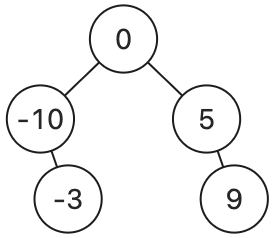
以下二元搜尋樹的中序走訪結果均為 [-10, -3, 0, 5, 9]

我們可以直觀地想到，選擇陣列裡的中間數字作為二元搜尋樹的根節點，這樣可以確保左右子樹的節點數量相同或者最多相差 ，從而使得樹保持平衡。如果陣列的長度是奇數，那麼根節點的選擇是唯一的。但是，如果陣列的長度是偶數，我們可以選擇中間位置左邊的數字或者右邊的數字作為根節點。選擇不同的根節點會長出不同的平衡二元搜尋樹。

在確定平衡二元搜尋樹的根節點後，剩下的數字將被分配到左子樹和右子樹中。由於左子樹和右子樹也都是平衡二元搜尋樹，我們可以使用遞迴的方法來長出整棵平衡二元搜尋樹。

當然，這只是我們直觀的想法。那麼，為什麼這樣建樹一定能保證是「平衡」的呢？可以參考「1382. Balance a Binary Search Tree」這道題目，它的構造和方法和本題完全相同。感興趣的同學，可以去了解一下。

遞迴的 base case 是當二元搜尋樹不包含任何數字，也就是說，當二元搜尋樹為空時，我們就達到了遞迴的 base case。

在給定中序排序陣列的情況下，我們可以確定每一個子樹中的數字在陣列中一定是連續的。因此，我們可以通過標記陣列範圍來確定子樹包含的數字。我們將這個標記範圍記為 。對於整個中序排序陣列，標記範圍從 到 。當 時，表示平衡二元搜尋樹為空。

這道題目有幾種不同的策略。像是是總是選擇陣列中間位置左邊的數字作為根節點；或是總是選擇陣列中間位置右邊的數字作為根節點；或者，可以選擇任意一個中間位置的數字作為根節點。

別閉門造車，一起準備面試吧！
在紙上呈現100%完美的你！打爆天下無敵手的履歷怎麼寫？找工作前的第一步：履歷健檢！
我們將幫助您撰寫一份出色的履歷表，讓您在眾多求職者中脫穎而出。我們將為您提供專業的建議和指導，幫助您在履歷上呈現最完美的自己。如果心動的話，就別猶豫啦！趕快把握機會，動動手指投遞履歷吧！立即加入 Line 讀書會，和大家一起實現夢想！

履歷諮詢	加入讀書會 (邀請碼：3344)

中序走訪

解題思路

如果我們選擇陣列中間位置左邊的數字作為根節點，那麼根節點的 index 可以用公式 來計算。這裡的除法是整數除法，也就是說，結果會取 floor。

總是選擇陣列中間位置左邊的數字作為根節點 [-10, -3, 0, 5, 9]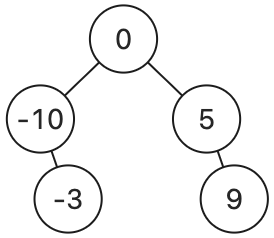

程式

import kotlin.math.ceil
import kotlin.math.log
import kotlin.math.pow

class Solution {
    fun sortedArrayToBST(nums: IntArray): TreeNode? {
        return buildTree(nums.toList())
    }

    private fun buildTree(arr: List<Int>): TreeNode? {
        val h = ceil(log(arr.size.toDouble(), 2.0)).toInt()
        return if (h == 0) TreeNode(arr[0])
        else {
            val rootIndex = arr.size / 2
            val left = if (rootIndex > 0) buildTree(arr.take(rootIndex)) else null
            val right = if (arr.size - 1 - rootIndex > 0) buildTree(arr.takeLast(arr.size - 1 - rootIndex)) else null
            TreeNode(arr[rootIndex]).apply {
                this.left = left
                this.right = right
            }
        }
    }
}

複雜度分析

• 時間複雜度:
  ，其中 是陣列的長度。這是因為我們需要遍歷整個陣列，並且每個數字只會被訪問一次。

• 空間複雜度:
  ，其中 是陣列的長度。這裡的空間複雜度不考慮回傳值所占用的空間。空間複雜度主要取決於遞迴堆疊的深度，而遞迴堆疊的深度是 。

　更多演算法題解，一起來學習！

別閉門造車，一起準備面試吧！

在紙上呈現100%完美的你！打爆天下無敵手的履歷怎麼寫？找工作前的第一步：履歷健檢！

履歷諮詢	加入讀書會 (邀請碼：3344)