動態規劃 (DP)

解題思路

最長共同子序列問題是典型的二維動態規劃問題。例如，給定兩個字串 text1 = "abcde" 和 text2=“ace”，我們要求它們的最長共同子序列的長度。我們可以用一個二維陣列 table 來記錄每一步的結果，其中 table[i][j] 表示 text1 的前 i 個字元和 text2 的前 j 個字元的最長共同子序列的長度。如下表所示：

我們可以從左上角開始填充 table 陣列，每次只考慮 text1 的一個字元和 text2 的一個字元。我們可以用以下公式來更新 table[i][j] 的值：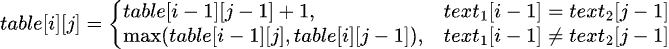

這個公式的含義是：

• 如果 或 ，表示其中一個字串為空，那麼它們的最長共同子序列的長度為零
• 如果 ，表示目前比較的兩個字元相同，那麼它們可以在之前的最長共同子序列的基礎上增加一個字元，並構成一個共同子序列
• 如果 ，表示目前比較的兩個字元不同，那麼它們不能同時出現在最長共同子序列中，我們需要從兩種可能的情況中選擇一種，即忽略 text1 的目前字元或忽略 text2 的目前字元，並取較大的值作為 table[i][j] 的值

最終計算得到 table[m][n] 即為 text1 和 text2 的最長共同子序列的長度，如上表中的 3。

跟一流的人才幹大事，享受成功進步的高級樂趣！
內推機會來啦！能與優秀的程式設計師共事，是特別痛快的事，因為厲害的工程師大神會刺激你想要迎頭趕上的上進心，尤其是一起討論解決方案時，他們會觸發你有更好的解決思維能力，彼此共同成長並且一起享受解謎與破關般的樂趣。 你一定聽得懂我在說甚麼感覺，趕快把握機會，動動手指投遞履歷吧！ 立即加入「面試讀書會」，和大家一起準備面試！

內推機會	加入讀書會 (邀請碼：8741)

程式

import kotlin.math.max

class Solution {
    fun longestCommonSubsequence(text1: String, text2: String): Int {
             val table = Array(text1.length + 1) {
            IntArray(text2.length + 1) {
                0
            }
        }
        for (i in text1.indices) {
            for (j in text2.indices) {
                val row = i + 1
                val col = j + 1
                if (text1[i] == text2[j]) {
                    table[row][col] = table[row - 1][col - 1] + 1
                } else {
                    table[row][col] = max(table[row - 1][col], table[row][col - 1])
                }
            }
        }
        return table[text1.length][text2.length]
    }
}

複雜度分析

對於這個問題，我們假設兩個字串 text1 和 text2 的長度分別是 和 。我們宣告了一個二維陣列 table 來記錄每一步的結果，它有 m+1 列和 n+1 行（因為要考慮空字串的情況）。

• 時間複雜度:
  ，因為我們需要對 table 陣列中的每個元素進行計算，而 table 陣列中有 個元素（相當於 table 陣列的大小）。

• 空間複雜度:
  ，因為我們需要宣告一個大小為 的二維陣列 table 來存儲每一步的結果。

　更多 LeetCode 解答在此，一起來學習！

內推機會來啦！

跟一流的人才幹大事，享受成功進步的高級樂趣！

內推機會	加入讀書會 (邀請碼：8741)