[QPE] Iterative QPE

2023 iThome 鐵人賽

DAY 3

自我挑戰組

不嚴謹的量子計算雜談系列第 3 篇

15th鐵人賽量子計算

bwl

2023-09-12 08:57:42

311 瀏覽

分享至

[QPE] Iterative QPE

昨天認識的 QPE with QFT 雖然概念上十分簡潔，但在現有的量子電腦上難以實現。今天要介紹的 QPE 演算法基於用時間換空間的概念，來減少 quantum register 的大小，並稍微減輕了電路深度造成的負擔。

Iterative QPE，顧名思義就是透過迭代來計算出我們感興趣的 phase $\theta$ 。對於任意在 $[0, 1$ ) 之間的 phase $\theta$ ，我們可以將她以二進位表示：(假設 $\theta$ 可以 $d$ 位元表示)

$\theta = 0.\theta_1\theta_2\cdots\theta_d$

所謂迭代，就是一次算出一個 bit！

根據昨天的定義， $U|u\rangle = \exp(2\pi i\theta)|u\rangle$ ，也就是說

$U^{2^j}|u\rangle = \exp(2\pi i\theta\cdot 2^j)|u\rangle = \exp(2\pi i \cdot 0.\theta_{j+1}\cdots\theta_{d})|u\rangle.$

具體而言，

$U^{2^{d-1}}|u\rangle = \exp(2\pi i \cdot 0.\theta_d)|u\rangle.$

即使如此，要怎麼得到 $\theta_d$ 的資訊呢？看看電路圖會更有感覺：(我圖沒畫好所以線斷掉了，請見諒😅)

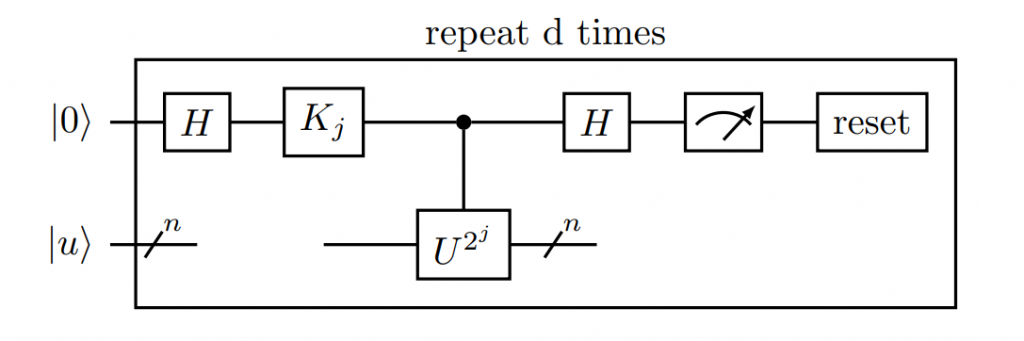
其中 $K$ 是某些旋轉閘的代稱 (等等會說明 $K$ 是什麼)。為了要清楚了解上述電路代表的意義，我們來算算看經過一次上圖方框內的運算，可以得到什麼樣的量子態吧！(令 $j=d-1$ ；此時 $K=I$ ，也就是單位矩陣)

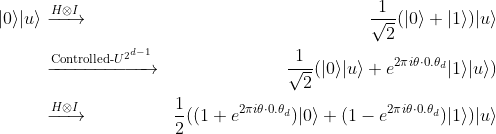
此時測量第一個 qubit 而結果為 $|1\rangle$ 的機率是

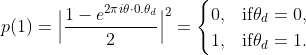
於是我們可以透過測量到 $|1\rangle$ 的機率來獲取 $\theta_d$ 的資訊！但是，當 $j \not = d-1$ 該怎麼辦？如果 $j=d-2$ ，

$U^{2^{d-2}}|u\rangle = \exp(2\pi i\cdot 0.\theta_{d-1}\theta_d)|u\rangle.$

若可以想辦法將 $\exp(2\pi i\cdot 0.\theta_{d-1}\theta_d)$ 中的 $\theta_d$ 去掉，問題就圓滿解決了；沒錯！ $K$ 現在派上用場了！本質上， $K$ 的功能正是將已經算過的 phase 資訊從目前的迭代中去除。具體而言， $K$ 可以如下表示：

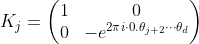
換句話說， $K$ 是根據已知 phase 資訊的反向旋轉閘！

這樣的計算過程牽涉到：根據測量到的 classical bit 決定旋轉角度。如果使用 Qiskit 實作，我們可以使用如下的語法

# qc: QuantumCircuit 物件
# c0: qc 內的一個 classical bit，儲存當前測量資訊
# q0: qc 內的一個 qubit，等同上圖中第一個 qubit
##### 如果 c0 儲存的測量結果為 1，將 q0 旋轉 -pi/2 #####
with qc.if_test((c0, 1)):
	qc.p(-math.pi/2, q0)

完整的 IQPE 實作請見 IBM Quantum Challenge Spring 2023！