[QSP / QSVT] QSVT 實作：基本框架

2023 iThome 鐵人賽

DAY 19

自我挑戰組

不嚴謹的量子計算雜談系列第 19 篇

15th鐵人賽量子計算

bwl

2023-09-28 09:23:43

239 瀏覽

分享至

今天來看看 QSVT 的基本框架實作，我們使用的是 Qiskit；完整的程式碼在這裡！

首先，我們定義函式 QSVT(...)，其接受的參數有：

A：QSVT 的目標矩陣
phi_seq：角度序列；我們預設角度慣例 (convention) 是 R，以符合 QSVT 文獻。如果輸入慣例是 Wx 或 Wz，我們需要先轉換慣例。
- convention = R：指定慣例 (預設是 R)
real_only = True：當我們以多項式 $P$ 逼近任意實函數 $f$ 時，為了有效率地計算出 $P$ 同時又滿足定理需求 (關於多項式的限制，我們在幾天前的定理沒有談到)，經常 $P$ 的實部可以確實逼近 $f$ ，但 $P$ 的虛部卻是雜亂的。因此我們希望「只取」 $P$ 的實部，並設法將 $P$ 的虛部抵銷。換句話說我們需要：

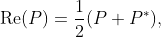
其中 $\text{Re}(P)$ 是 $P$ 的實部且 $P^*$ 是 $P$ 的複共軛。將 real_only 設為 True 代表我們希望擺脫 phi_seq 所對應的多項式虛部。

在 QSVT 中，我們的操作對象是 A 的 block-encoding U。一個具體的 block-encoding 策略是：

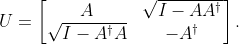
其直截了當的實作方法是：

def block_encode(A: np.ndarray) -> np.ndarray:
    n = A.shape[0]
    A_dag = np.conjugate(np.transpose(A))
    
    I_AAd = np.identity(n) - A @ A_dag 
    eigval, eigvec = np.linalg.eig(I_AAd)
    sq_I_AAd = eigvec * np.sqrt(eigval) @ np.linalg.inv(eigvec)

    I_AdA = np.identity(n) - A_dag @ A
    eigval, eigvec = np.linalg.eig(I_AdA)
    sq_I_AdA = eigvec * np.sqrt(eigval) @ np.linalg.inv(eigvec)

    U = np.zeros(shape=(2 * n, 2 * n), dtype=complex)
    U[0:n, 0:n] = A
    U[0:n, n:] = sq_I_AAd
    U[n:, 0:n] = sq_I_AdA
    U[n:, n:] = -A_dag
    
    return U

接著，我們要處理角度序列的慣例。底下實作了從 Wx 轉換至 R 的方法 (據此處 Corollary 8)：

def convert_convention(Wx_seq: list) -> tuple:
    R_seq = np.zeros(len(Wx_seq))
    
    # 這裡的 d 正是 QSVT 定理中的 d
    d = len(Wx_seq) - 1 
    
    # R-convention 的序列長度比 Wx-convention 的長度少 1 (R_seq[0] 用不到)
    R_seq[1] = Wx_seq[0] + Wx_seq[d] + (d - 1) * np.pi / 2
    for j in range(2, d + 1):
        R_seq[j] = Wx_seq[j - 1] - np.pi / 2
    return (d, R_seq)

還有一個很重要的部分是，如何實作「對 $\Pi$ 所投影到的空間進行 phase shift」？如下圖所示 (圖來源：A Grand Unification of Quantum Algorithms)：

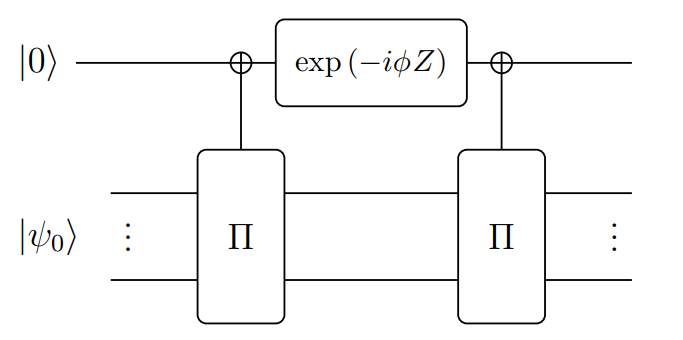
具體而言，若 $\Pi = |11\rangle\langle 11|$ ，則

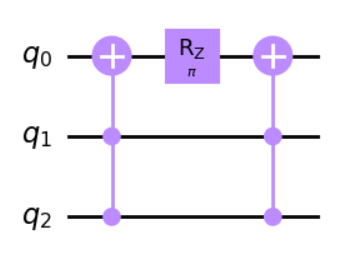
不過呢，由於我們 QSVT 的 $\Pi = |0\rangle\langle 0|\otimes I$ 相當簡單，因此我們只需要 CNOT：(假設 q1 是用來 block-encode A 的 qubit，而 q2 和 q3 則是 A 本身)

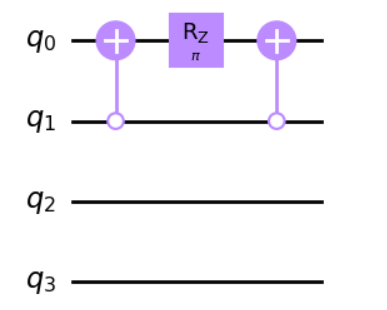
程式實作類似於底下這段：

from qiskit import QuantumCircuit

qc = QuantumCircuit(4)

...

qc.cx(control_qubit=1, target_qubit=0, ctrl_state=0)
qc.rz(phi=phi_s, qubit=0)
qc.cx(control_qubit=1, target_qubit=0, ctrl_state=0)

而此電路還可以進一步簡化：將輔助 qubit q0 省去！(但若要實作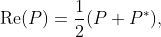，我們需要 LCU 的想法 (昨天稍有提到)，此時 q0 就是必須的)

QSVT 基本框架的實作告一段落了，明天來實作 QSVT 的應用！

不嚴謹的量子計算雜談系列第 19 篇