五天前我們談到了基於 QSVT 的 QPE 演算法，看起來頗複雜，而複雜的電路帶來的效益是：估計的 phase 可以更準確 (在某些噪音之下)。但是今天，我們來看看這樣的 QPE 演算法可以如何簡化，並且簡化之後和最初三種 QPE 又有什麼關聯！

假設我們要估計的 phase 能以 位元表示。下圖是基於 QSVT 的 QPE 演算法電路圖：(圖一)

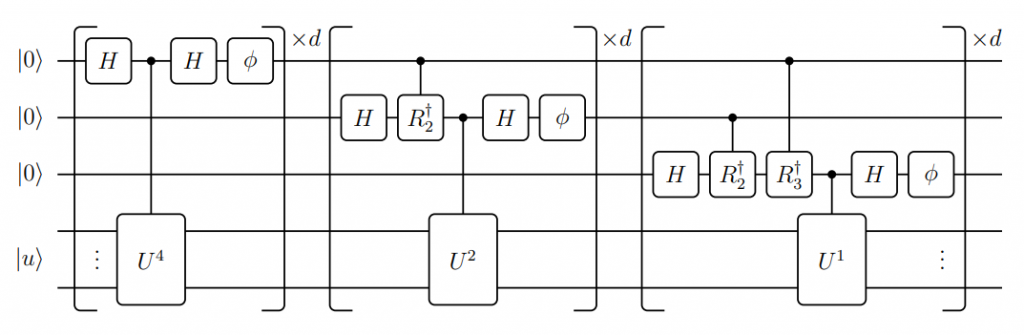
如果我們令角度序列長度 ，且令該唯一的角度 ，我們可以得到如下的簡化電路：(圖二)

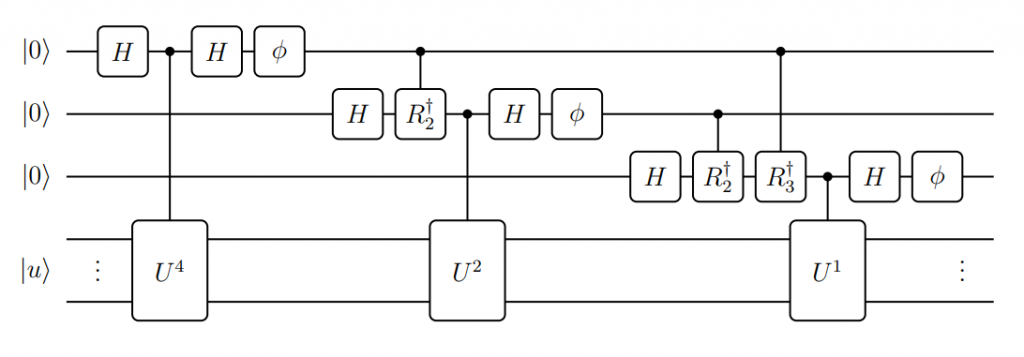
經過一些量子閘的交換 (他們確實滿足交換律)，我們得到：(圖三)

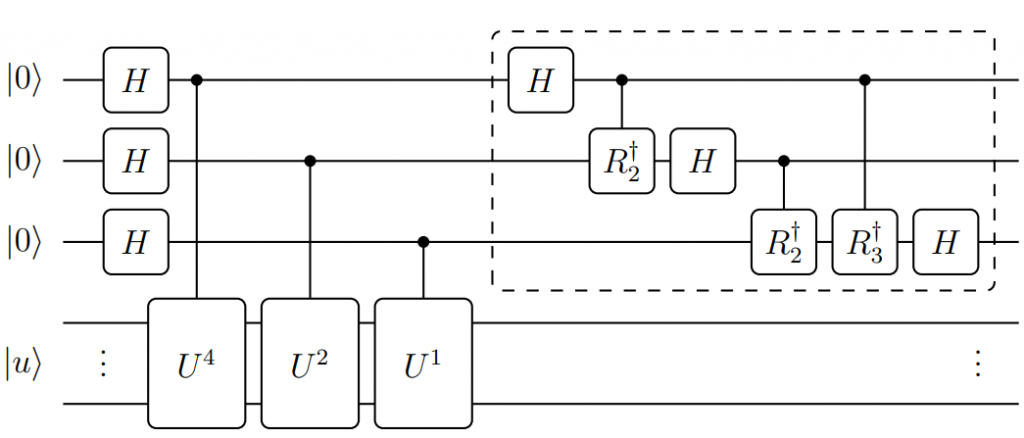
發現了嗎？圖右方虛線框起來的區域正是 Inverse QFT，而整體電路就是有 QFT 的 QPE！也就是說，如果我們將 QSVT 做極大程度的化簡，便能「重新發現」有 QFT 的 QPE！

讀到這裡，各位可能在想：這樣的簡化有什麼意義？筆者認為，基於 QSVT 的 QPE 方法稍嫌太複雜 (不論概念或實作)。不過呢，這個方法雖沒有提供更有效的 QPE，但藉由化簡，它帶給我們的啟發是：用不同的眼光重新理解過去的 QPE 演算法；而化簡過程的精神在於：最小化 QSVT 的影響 (讓角度序列消失)，卻同時保持 QSVT 的樣貌 (圖二)！哎呀，說了這麼多，差點忘記今天的主題是實作了。馬上來看看吧！

def phase_estimation(
        U: np.ndarray, # 目標矩陣
        precision: int, # 精確到小數後幾位
        prepare_eigenvec: QuantumCircuit # 準備 eigenvector 的電路
) -> QuantumCircuit:    
    qr = QuantumRegister(precision + eigenvec_dim)
    qc = QuantumCircuit(qr)

    phase = qr[0:precision]
    eigenvec = qr[-eigenvec_dim:]

	# 準備 eigenvector
    qc.append(prepare_eigenvec, qargs=eigenvec)

    # 基於 QSVT 來實現有 QFT 的 QPE
    for j in range(precision - 1, -1, -1):
        bit = precision - 1 - j
        qc.h(phase[bit])
        
        # 用來取代「先測量再旋轉」的 controlled-旋轉
        for r in range(2, precision - j + 1):
            qc.cp(
                theta = -(2 * np.pi / (2 ** r)),
                control_qubit = phase[bit - r + 1], 
                target_qubit = phase[bit]
            )

        U_gate = UnitaryGate(data=U**(2**j), label=f'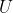![](https://latex.codecogs.com/png.image?U)^{2**j}').control(num_ctrl_qubits=1)
        if eigenvec_dim == 1:
            qc.append(U_gate, [phase[bit], eigenvec])
        else:
            qc.append(U_gate, [phase[bit], *eigenvec])
        qc.h(phase[bit])

        qc.barrier()

    return qc

假設我們有一矩陣

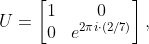
而我們希望可以估計出 phase 。於是我們利用上面定義的 phase_estimation(...)：

prepare_eigenvec = QuantumCircuit(1)
U = np.array([
    [1, 0],
    [0, np.e ** (2 * np.pi * 1j * (2/7))]
])
prepare_eigenvec.x([0])

# 我們希望精確到 6 位小數
precision = 6

qc = phase_estimation(U, precision, prepare_eigenvec)

並且在模擬器上執行：

from qiskit import transpile
from qiskit_aer import AerSimulator
from qiskit.visualization import plot_histogram

cr = ClassicalRegister(precision)
qc.add_register(cr)
qc.measure(list(range(precision)), cr)
sim = AerSimulator()
transpiled_circuit = transpile(qc, sim)

# run job
shots = 1000
job = sim.run(transpiled_circuit, shots=shots, dynamic=True)

# Get the results and display them
exp_result = job.result()
exp_counts = exp_result.get_counts()
plot_histogram(exp_counts)

我們得到測量結果：

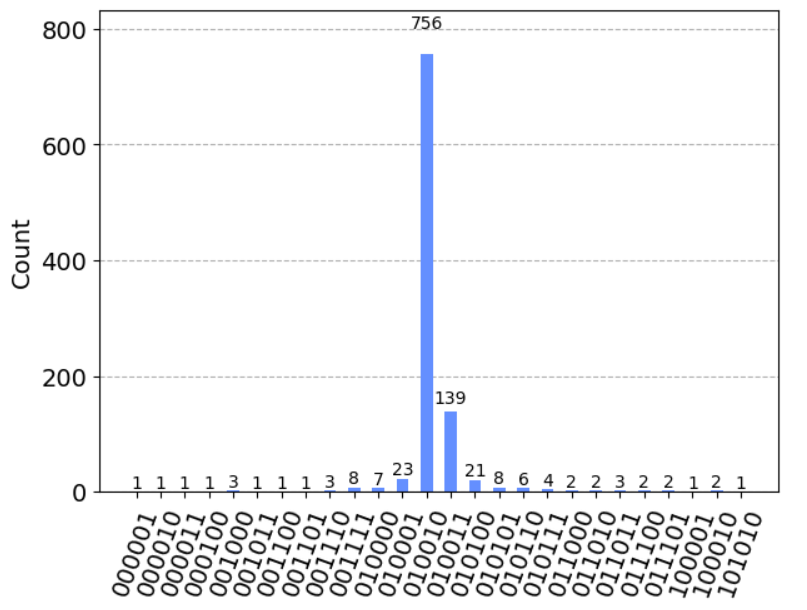
其中機率最高的結果是 010010，而 在二進位的小數後六位元正是 010010！

參考資料

• A Grand Unification of Quantum Algorithms
  • 圖一、圖二和圖三的來源