在寫程式時，有時會遇到無法單純使用迴圈解決的問題，這時候就會需要使用函式的「遞迴」功能，透過遞迴的方式，就能處理每次重複需要改變的參數或輸出結果，這篇教學將會介紹 Python 函式裡的遞迴。

原文參考：遞迴 recursion

本篇使用的 Python 版本為 3.7.12，所有範例可使用 Google Colab 實作，不用安裝任何軟體 ( 參考：使用 Google Colab )

什麼是遞迴？

當「一個函式會在執行當中，不斷地自己呼叫自己」，這個函式便具有「遞迴」的特性，遞迴的本質很像迴圈，但卻可以處理許多迴圈不容易處理的參數或回傳值，要撰寫一個有遞迴特性的函式，需要滿足下列兩個特徵：

• 函式會自己呼叫自己。
• 具備函式停止條件 ( 避免無窮盡的呼叫自己 )。

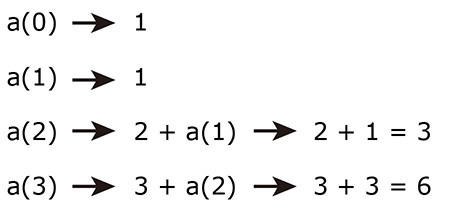
下方的程式碼表現了一個最基本的遞迴函式：

def a(n):                    # 建立函式 a，帶有參數 n
    if n == 0 or n == 1:     # 如果 n 等於 0 或 1
        return 1             # 回傳結果 1
    else:
        return n + a(n-1)    # 使用遞迴

print(a(3))                  # 執行結果為 6 ( 3+2+1 )

下圖表現上述遞迴程式碼的執行的順序：

使用遞迴函式的注意事項

遞迴雖然很方便，但在使用上仍有下列幾點需要注意：

• 遞迴雖然有時可以減少複雜度，但相對會使用更多的記憶體。
• Python 將遞迴呼叫次數限制設定為 3000 次，超過就會發生錯誤，被強制停止。

使用遞迴 vs 使用迭代操作

n 階層

數字 n 階層 (n!) 的定義為：(n) x (n-1) x (n-2)....x2 x1，可以使用下方遞迴方式處理：

def a(n):                    # 建立函式 a，帶有參數 n
    if n == 0 or n == 1:     # 如果 n 等於 0 或 1
        return 1             # 回傳結果 1
    else:
        return n * a(n-1)    # 使用遞迴
print(a(4))                  # 執行結果為 24 ( 4x3x2x1 )

下圖為遞迴程式碼的執行的順序：

費波那契數列

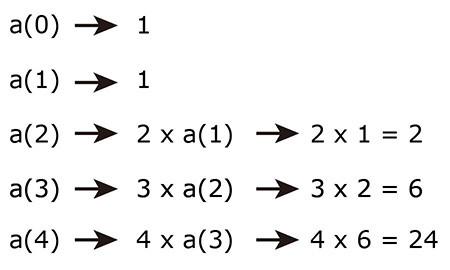
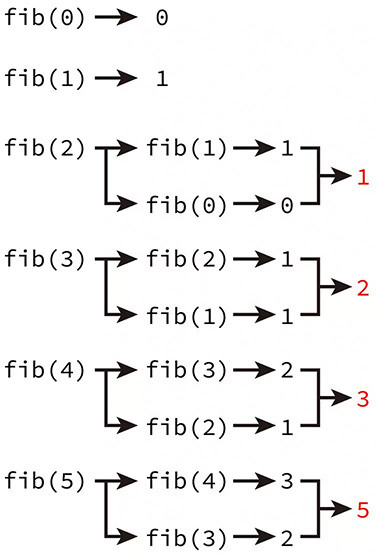
下方的程式碼，使用遞迴的方式來建立費波那契數列。

def fib(n):                         # 建立函式 fib，帶有參數 n
    if n > 1:                       # 如果 n 大於 1
        return fib(n-1) + fib(n-2)  # 使用遞迴
    return n
for i in range(20):                 # 產生 20 個數字
    print(fib(i), end = ',')        # 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181

下圖為遞迴程式碼的執行的順序：

最大公因數

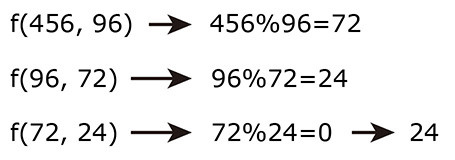
下方的程式碼，使用遞迴的方式，搭配「輾轉相除法」來找出兩個數字的最大公因數。

def f(a, b):             # 建立函式 f，帶有參數 a 和 b
    if a%b == 0:         # 如果相除餘數為 0，回傳結果
        return b
    else:                # 如果相除不為 0，表示還沒找到最大公因數
        return f(b, a%b) # 使用遞迴，參數 a 使用 b，b 使用 a 除以 b 的餘數
print(f(456, 48))        # 得到結果 24

下圖為遞迴程式碼的執行的順序：

更多教學

大家好，我是 OXXO，是個即將邁入中年的斜槓青年，我有個超過一千篇教學的 STEAM 教育學習網，有興趣可以參考下方連結呦～ ^_^

• Python 教學 ( 學習導讀 )
• Scratch 教學
• GA4 ( Google Analytics 4 ) 教學
• 生成式 AI ( AIGC ) 教學
• Midjourney 教學
• HTML 教學