這邊直接濃縮Arrays 101 三個小節的內容，有關陣列的基本操作不外乎是新增、刪除和搜尋這三種(當然還有排序，但這邊沒特別講)，這些在前一篇有大致操作過一遍了，在這一篇會比較詳細地解釋，下面會直接使用上一篇建立的int[] intArray = new int[5];繼續講解，不知道的話可以先看上一篇。

新增

新增這個小節中，Explore 展示了三種新增的情境：

1. 在陣列的尾端新增元素。
2. 在陣列的開頭新增元素。
3. 在陣列中間的任何位置新增元素。

在陣列的尾端新增元素

這其實沒甚麼好解釋的，就是像下圖示意的一樣，在尾端新增元素。

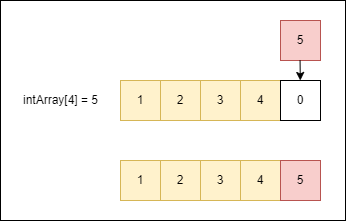
不過，沒這麼快就結束，仔細一點思考的話，尾端的意思是指還沒指定元素值的最前端，像下圖示意的一樣，在還未指定最後兩個元素值時，這樣intArray[3]也算是尾端。

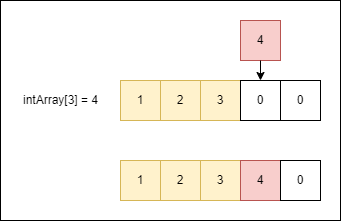
只看到這邊可能會以為這有什麼好講的，不不不，注意元素的索引位置可有意思了。

在陣列的開頭新增元素

可能有些人會以為是直接intArray[0]=10，把指定元素值進去第一個索引位置，但這是替換第一個元素值而不是在開頭新增元素，真正的在開頭新增元素有兩個步驟：

1. 將每個元素值往後移動一個索引位置。
2. 將指定元素值放入第一個索引位置。

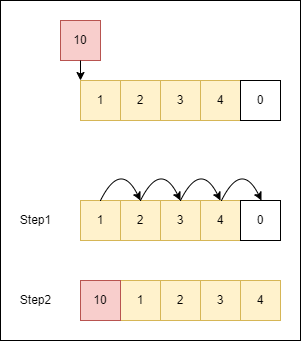
從上圖可以知道，要在開頭新增元素是非常消耗時間的操作，需要將每個元素往後移動，而且這不是有固定時長的操作，你的陣列長度是多少就要移動多少個元素，以時間複雜度分析來看的話，它是一個線性時間複雜度O(n)，n 是陣列的長度。

在陣列中間的任何位置新增元素

和在陣列開頭新增元素類似，想在陣列中間的任何位置新增元素，都需要將那個位置後方的所有元素值往後移動一個索引位置，這邊就不再贅述，畫個圖示意一下。

刪除

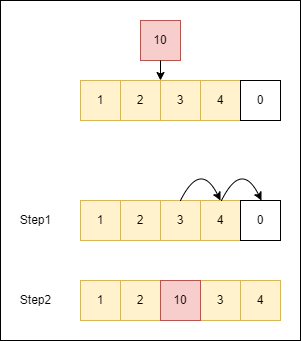
看到這邊才注意到前面提到的陣列長度的意義，當使用陣列進行操作時，可以另外加上一個變數length 紀錄陣列長度，用來標示目前陣列儲存的元素數量，新增和刪除操作的依據也是這個length 變數。

int[] intArray = new int[5];
int length = 0;

for (int i = 0; i < 3; i++) {
	intArray[i] = i;
	length++;
}

// intArray: 1, 2, 3, 0, 0
// length: 3

// 刪除最後一個元素
length--;

刪除最後一個元素

這邊就體現了length 這個變數的用處，還記得創建陣列的時候會直接在記憶體挖一個相鄰的區塊儲存元素嗎？

正因為已經挖好了一個區塊，不管它裡面是預設值0 或null 還是已經指定元素值，都改變不了它已經有個區塊的事實；而我們使用length 紀錄陣列的長度，目的是要在陣列的尾端新增元素時，可以透過它知道應該新增在哪個位置，而刪除陣列尾端的資料就只需要將其減一即可。

刪除第一個元素

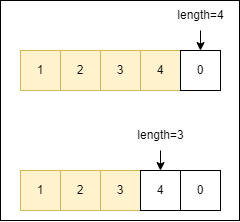
這部分就跟在陣列的開頭新增元素相反，新增的 時候是全部往後移動，刪除的時候則是往前覆蓋，並且length 減一。

刪除陣列中間的任何位置元素

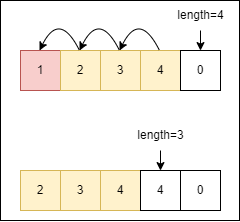
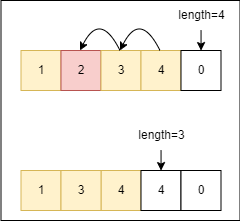
這部份也是跟在陣列中間的任何位置新增元素相反，新增的時候是索引位置之後的元素往後移動，刪除的時候則是往前覆蓋，並且length 減一。

搜尋

演算法的存在是為了以最短的時間和最少的資源達成我們的目的，對於陣列的操作來說，最重要的演算法就是搜尋演算法和排序演算法，不過在Arrays 101 並沒有提到排序演算法，可能其他Explore Card 會有，這邊有提了兩個搜尋的方法，線性搜尋和二元搜尋。

線性搜尋

如果我們要在陣列當中搜尋一個元素，而這個陣列沒有經過排序，也不確定是否存在這個元素，最簡單的方法就是線性搜尋，從頭開始一個一個找起，就像下圖示意的一樣；如果我們要找7，會在第三個元素找到，如果我們要找20，會整個陣列看過一次才知道沒有這個元素。

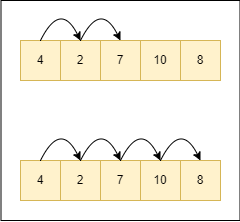
以程式碼來看的話，我會寫成像下面這樣：

int[] intArray = new int[] {4, 2, 7 ,10, 8};
int target = 7;

boolean exist = false;
for (int item: intArray) {
	if (item == target) {
		exist = true;
		break;
	}
}

System.out.println(exist);
// true

二元搜尋

二元搜尋法在之後的Explore Card 才會有詳細講解，Arrays 101 在這邊只大概提了一下，假設我們今天收到的陣列是已經排序好的，那就可以使用二元搜尋法，這會比線性搜尋法快很多。

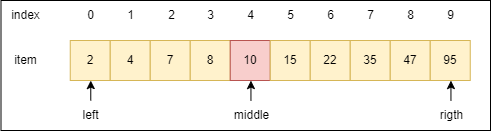
我們以上圖作為範例進行講解，當想要使用二元搜尋去取得22這個元素的索引值時，它的執行順序是這樣的：

1. 先設定搜尋的邊界(left 和right)，初始值是陣列的開頭和尾端。
2. 再來計算並取得中間值(middle)，如果是偶數則會是中間偏左。
3. 中間值和目標值比較，發現目標值介於middle 和right 之間。
4. 重新設定邊界位置(left 變為middle + 1)，再次計算中間值，再和目標值比較。
5. 重複上述動作，取得中間值→和目標值比較→改變邊界位置，直到取到目標值或邊界位置left>right。

這部分我不太會解釋，感覺寫的有點爛，還是直接看程式吧！

public static void main(String[] args) {
    int[] intArray = new int[] {2, 4, 7, 8, 10, 15, 22, 35, 47, 95};
    
    int target1 = 22;
    System.out.println(binarySearch(intArray, 0, intArray.length - 1, target1));
		// return 6
    
    int target2 = 200;
    System.out.println(binarySearch(intArray, 0, intArray.length - 1, target2));
		// return -1
}

private static int binarySearch(int[] intArray, int left, int right, int target) {
    if (left > right) return -1;

    int middle = (left + right) / 2;
    int midVal = intArray[middle];

    if (target > midVal) {
        return binarySearch(intArray, middle + 1, right, target);
    } else if (target < midVal) {
        return binarySearch(intArray, left, middle - 1, target);
    } else {
        return middle;
    }
}

LeetCode Problem

每個小節都有出兩道題目，感覺開始有點變化，需要稍微思考一下才解的出來，但一天以內還是解的完。

• 26. Remove Duplicates from Sorted Array
• 27. Remove Element
• 88. Merge Sorted Array
• 941. Valid Mountain Array
• 1089. Duplicate Zeros
• 1346. Check If N and Its Double Exist

小結

這一篇的篇幅應該也不算太長，主要是有很多圖片，內容也都只是基礎知識而已，不過二元搜尋法的講解感覺沒有寫很好，如果不清楚的話推薦這篇文章，它內容比較詳細也有展示動圖。

參考資料

Explore - LeetCode