遞迴的特徵是函式透過不斷呼叫自己，使問題變得越來越小，直到達到base condition停止，而解決問題。他常被用在divide and conquer, greedy algorithm 和 dynamic programming裡。在遞迴發生時，會將小問題存在stack memory(stack先進後出的資料結構，忘記的話可以回去複習一下)，看下面這個例子可能會比較清楚，導致其在記憶體的使用上，比iteration的方法不論在時間和空間上都來得沒效率:

# 在這個例子裡，其時間複雜度O(n^2)，空間複雜度O(n)
def Fab(n):
    #base condition:這個超級重要，沒有它遞迴會無限循環 
    if n in [0,1]:
        return num
    # 這裡把問題變成小問題來看
    else:
        return Fab(n-1)+Fab(n-2)
Fab(3)

Fab(3)=Fab(2)+Fab(1)
Fab(2)=Fab(1)+Fab(0)
Fab(1)=1
Fab(0)=0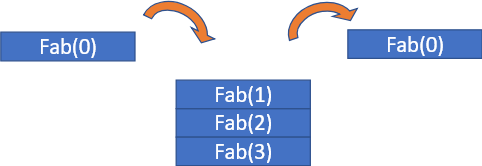

在這個例子裡，資料要在記憶體一直堆疊到base condition Fab(0)=0 and Fab(1)=1，才開始返回計算結果，故空間複雜度O(n)。而每一次函式都會呼叫自己兩次，因此會形成一個指數級的遞迴樹，故時間複雜度O(n^2)。

下面我們再看幾個例子:

# 題目是想知道一個數字的數字元總和是多少
# 時間複雜度: O(logn)，空間複雜度: O(logn)
def digitsum(n):
    if n==0:
        return 0
    else:
        return n%10+digitsum(n//10)
    
print(digitsum(106))
>> 7

#算最大公因數，b<a
時間複雜度:O(loga)，空間複雜度:O(loga)
def gcd(a,b):
    if a<0:
        a=-a
    if b<0:
        b=-b
    if b==0:
        return a
    else:
        return gcd(b,a%b)
print(gcd(30,5))
>> 5

總而言之，有的時候有些程式用iteration的方式可能不是那麼容易被想到，這時候可以用遞迴的方式來處理這些問題，但因為遞迴使用更多的記憶體還有時間，如果時間和記憶體空間非常重要的時候，盡量避免使用遞迴。

參考資料:
本文主要為udemy課程: The Complete Data Structures and Algorithms Course in Python的學習筆記，有興趣的人可以自己上去看看。