Tree (樹)

樹狀結構(tree)是一個非線性、有階層關係(hierarchical relationship)、非循環的資料結構。每個節點有的參數為其本身的資料和他連接的子類別。在某些裝況下，使用樹的效率會較其他資料結構的效率高，其包含Binary Search Tree, AVL, Red Black Tree, Trie......等等。我們的檔案系統或者是DOM也都使用tree。我們先介紹一下關於樹的專有名詞。因為中文翻譯有點奇怪，專有名詞的部分就直接用英文表示。
Root: tree最上面的節點，其無parent。
Edge: parent node and child node間的連結
Leaf: 沒有child node的節點
Sibling: 有共同parent的children節點
Ancestor: 一個節點的祖先(parent node, grandparent node, great grandparent nodes 都算)
Depth of node: 從root 到某個節點的距離(節點深度)
Height of node: 從某個節點到其最深(最底)節點的距離(節點的高) (等等介紹AVL時會用到)
Depth of tree: root node 的深度
Height of tree: root node 的高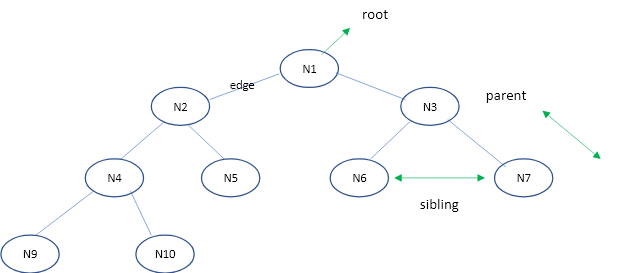

圖1. 在這個例子裡，N1為root，因此depth of tree=0, Height of tree=3。而其餘節點，像是N2，其depth=1, height=2。

Binary Tree (二元樹)

二元樹為一種樹狀資料結構，每個節點最多只有兩個子節點，通常簡稱為left child和right child。之後會要討論的Binary Search Tree, Heap Tree, AVL, red black trees, 和Syntax tree都屬於二元樹。二元樹有幾個專有名次分別為:
Full Binary Tree: 每個節點的子節點數不是0就是2。。
Perfect Binary Tree:除了葉子(leaf node) 外的所有節點都有兩個子節點。
Complete Binary Tree:樹裡每個節點的值由上到下，由左到右照順序排列。
Balanced Binary Tree: 每個節點，左右子樹的高不超過1。

這裡我先做幾個tree traversal(有系統的拜訪樹的每個節點一次)的介紹:
Traversal 可以分為Depth first search (深度優先)和breadth first search (寬度優先)，Depth first search 的例子又有preorder traversal, inorder traversal, and postorder traversal，下面我們分別介紹。

Depth first search (深度優先):
1. Preorder traversal: 拜訪節點的順序為root -> left subtree ->right subtree 。在圖2的例子中，拜訪節點的順序為N1-> N2 -> N4 -> N9 -> N10 -> N5 -> N3 -> N6 -> N7。
2. Inorder traversal: 拜訪節點的順序為left subtree -> root-> right subtree。在圖2的例子中，拜訪節點的順序為N9 -> N4 -> N10 -> N2 -> N5 -> N1 -> N6 -> N3 -> N7。
3. Postorder traversal: 拜訪節點的順序為left subtree -> right subtree -> root。在圖2的例子中，拜訪節點的順序為N9 -> N10 -> N4 -> N5 -> N2 -> N6 -> N7 -> N3 -> N1。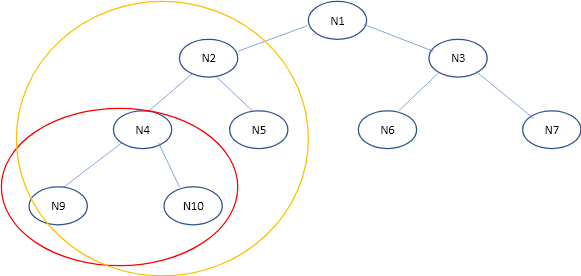

圖2. 在看tree traversal的時候，將subtree圈起來會更容易理解。

Breadth first search(廣度優先):
1. Level order traversal: 拜訪節點的順序為level by level，在圖3的例子中，拜訪節點的順序為N1 -> N2 -> N3 -> N4 -> N5 -> N6 -> N7 -> N9 -> N10。(level1->level2->level3->level4)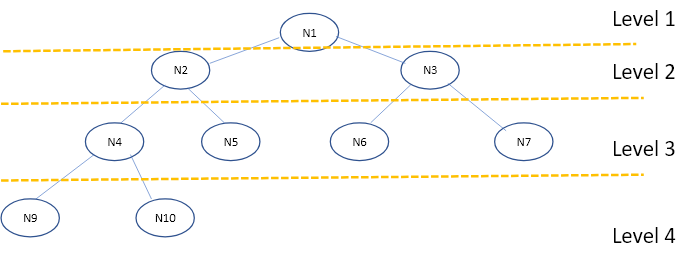

圖 3. Level order traversal 為廣度優先的traversal方法，每層由左到右拜訪每個節點。

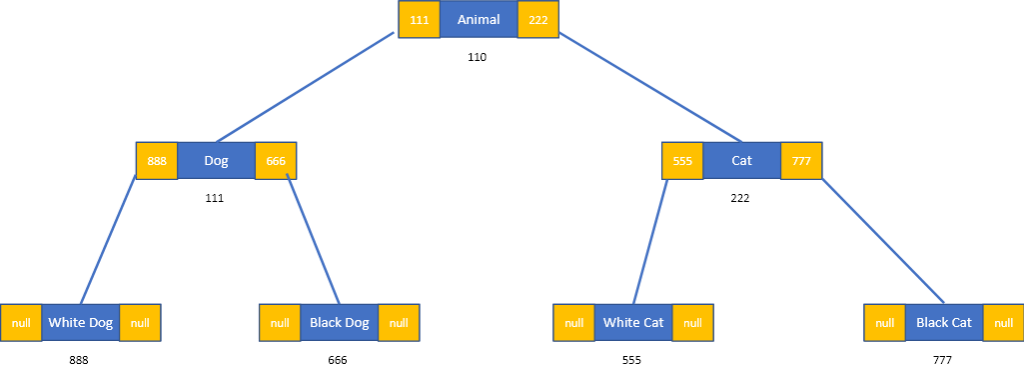
圖 4.用doubly linked list 二元樹。

到這裡先讓大家消化一下，明天再來帶大家分別用linked list和python list demo。

參考資料:
本文主要為udemy課程: The Complete Data Structures and Algorithms Course in Python的學習筆記，有興趣的人可以自己上去看看。