大家好，今天要來介紹的主題是stack。stack是一個相對簡單的主題，但是重點是何時使用stack。

Leetcode 84. Largest Rectangle in Histogram

這題是今天最難的題目，但是如果能夠解出來，這個主題基本上就能夠輕易的攻略的了。

題目敘述：input array是一連串的長條圖的高度，找出可以形成最大面積的長方形。

Example: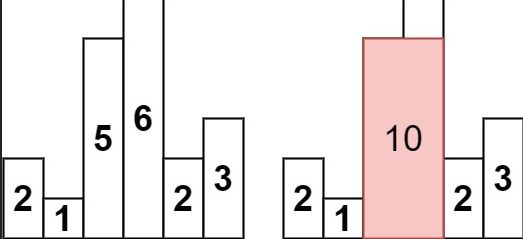

（圖源：leetcode）

圖中左邊是input，右邊是顯示最大的長方形的面積。

Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

分析：
如果今天圖長這樣：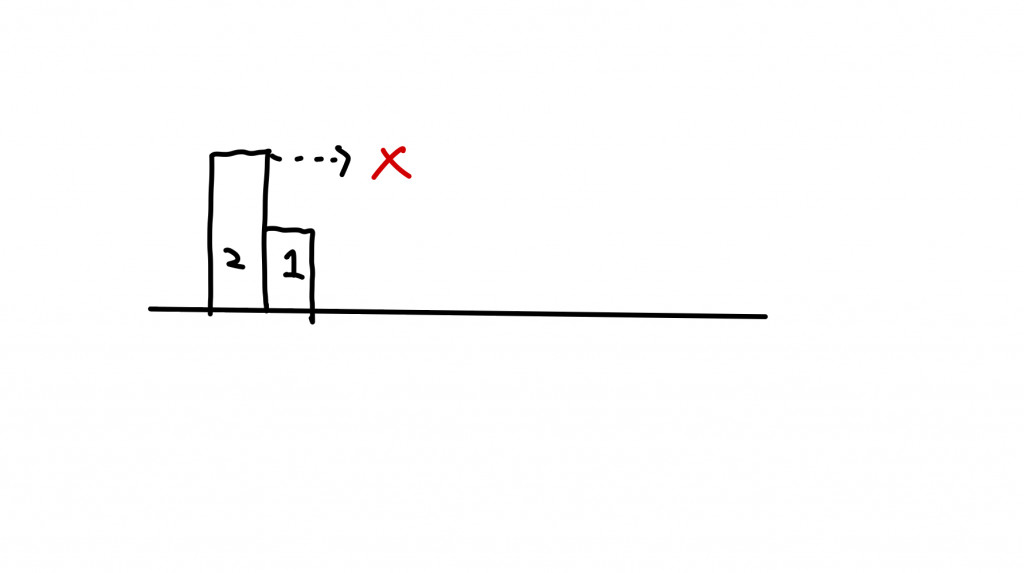

第一個長條比第二個高，也就是說第一個長條不能繼續以他的高度繼續延伸長方形的面積了，這時候就應該捨去他。

再看這個情況：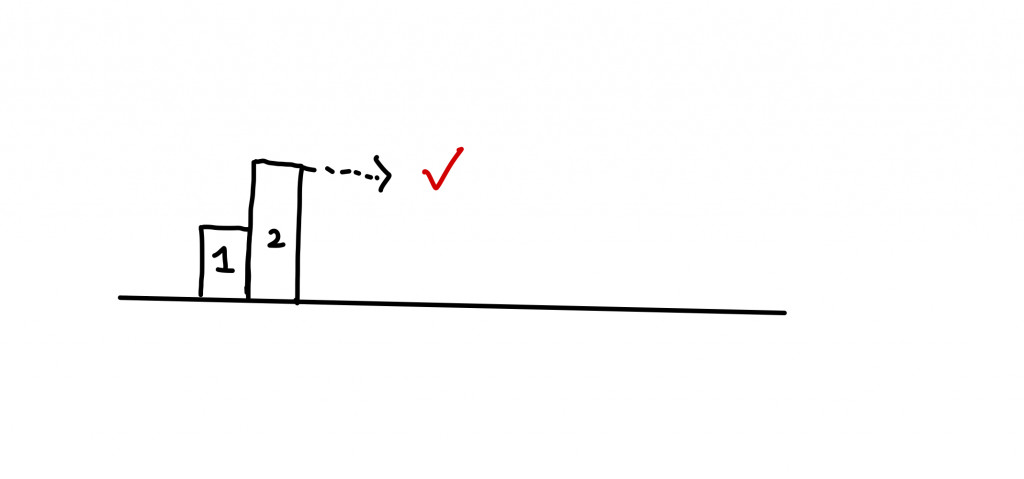

不管是第一個長條還是第二個長條都能繼續延伸下去，所以我們保存他們。

根據上述的討論，可以發現如果後來的長條比較短就要把前面比他都長的長條捨棄掉；但是如果比他短就保存這個長條，這種情況我們就可以利用stack來存取。

另外，當目前的長條比之前的矮，那麼他就可以「往前延伸」他的長方形。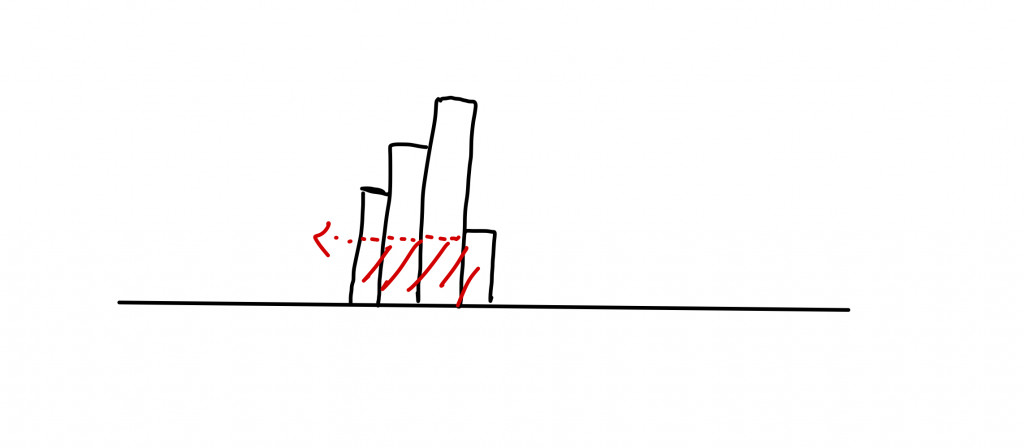

所以stack裡面要存放的是(index, height)這種tuple。index由是否可往前延伸來決定。
最後stack會保留呈現遞增高度的長條，我們需要去確認這些長條和他們延伸的寬度所構成的面積，是否會需要去更新最大面積。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        stack = []
        maxArea = 0

        for i, h in enumerate(heights):
            start = i
            while stack and stack[-1][1] > h:
                idx, height = stack.pop()
                maxArea = max(maxArea, height * (i - idx))
                start = idx
            
            stack.append((start, h))
        
        for idx, h in stack:
            maxArea = max(maxArea, h * (len(heights) - idx))
        
        return maxArea

注意：程式中的(i - idx)代表著如上圖有些長方形可以往前延伸，所以我們要計算出正確的寬度。另外，經過第一個for迴圈後殘存在stack呈現遞增增長高度的長條一定包含最後一個長條從這個長條所在的index和其他長條的index之間的距離就是各個殘存在stack中的長條的寬度。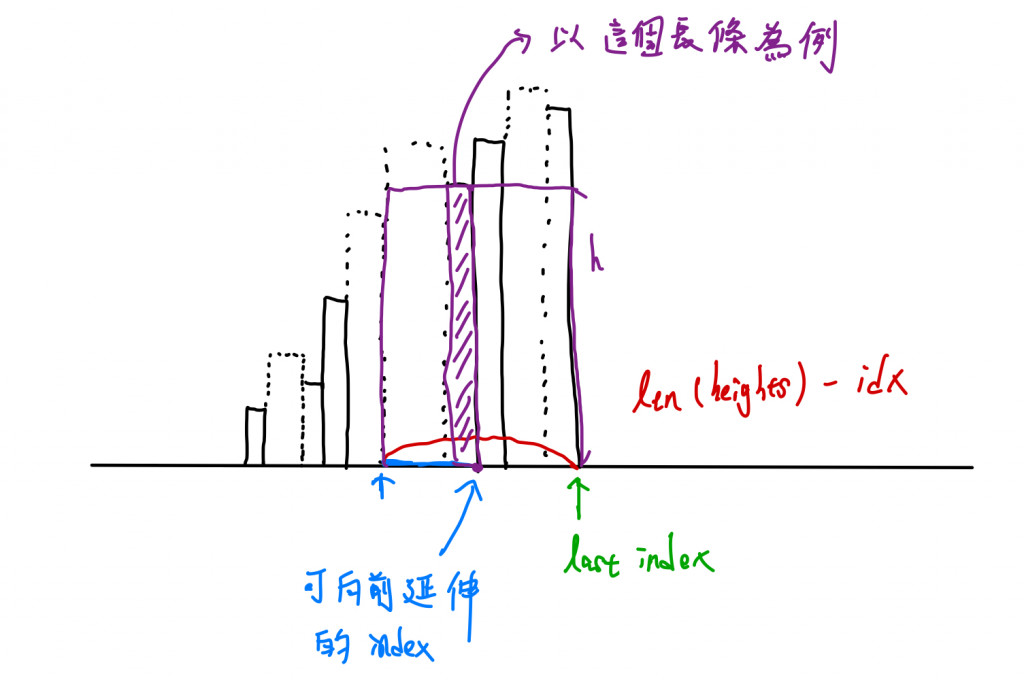

Leetcode 739. Daily Temperatures

題目敘述：input是一個包含了連續好幾天的當天氣溫的array。我們要找出對於第i天，要「過幾天」才能找到比第i天的氣溫更高的日子。如果找不到就以0紀錄。

Example:

Input: temperatures = [73,74,75,71,69,72,76,73]
Output: [1,1,4,2,1,1,0,0]

分析：如上面的範例，如果我們要找到比75還要大的數字，並且間隔了幾天。在這途中還需要紀錄71和69...這些在75後面那幾天的氣溫。所以我們需要一個stack去紀錄第i天的(氣溫, index)並且只要之後的氣溫比紀錄中的高，stack就需要一直pop。（不覺得這和上一題的while迴圈的觀念類似嗎，只是一個要讓stack保持遞增；一個是要遞減）

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        stack = [(temperatures[0], 0)]
        ans = [0] * len(temperatures)

        for i in range(1, len(temperatures)):
            while stack and stack[-1][0] < temperatures[i]:
                _, idx = stack.pop()
                ans[idx] = i -idx
            stack.append((temperatures[i], i))
        
        return ans

Leetcode 155. Min Stack

題目敘述：設計一個stack，擁有一個專門存取整數的stack該具備的函數，push, pop, top。除此之外還要有一個getMin的函數專門回傳目前stack中的最小值。並且這些函數的運算都應該是O(1)。

Example:

Input
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

Output
[null,null,null,null,-3,null,0,-2]

Explanation
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); // return -3
minStack.pop();
minStack.top();    // return 0
minStack.getMin(); // return -2

分析：這是一個跟design相關的有趣的(?)問題。最困難的地方在於題目限制了所有的方法都要在O(1)完成。在我們push一個整數進去stack時，我們可以順便紀錄當下的最小值，我們不會只用一個整數紀錄，而是把當下的最小值也放入到另一個stack中。當要pop時，兩個stack都會pop，來維持stack當下的最小值。

push整數到stack的同時，決定誰是最小值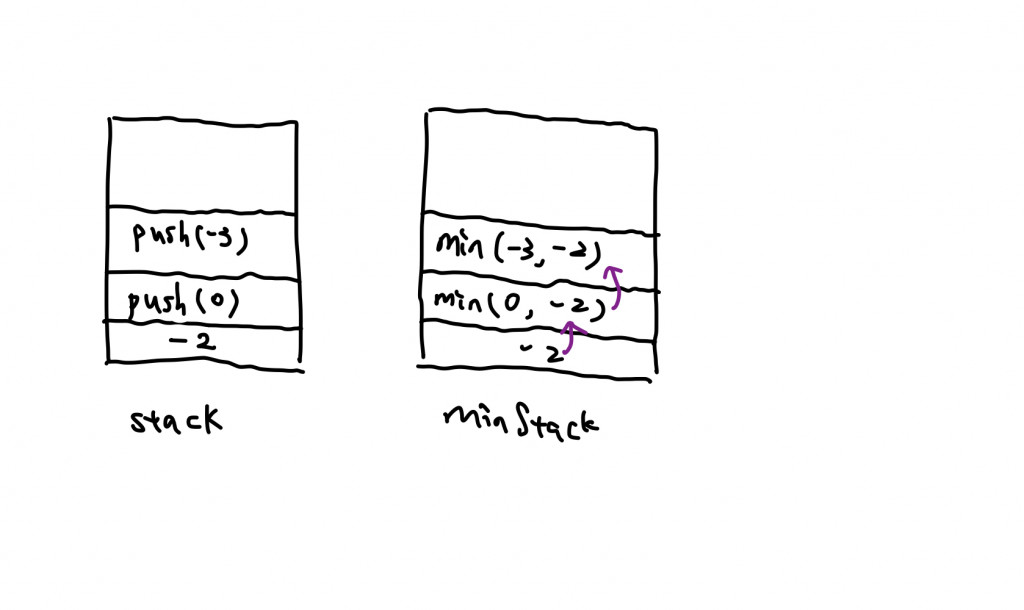

pop掉後，因為我們一直有維護當下的最小值，所以getMin還是能得到正確的答案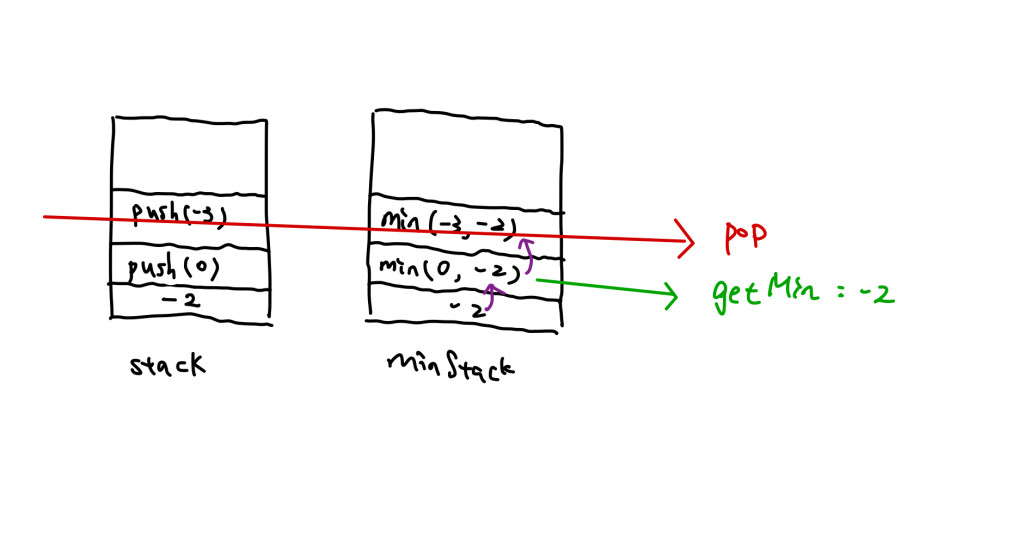

以Python程式碼實作

class MinStack:

    def __init__(self):
        self.stack = []
        self.minStack = []

    def push(self, val: int) -> None:
        self.stack.append(val)
        self.minStack.append(min(val, self.minStack[-1] if self.minStack else val))

    def pop(self) -> None:
        self.stack.pop()
        self.minStack.pop()

    def top(self) -> int:
        return self.stack[-1]

    def getMin(self) -> int:
        return self.minStack[-1]


# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(val)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()

後記：謝謝大家看今天的文章