Hi 大家好，今天要來分享binary search的進階題～

153. Find Minimum in Rotated Sorted Array

題目敘述：有一個整數的array，原本是按照遞增的順序排列，但經過扭轉後會變成有兩段以遞增排列的數列，找出這個array的最小值。並且要求以O(logn)完成。

Example1:

Input: nums = [3,4,5,1,2]
Output: 1

Example2:

Input: nums = [4,5,6,7,0,1,2]
Output: 0

分析：
看到要求要O(logn)就幾乎可以肯定是要用binary search解題。
本題屬於第一型的題目，雖然前面有說第一型的題目比較直觀，但還是有會讓人意想不到的題目。首先我們將問題圖示化：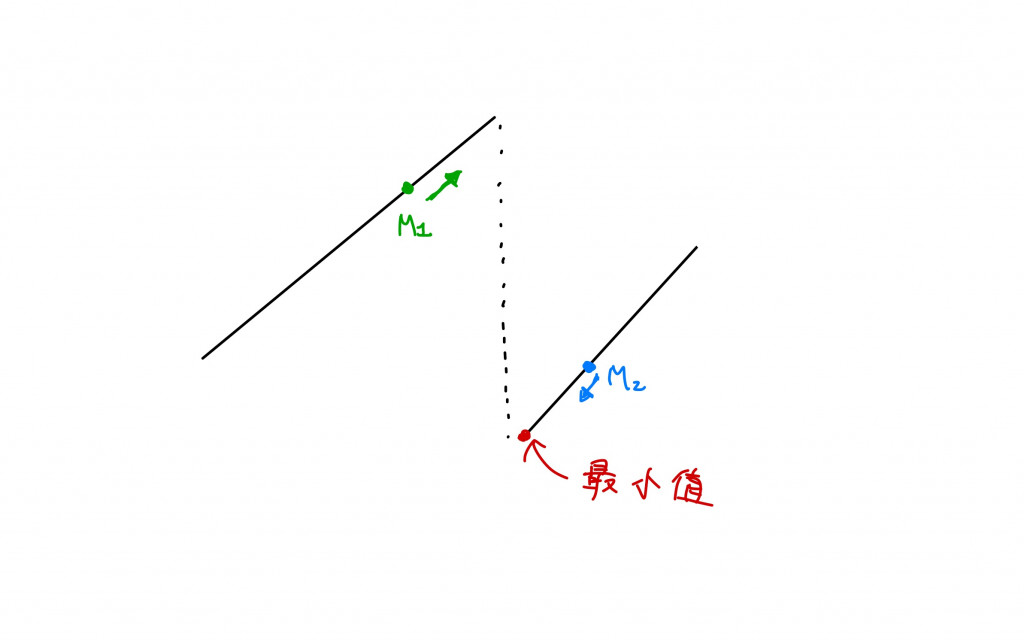

從上圖中可以看出，要找的最小值會在第二段的數列的第一個位置，所以我們要首先判斷目前比較的值會落在第一段的數列還是第二段的數列，第一段的數列的任意值都會比第二段數列的最大值還要大，所以這是我們判斷的依據。如果落在第一段數列代表我們要將左指標向左推，如果現在的中間值比第二段的最大值要小就代表到達了第二段的某一個位置。最後我們要回傳的是左指標，因為他會不斷地向右邊移動直到移動到最小值上。

class Solution:
    def findMin(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = (l + r) // 2
            if nums[m] > nums[-1]:
                l = m + 1
            else:
                r = m - 1
        
        return nums[l]

Follow up: 33. Search in Rotated Sorted Array

如果上面那提做出來的話，這題就會變得很簡單。

題目敘述：有一個被扭轉的整數array，給予一個目標值請用O(logn)的時間複雜度找出array中等於目標值的index，沒有的話回傳-1。

Example:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

分析：

1. 先找出array的最小值的index
2. 判斷目標值位於哪一段數列中
3. 對該數列進行binary search

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums) - 1
        start = -1

        while l <= r:    
            m = (l + r) // 2                       
            if nums[m] > nums[-1]:
                l = m + 1
            else:
                r = m - 1

        start = l
        
        if target > nums[-1]:
            l, r = 0, start - 1
        else:
            l, r = start, len(nums) - 1

        while l <= r:
            m = (l + r) // 2
            if target > nums[m]:
                l = m + 1
            elif target < nums[m]:
                r = m - 1
            else:
                return m
        
        return -1

Leetcode Median of Two Sorted Arrays

題目敘述：有兩個分別排序好的array，找出這兩個array的數值的中位數，時間複雜度為O(log (m+n))。

Example1:

Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.

Example2:

Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

分析：本題也可以利用O(m+n)方式解出來，但是題目有時間複雜度的限制。若要使用binary search來解題的話，本題屬於綜合型，不是個簡單的問題。
首先考慮有一個array，要從中找出中位數，我們首先要考慮這條array的長度，是奇數還是偶數。比如長度為奇數的話，比如長度為9我們要找到第五小的數字：假設我們可以找出前四小的數字，無關這四個數字之間的實際排序，下一個最小值就是第五小的數字。
如今我們的array有兩條，我們可以知道這兩條array的總長度，而中位數會出現排序為「總長度除以2再加1」的位置（如果是奇數長度的話），所以我們要找出前50%小的數字他們在這兩條array的範圍，我們可以針對其中一條比較短的array(A)進行binary search，會得到middle index i，而我們可以將一半的長度扣掉i來得到位在另一個array(B)上的index為j：

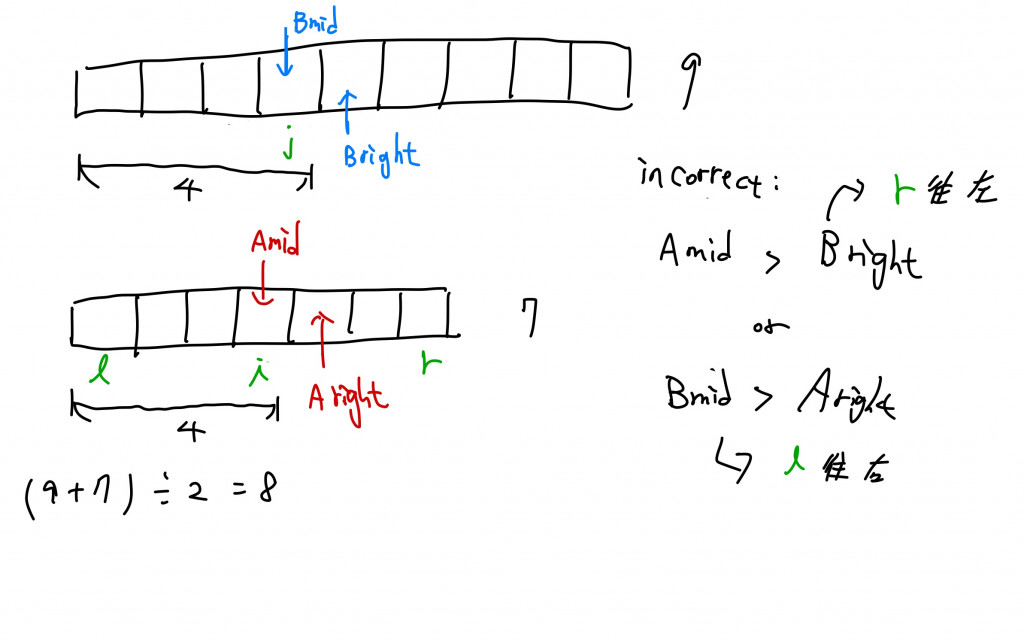
但是我們不能確定剛好前50%的最小值會是這樣平均分佈在兩條array中，所以我們要去確認以下兩種狀況：
如果index i的值Amid > index j的下一個值Bright，代表array(A)收錄了太多的數字，要排除一些；
如果index j的值Bmid > index i的下一個值Aright，代表array(B)收錄了太多的數字，要排除一些。
這兩種狀況我們利用binary search去調整index i。

因為兩個array都已排序，所以Aright或Bright其中較小的值會是「第2/n + 1小的數字」，n代表兩array長度和。

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        half = (len(nums1) + len(nums2)) // 2
        
        if len(nums1) >= len(nums2):
            A, B = nums2, nums1
        else:
            A, B = nums1, nums2
        
        l, r = 0, len(A) - 1
        
        while True:
            i = (l + r) // 2
            j = half - i - 2
            
            Amid = A[i] if i >= 0 else float('-inf')
            Bmid = B[j] if j >= 0 else float('-inf')
            Aright = A[i + 1] if i + 1 < len(A) else float('inf')
            Bright = B[j + 1] if j + 1 < len(B) else float('inf')

            if Amid > Bright:
                r = i - 1
            elif Bmid > Aright:
                l = i + 1
            else:
                if (len(nums1) + len(nums2)) % 2 == 0:
                    return (max(Amid, Bmid) + min(Aright, Bright)) / 2
                else:
                    return min(Aright, Bright)
            

謝謝大家的觀看