大家好，今天要來分享Trie的進階題。

Leetcode 212. Word Search II

題目敘述：
有一個m x n的二維陣列，裡面存放了字元，另外又給予一個裝有數個字串的list，從二維陣列中找出所有包含在list中的字串。

Example1: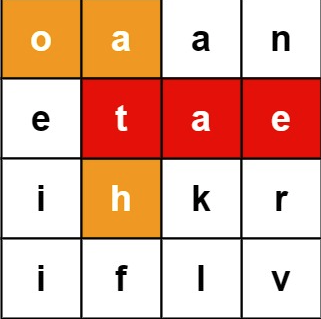

(圖源：leetcode)

Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

分析：
我們可以利用DFS去拜訪二維陣列中的cell，比如說從左上角的"o"開始拜訪，接下來可以拜訪他的下方就讓拜訪的字串變成"oe"或是往右邊拜訪變成"oa"，這樣子得到的字串我們可以拿去和list中的每一個字串（["oath","pea","eat","rain"]）的前幾個字比較，然後發現往下走沒有符合的，所以往右走才有繼續比較的可能性。也就是說這是一個Back tracking的問題，我們需要去紀錄哪種走法所得到的字元排列出來會符合list中的字串。
但是比較字串的方法如果以上述來說可以有更優雅的方法，就是將list中的字串以Trie的方式儲存，因為這些拜訪了字元所組成的字串可以視為某些字串的prefix的可能。同時會紀錄哪些Trie節點被共用了幾次：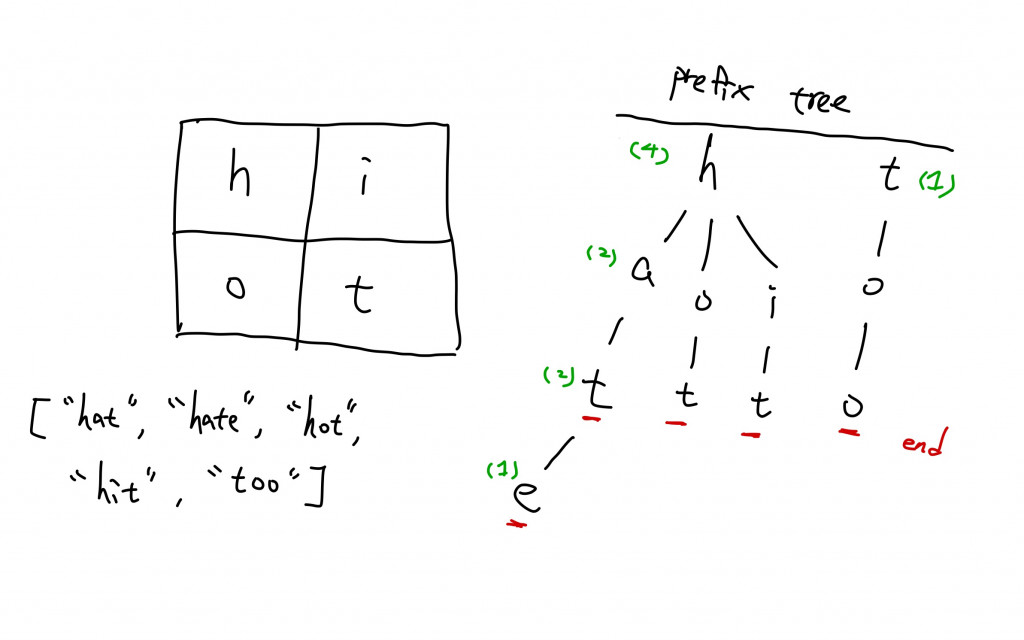

紀錄節點被使用了幾次是因為在Backtracking時，我們如果在二維陣列上找到了某個符合的字串，要將這個字串(path)上的所有node的「使用次數都分別減一」。當某個節點的次數少於1時，代表包含這個節點所組成的字串已經全部找到，不用再找了。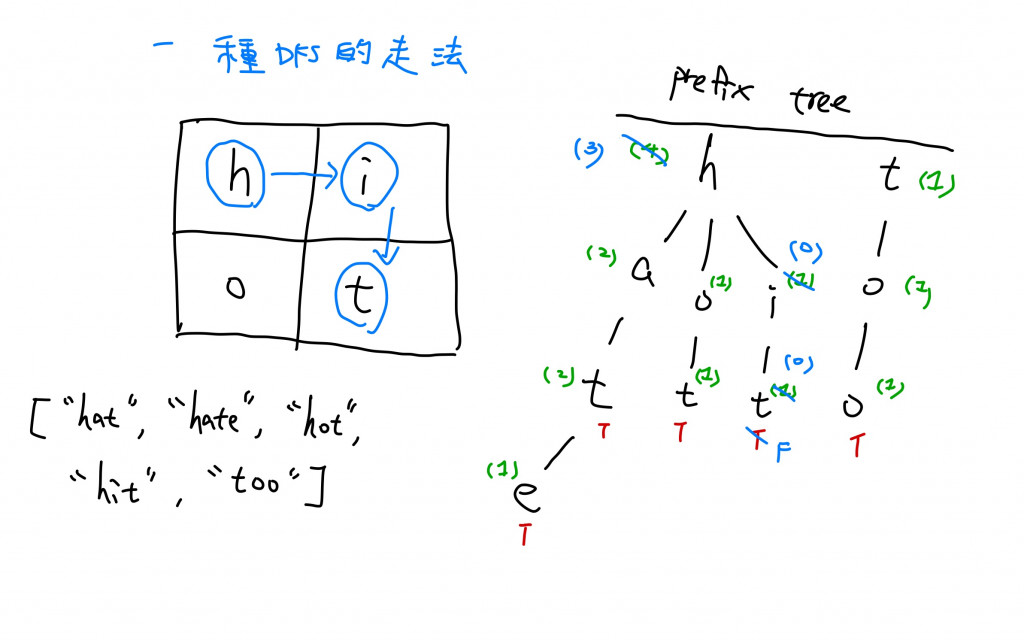

class TrieNode:
    def __init__(self):
        self.children = {}
        self.isWord = False
        self.refs = 0

    def addWord(self, word):
        cur = self
        cur.refs += 1
        for c in word:
            if c not in cur.children:
                cur.children[c] = TrieNode()
            cur = cur.children[c]
            cur.refs += 1
        cur.isWord = True

    def removeWord(self, word):
        cur = self
        cur.refs -= 1
        for c in word:
            if c in cur.children:
                cur = cur.children[c]
                cur.refs -= 1


class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        root = TrieNode()
        for w in words:
            root.addWord(w)
        

        ROWS, COLS = len(board), len(board[0])
        res, visit = set(), set()

        def dfs(r, c, node, word):
            if (
                r < 0
                or c < 0
                or r == ROWS
                or c == COLS
                or board[r][c] not in node.children
                or node.children[board[r][c]].refs < 1
                or (r, c) in visit
            ):
                return

            visit.add((r, c))
            node = node.children[board[r][c]]
            word += board[r][c]
            if node.isWord:
                node.isWord = False
                res.add(word)
                root.removeWord(word)

            dfs(r + 1, c, node, word)
            dfs(r - 1, c, node, word)
            dfs(r, c + 1, node, word)
            dfs(r, c - 1, node, word)
            visit.remove((r, c))

        for r in range(ROWS):
            for c in range(COLS):
                dfs(r, c, root, "")

        return list(res)

我們在dfs這個用來進行back tracking的函數中判斷是否要繼續拜訪board中的某個cell時，也會去判斷剛才提到某個字元是否在Trie Node中並且他不是沒有用的節點(refs < 1)。當我們發現已經找到符合Trie中的某個字串時（node.isWord == True)時，就會將這個字串的終點設定為False，並且這個在Trie中組合出這個字串的節點都減少一次使用的次數(removeWord)。

Trie是個很適合用來搜尋字串的資料結構，但是如果有其他比較簡單的方法(hashmap, linked list...)可以達成題目的需求，就未必一開始就使用這個資料結構。