連假結束了，好不想面對現實

二元樹的特例

自平衡樹是一種特殊的二元搜尋樹（Binary Search Tree，BST），它具有自動調整樹結構的能力，以確保樹保持平衡。在深入討論自平衡樹之前，讓我們先回顧一下二元樹的特例:

1. 歪斜樹（Skewed Binary Tree）： 歪斜樹是一種極端不平衡的樹，其中所有節點都只有一個子節點，使得樹呈現線性結構。這會導致查找操作的時間複雜度變為O(n)，其中n是節點數量。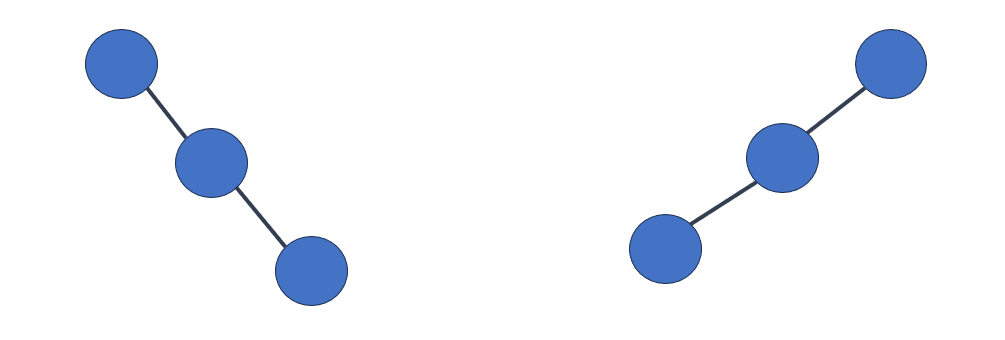
   

2. 完滿二元樹（Fully Binary Tree）： 完滿二元樹是一種每個節點都有兩個子節點的樹，所有葉子節點都在相同的層級上。這種樹具有最佳的平衡性，但在實際應用中較少見。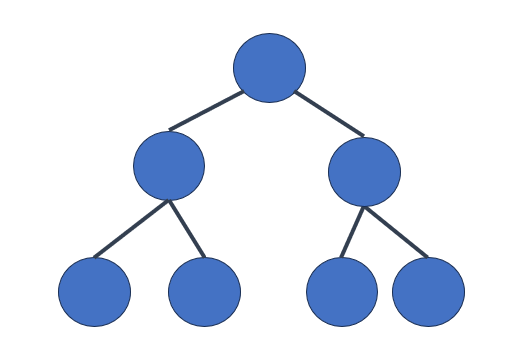
   

3. 完整二元樹（Complete Binary Tree）： 完整二元樹是一種樹，其中每個節點都有兩個子節點，但在最底層的葉子節點可能有缺失。這種樹保持了平衡性，並在某些情況下具有實際應用價值。

為什麼需要自平衡

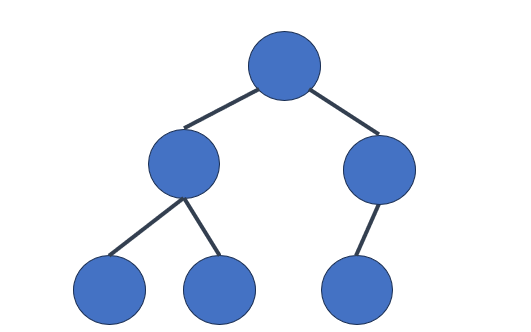
現在，讓我們談談不平衡樹以及為什麼需要自平衡樹：

不平衡樹指的是在二元搜尋樹（Binary Search Tree，BST）中，樹的結構讓其中一個子樹比另一個子樹更深或更高，導致樹的高度失衡。這樣的不平衡情況可能會導致基本操作（如查找、插入、刪除）的時間複雜度變差，因為它們的性能取決於樹的高度。

具體來說，當BST變得極度不平衡時，可能會導致以下問題：

• 查找效率降低： 當BST變得極度不平衡時，樹的高度接近線性，導致查找操作的時間複雜度達到O(n)，而不是理想的O(log n)。

• 插入和刪除操作變慢： 插入和刪除操作的效率也受到不平衡樹的影響，因為它們需要維持樹的有序性，這可能需要大量的旋轉和重新結構操作，導致性能下降。

• 資料存儲不均勻： 不平衡樹可能導致節點的深度不均勻，使得某些操作的性能波動很大。

為了解決這些問題，我們引入了自平衡樹，它們可以在插入和刪除操作時自動調整樹的結構，以確保樹保持平衡。

常見的自平衡樹

以下是一些常見的自平衡樹類型：

1. AVL樹(AVL Tree)： AVL樹使用平衡因子（Balance Factor）來確保樹的平衡，通過旋轉操作來調整。平衡因子是左子樹的高度減去右子樹的高度，必須保持在一個特定的範圍內。
2. AA樹(AA Tree)： AA樹是一種自平衡樹，通過特定的旋轉和重構操作來保持平衡。它具有較簡單的平衡規則，並在實現上比AVL樹更簡單。
3. 紅黑樹(Red-Black Tree)： 紅黑樹是最常見的自平衡樹之一，通過設置節點的顏色（紅色或黑色）以及遵守一組紅黑規則，確保樹的平衡。這種結構確保了樹的高度保持在O(log n)範圍內。
4. 伸展樹 (Splay Tree)： 通過伸展操作將訪問的節點移到樹的根位置，以提高未來對該節點的訪問效率。
5. B-樹(B-Tree)： B-樹是多向樹，通常用於磁碟存儲和數據庫系統中，以確保高效的插入和查找操作。
6. 替罪羊樹(Scapegoat Tree)： 替罪羊樹部分自平衡，當達到一定深度時，會重建子樹以保持平衡。這種方法在某些情況下可以有效地維護平衡。
7. 樹堆(Treap)： Treap是一種隨機化的自平衡樹，使用優先級值進行節點排序。它結合了二叉搜索樹的特性和隨機性，以確保平衡。
8. 權重平衡樹(Weight Balanced Trees)： 其中每個節點的左子樹中的節點數至少是右子樹中節點數的一半，最多是右子樹中節點數的兩倍。它是一棵基於搜尋每個單獨節點的機率的知識平衡的二元樹。

每種自平衡樹都有其獨特的優勢和適用場景，選擇適合特定需求的自平衡樹取決於應用程序的性能要求和操作模式。

今天就先分享到這，剩下的明天繼續。

逃避只會延遲我們的進步，而真正的成就來自於克服挑戰和堅持不懈。