Connected Component(連通元件)是圖論和電腦科學領域常用的概念。它通常用於描述圖形或網路中的一組相關節點(或頂點),這些節點透過邊(或連結)相互連接。一個連通元件是一個子圖,其中每對節點之間都存在一條路徑,這意味著你可以從該連通元件中的任何一個節點到達其中的任何其他節點。
1.連通圖(Connected Graph):一個連通圖是一個圖,其中每一對節點都有至少一條路徑相連。也就是說,從圖中的任何一個節點出發,可以到達圖中的任何其他節點。
2.連通分量(Connected Component):一個連通分量是一個連通圖中的極大連通子圖,這意味著無法將其擴展為更大的連通子圖,而且該連通分量中的任意節點都不能透過邊連接到其他連通分量中的節點。連通分量可以是單一節點(孤立點)或包含多個節點。
3.強連通分量(Strongly Connected Component):強連通分量是在有向圖中定義的概念,其中對於每對節點u和v,存在從u到v和從v到u的有向路徑。換句話說,任兩個節點之間都可以互相達到。
與連通元件相關的演算法主要用於圖論和網路分析,以確定和處理圖中的連結性和關係。以下是一些與連通元件相關的常見演算法:
1.Tarjan's Algorithm:用於尋找有向圖中的強連通分量。它基於深度優先搜索,並透過堆疊來追蹤分量的發現,用於識別強連通子圖。
2.Kosaraju's Algorithm:用於尋找有向圖中的強連通分量,它透過兩次深度優先搜尋來實現,首次搜尋找到反向圖的拓撲排序,然後在原始圖上進行搜尋以確定強連通分量。
Tarjan's Algorithm 是用來找出有向圖中強連通分量的經典演算法,由美國電腦科學家 Robert Tarjan 在1972年提出。強連通分量是一個圖中的節點子集,其中每對節點之間都存在著互相可達的路徑。這個演算法透過深度優先搜尋(DFS)來實現。以下是 Tarjan's Algorithm 的步驟和方法介紹:
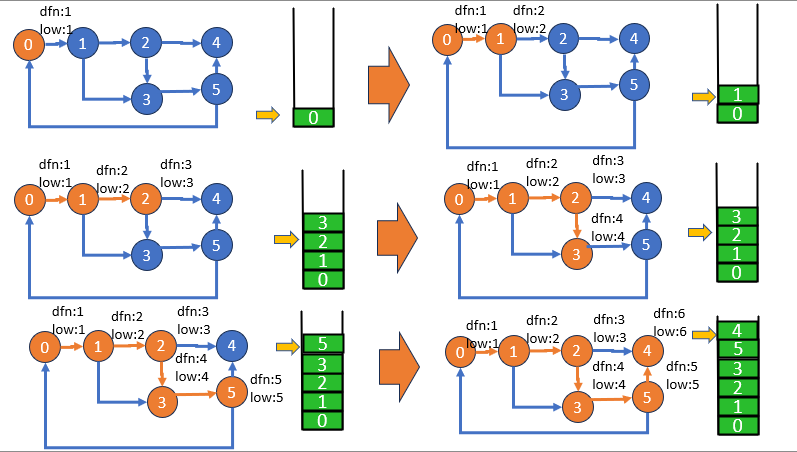
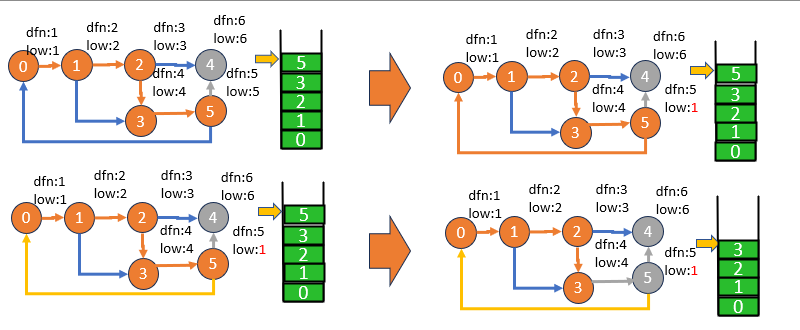
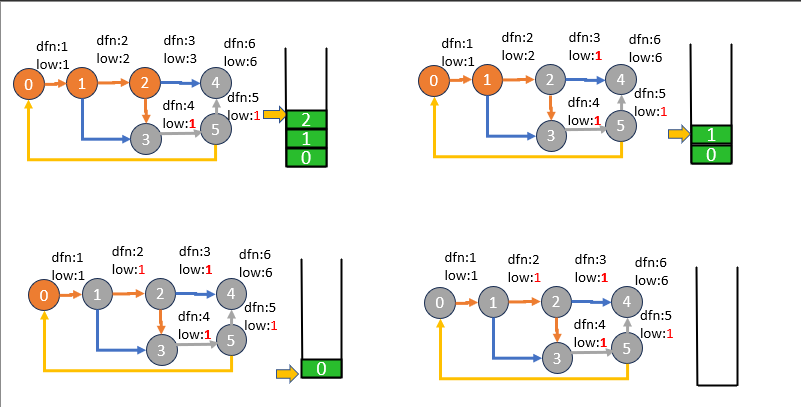
void tarjan(int u){
// 從u點開始進行tarjan算法
dfn[u] = low[u] = ++cnt; // 設置訪問順序
tarjanStack.push(u); // 將該點壓入stack
inStack[u] = true; // 該點在stack中
// 遍歷u點的所有鄰接點
for(int i = 0 ; i < adj[u].size() ; i++){
int v = adj[u][i];
if(!dfn[v]){ // 如果該點沒有被訪問過
tarjan(v); // 遞歸訪問
low[u] = min(low[u], low[v]); // 更新能到達的最早的點
}else if(inStack[v]){ // 如果該點在stack中
low[u] = min(low[u], dfn[v]); // 更新能到達的最早的點
}
}
// 如果該點能到達的最早的點等於自己, 則該點為強連通分量的根
if(dfn[u] == low[u]){
vector<int> strongComponent; // 創建一個強連通分量
int v;
do{
v = tarjanStack.top(); // 從stack中取出一個點
tarjanStack.pop();
inStack[v] = false; // 該點不在stack中
strongComponent.push_back(v); // 將該點加入強連通分量
}while(u != v); // 直到該點等於u
strongComponents.push_back(strongComponent); // 將強連通分量加入強連通分量集合
sccCnt++; // 強連通分量個數加一
}
}
Kosaraju's Algorithm(科薩拉朱演算法)是一種用於尋找有向圖中強連通分量(Strongly Connected Components,SCC)的演算法。這個演算法由美國電腦科學家 Sharad S. S. Kosaraju 在1978年提出,它透過兩次深度優先搜尋(DFS)來找到有向圖中的強連通分量。 SCC是指在有向圖中,每個節點都可以透過有向路徑到達其他每個節點的一組節點。
以下是Kosaraju's Algorithm的詳細步驟:
1.將所有頂點初始化為未訪問過
2.每個未造訪的節點開始,執行深度優先搜尋(DFS)
3.建構反向圖:把原始圖的邊的方向反轉
4.將反轉圖中的所有頂點標記為未訪問
4.從同一頂點 v 開始對反轉圖進行 DFS 遍歷
class Kosaraju {
private:
int vertices;
std::vector<std::vector<int>> adjList;
std::vector<bool> visited;
std::stack<int> order;
void DFS1(int v) { //DFS1: 用來找出訪問順序
visited[v] = true;
for (int neighbor : adjList[v]) {
if (!visited[neighbor]) {
DFS1(neighbor);
}
}
order.push(v);
}
void DFS2(int v) { //DFS2: 用來找出強連通分量
visited[v] = true;
std::cout << v << " "; // 印出該點
for (int neighbor : adjList[v]) {
if (!visited[neighbor]) {
DFS2(neighbor);
}
}
}
public:
Kosaraju(int v) : vertices(v) { // 初始化
adjList.resize(vertices);
visited.assign(vertices, false);
}
void addEdge(int from, int to) { // 加邊
adjList[from].push_back(to);
}
void findSCCs() { // 找出強連通分量
for (int i = 0; i < vertices; i++) { // 先找出訪問順序
if (!visited[i]) {
DFS1(i);
}
}
// 反轉圖
std::vector<std::vector<int>> reversedAdjList(vertices);
// reversedAdjList: 反轉圖的鄰接表
for (int i = 0; i < vertices; i++) {
for (int neighbor : adjList[i]) {
reversedAdjList[neighbor].push_back(i);
}
}
visited.assign(vertices, false);
// 依照訪問順序找出強連通分量
while (!order.empty()) {
int v = order.top();
order.pop();
if (!visited[v]) {
std::cout << "SCC: ";
DFS2(v);
std::cout << std::endl;
}
}
}
};
| 特點 | Kosaraju's Algorithm | Tarjan's Algorithm |
|---|---|---|
| 作者 | Sharad S. Sarnak and Satish Rao | Robert Tarjan |
| 目的 | 找到有向圖的強連通分量 | 找到有向圖的強連通分量 |
| 遞迴/迭代 | 遞迴 | 遞迴或迭代 |
| 難易度 | 相對複雜 | 相對簡單 |
| 效率 | O(V + E) | O(V + E) |
| 適用範圍 | 小型圖或稀疏圖 | 大型圖或稠密圖 |
| 佔用內存 佔用內存相對較多 | 佔用內存相對較少 | |
| 計算強連通分量的數目 | 需要額外計數步驟 | 在算法過程中即可計數 |
這兩個算法都用於找到有向圖中的強連通分量,但它們有不同的實現方式和性能特點。Kosaraju算法相對複雜,但對於小型或稀疏圖可能更合適,而Tarjan算法相對簡單且內存效率較高,適用於大型或稠密圖。選擇哪個算法取決於您的具體需求和圖的性質。
不怕找不到人生意義,因為你的存在本身就是有意義的。
