這兩題的解法就跟上一篇講的一樣，基本上就是要想辦法用雙指針演算法去解題。

141. Linked List Cycle

題目

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

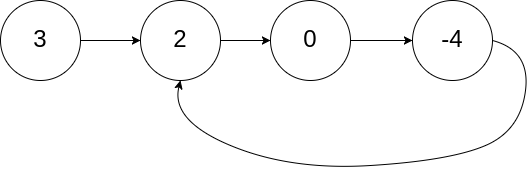
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

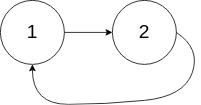
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 10^4].
• 10^5 <= Node.val <= 10^5
• pos is 1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

解法(Java)

Runtime: 0 ms
Memory Usage: 43.2 MB

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) return false;
        
        ListNode slow = head;
        ListNode fast = head;
        
        while (fast != null && fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) return true;
        }
        return false;
    }
}

142. Linked List Cycle II

題目

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

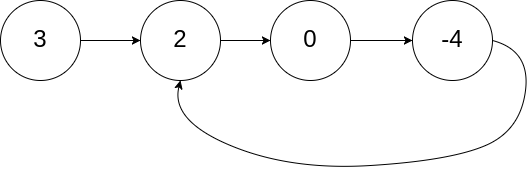
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

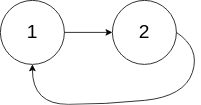
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].
• 105 <= Node.val <= 105
• pos is 1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

解法(Java)

這題寫了兩個解法，第一個一樣是用雙指針演算法去解，先使用slow和fast判斷是否有循環結構，如果有循環結構的話就從slow和fast相遇的節點，開始讓head和fast同步往前至循環結構的交會點。

Runtime: 0 ms
Memory Usage: 43.3 MB

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null) return null;

        ListNode slow = head;
        ListNode fast = head;

        while (fast.next != null && fast.next.next !=null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                while (head != fast) {
                    head = head.next;
                    fast = fast.next;
                }
                return head;
            }
        }

        return null;
    }
}

第二個解法則是我試了一下，使用Set去儲存看過的節點，如果在遇到尾端(null)前碰到看過的節點，那個節點就是循環結構的交會點。

Runtime: 2 ms
Memory Usage: 43.6 MB

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null) return null;
        Set<ListNode> seen = new HashSet<>();

        ListNode temp = head;
        while (seen.add(temp)) {
            if (temp.next != null) {
                temp = temp.next;
            } else {
                return null;
            }
        }

        return temp;
    }
}

小結

這兩題就是上一篇文章帶出的題目，練習使用雙指針演算法去解題，在第二題有嘗試使用其他解法，但不管是時間還是空間上都輸雙指針演算法。