前言

昨天介紹了DDPM，希望各位沒有被複雜的數學原理轟炸到，如果有的話，很抱歉今天會再被轟炸一次，不過基本原理昨天以及帶各位算完了，今天的數學量會比昨天少很多。

那今天要來介紹Denoising Diffusion Implicit Models (DDIM)，接著就來看看這個模型與DDPM的不同吧，以及它如何改良了DDPM運算、採樣速度慢的問題。

如果還未了解DDPM原理的人，可以看看我昨天分享的文章。

DDIM是甚麼？

DDIM是DDPM的一種變種，他改良了DDPM在使用馬可夫鏈採樣時需要花費大量時間的問題。雖然DDIM在採樣時使用的方式與DDPM幾乎是不同的，但是據論文作者所述他們的方法與DDPM的訓練目標一致，所以可以當成單純改良了DDPM的缺點，使其逆向擴散可以更快地採樣，接下來就來看看這個模型的細節吧。

今天的圖片基本上都源自於DDPM原始論文和DDIM原始論文，若有其他來源會另外標註。

DDIM與DDPM的不同

首先來概述一下DDIM與DDPM的不同，DDIM全名為Denoising Diffusion Implicit Models，名字中的Implicit代表的隱式，這個字就是DDIM與DDPM的第一個不同：

1. 這個字的意思代表DDIM使用了一種隱式的分布來近似真實分布；而DDPM是使用顯式的分布來近似真實分布 (昨天說到的讓前向擴散與逆向擴散的常態分佈變成越接近越好的的)。
2. DDIM使用了動態的方式來採樣；而DDPM是遵照著馬可夫鏈，使用固定的變異數來採樣。
3. DDIM可以跳過一些擴散時間進行採樣；但DDPM必須遵照時間一個一個採樣。這代表DDIM可以預測可能10個擴散時間後的結果，這就代表比起一次1個擴散時間的DDPM，DDIM的速度就被增加了10倍！

DDIM如何做到加速？

昨天介紹的DDPM，回顧一下期前向與逆向擴散的過程，我們可以根據可以慢慢推導出來，接著DDIM的作者就想說如果把每個時間步t變成2t、3t…呢？那不就一次跳好幾步了嗎？

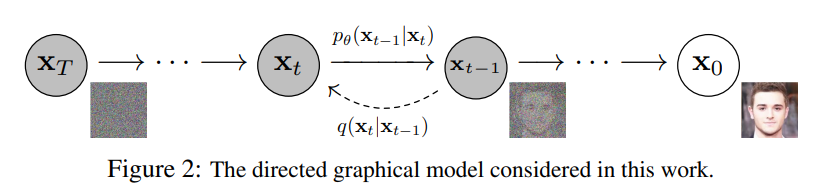
圖. DDPM的前向與逆向擴散概念

可以看到DDIM想要跳脫馬可夫鏈只能一步一步擴散的侷限，他將擴散方式變成，如下圖。為了更好的了解公式，所以的、會改寫成、，以更方便了解擴散時間之間的關係：

圖. DDIM的思路

這個部分我們要來要根據貝氏定理來出發，逐步探討DDIM是怎麼做到加速的：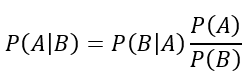

將貝氏定理帶入的話就會變成下面的方程式，這個方程式記為方程式1.：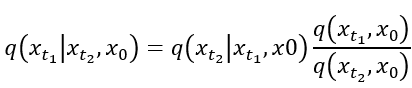

是我們要求的，也就是前向擴散的部分。如果我們假設t2是t1過5步以後的結果，那就代表採樣速度快了5倍。接著要求的就是如何計算，我們根據昨天 介紹到的公式：

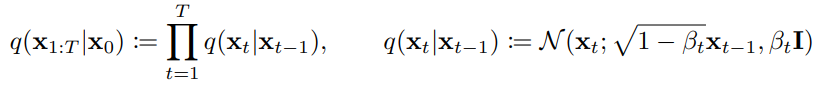
主要是要把改成由t與t-1來決定的變量，這也對應到了與DDPM的第2個不同點，DDIM擴散時的變異數是不固定的，他由時間步來決定。我們來看看DDIM論文中的公式：

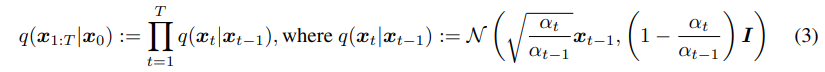
我們發現作者他把DDPM中公式的改寫成的形式，其中關係式是這樣的：

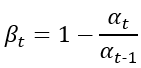
將這個公式帶入到的公式並把變成；變成，就可以得知上述貝式定理(方程式1.)等號右邊的所有部分，接著就能計算出結果，而此結果就是我們要的逆向擴散部分。

綜上所述，這就是DDIM所做的變動，他把馬可夫鏈改掉，變成另外一種可以透過貝氏定理加速採樣的過程 (就是與DDPM的第3個不同點)，其他的公式，目標函數基本上並無變化。所以訓練目標還是相同的。

再來看看逆擴散的眉角，隱式模型怎麼來的

昨天有介紹到DDPM的前向擴散的分布公式：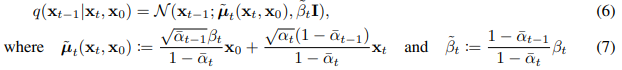

我們發現有一個東東，是頭上長了毛毛蟲的符號，昨天有說到它是前向擴散期望分布的變異數，這個方程式作為方程式2.，等等還會用到：

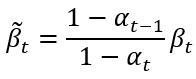
我們將帶入到原公式並全面取代之後會變成這樣：

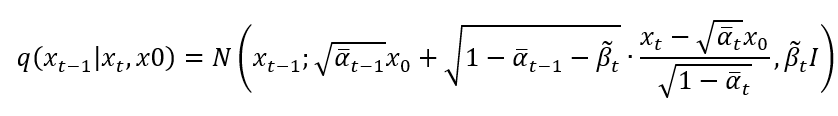
假設今天將變異數設定成0，也就是上面有毛毛蟲的時，這代表逆擴散過程變成沒有雜訊干擾的過程，也代表不像普通的DDPM在逆向擴散的時候會從常態分佈採樣。從常態分佈採樣會使得過程具有隨機性，將這個隨機性去除掉了以後，今天我們輸入了一張雜訊，就只會得到唯一的採樣結果，使逆向擴散不再具備隨機性。這種結果已經確定、沒有隨機因素的機率模型被稱作隱式機率模型 (Implicit Probabilistic Model)，這就與DDIM的名稱是相同來源。因為作者除了加速採樣過程以外，還將變異數設定為0，所以DDIM的名稱由來是源於此。這個改動對應到了與DDPM的第1個不同點。

變異數造成的影響

上面說到變異數改成0時模型就為DDIM，此時生成結果固定。那如果想玩玩其他變異數呢？別急，作者已經玩過了，在第5章時的Table 1就有統整不同變異數實驗的結果，在這之前我們要先了解作者為了讓變異數可調，新增了一個參數，並且把 方程式2. 加入這個參數，讓他跟原式相乘，變成：

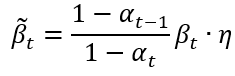
接著就來看看不同的情況、以及不同的擴散時間下生成的圖片其FID指標為何。結果如圖所示：

FID指標是評估生成模型生成圖片品質的指標，基本上數值越小代表生成效果越好。FID指標會在之後討論。

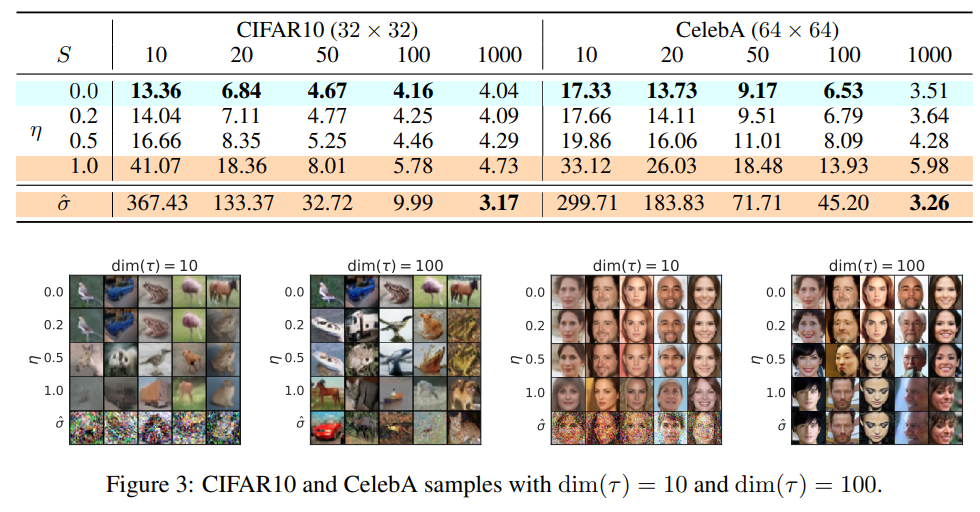
作者使用了CIFAR10與CelebA資料集。前者是用於圖片分類的資料集，共有10個類別的圖像；後者是人臉圖片的資料集。值得一提的是代表標準差設定在一個奇怪的狀態下：

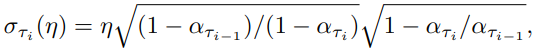
此標準差不能帶入上面的公式，需要使用DDPM模型，方程式的意思是可以當成使用DDPM的變異數：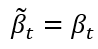

在這個情況下訓練的成果可以解讀成：

1. 在使用加速採樣的情況下當擴散時間少，時效果最好，而的結果差到不行。也就是DDIM效果優於DDPM。
2. 但當擴散時間變長，且逐漸靠近1時模型逐漸類似DDPM，此時使用的效果就會越好。

結論就是當擴散時間很長、採樣時間久的話，DDPM效果自然是最好的 (比DDIM好)；而要降低擴散時間節省時間成本使用DDIM成果會比較好。

結語

今天又是被數學轟炸了一天，不過明天就要來實際實現DDIM了，DDIM的程式我是參考Keras的範例去建立的，不過基本上與原始程式並無太大差別。不過我會盡力解釋裡面的程式碼其意思是甚麼，以讓各位可以更了解DDIM的實現過程。