前言

前幾天介紹了許多生成對抗網路 (GAN)的理論與實作，希望各位都有從中學習到許多。不過這次系列文章也即將進入尾聲，故在最後我想介紹擴散模型。擴散模型始祖是Denoising Diffusion Probabilistic Models (DDPM)，但因為採樣方式實在過於緩慢，所以我將會再介紹改良過後的Denoising Diffusion Implicit Models (DDIM)。雖然數學原理複雜，不過我會分兩天慢慢介紹DDPM與DDIM，希望各位可以盡力理解這兩個模型的細節。

DDPM是我讀的最透徹的論文之一了，之前學習過程中算過了幾乎所有的方程式，知道該模型的複雜點等等。不過作為當今最有潛力的生成模型之一，我覺得要好好介紹最原始的DDPM，讓各位都能了解這個模型的原理。

DDPM是甚麼？

DDPM中文名稱為去噪擴散機率模型，也稱為擴散模型。根據原始論文，研究團隊使用這個模型提供高質量的圖片生成應用，DDPM是一個受非平衡熱力學啟發的潛在變量模型。研究團隊的開源程式碼在這，各位可以去看看。

今天的圖片基本上都源自於原始論文，方程式大部分都是我自己再根據計算以及文獻而自己打Latex出來的，若有錯誤麻煩請在留言區跟我說！圖片的話如果有其他來源會另外標註。

DDPM架構

DDPM訓練基本上是使用參數化的馬可夫鏈 (Markov chain)，透過變分推理的方式訓練，馬可夫鏈的定義是某個大於等於1的時刻t，其隨機變量 只會與前一個時刻 之間有條件分布的關係，並不會依賴更久之前的隨機變量。

馬可夫鏈示意圖，圖源我自己。

DDPM主要內容分成兩個部分：

1. 前向擴散：前向擴散的馬可夫鏈通常會設定一段時間步長。擴散的意思是將圖片轉為雜訊的過程，前向擴散會透過馬克夫鏈為圖片加上雜訊，到達自己設定的指定時間步長T時圖片就會是一個加了很多次雜訊，也就被變成雜訊圖了。前向擴散計算方式如下圖 Figure 2. 的 。

   下方公式是擴散方式的原理，可以看到要得到一個指定時間步需要透過許多加噪音的步驟 (連乘符號 )，以及擴散加雜訊的部分 是從常態分布N中採樣的。其中β是添加雜訊的變異數序列。

   此常態分佈的平均值為下式，這部分可以看成當前這步的狀態 加上了上一步狀態乘上下式，並加上平均為0的常態分布 ；變異數為 。

   

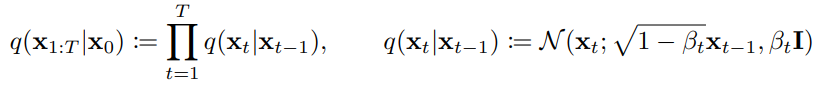
   這部分就是根據 貝氏網路 的基礎而寫出的聯合分布，貝氏網路簡單概括就是利用有向無環圖建立的屬性，以及其之間的依賴關係，並使用條件機率來表示各屬性的聯合機率分布。這種方式可以很好的知道在特定時刻下的情況，所以實作上並不需要真的一步一步加上雜訊。就可以採樣到該時刻的加噪圖片。

2. 逆向擴散：逆向擴散的訓練如下圖，此時這個逆向的擴散過程會搭配神經網路訓練，透過輸入擴散時間與雜訊圖，要盡可能地去學習擴散過程中的雜訊分布！接著再一步一步去噪，並非直接生成原圖！

   是從常態分布N中採樣的。

   此常態分佈的平均值為 ；變異數為

   

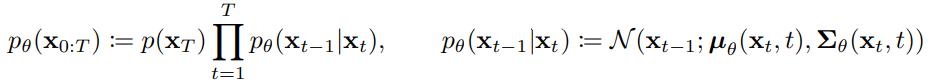
   這個部分與前向擴散不同，去噪過程不能說不容易，只能說幾乎無法直接寫成公式計算 (容易的話就不需要神經網路了)，所以在這階段會使用神經網路來學習去噪過程。

   

重(討)要(厭)的數學推導

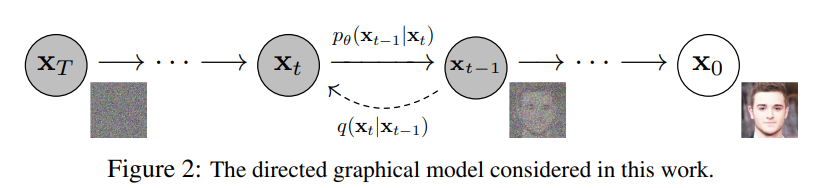
接下來就是複雜的數學推導啦，擴散模型真的比起GAN，原理非常複雜，但這些數學原理又很重要，這邊會一步一步帶各位更深刻的了解逆向擴散的部分！

前向擴散

首先要了解DDPM我們要先從前向擴散下手，剛剛有提到前向擴散的公式：

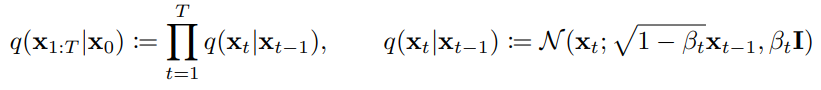
論文中作者假設了一個 ，這個 很重要，它可以將上式改寫成 。有了這個關係後我們可以計算 跟 ：

接著把 帶入計算 的方程中，我們可以算出：

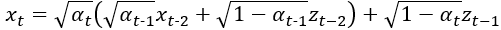
再把 乘進去之後化簡一下，這邊要注意的是兩個常態分佈的雜訊z相加的方式，我們可以將兩個雜訊z的標準差 和 變成變異數，也就是將他們平方後直接相加，做為新的常態分佈雜訊z的變異數，可以發現 被消掉了，接著 跟 可以直接合併，因為他們都是從常態分佈採樣出來的，本質上其實沒差，接著再變回用標準差表示的形式。整個式子會變成：

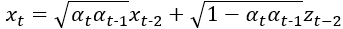
我們可以看出來他就是馬可夫鏈的方式， 又會跟 相關，一直循環到直到 為止，接著根號內部也很神奇，就是 這樣乘直到 ，此時我們可以用連乘符號來表示 ，作者使用了下式來表達。

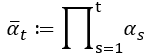
所以將上面兩個東西合併後，整個式子就變成下式，也可以跟論文的方程式 (4)對應上，這樣我們就得到了雜訊 與原圖 的關係式了，這個式子也很重要喔，要記住一下。

要記住變異數是標準差的平方，所以論文中的變異數沒有加開根號。

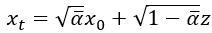
算這個有甚麼用呢，我們將式子移項一下，變成 與 的關係式：

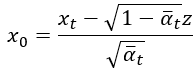
這個先放著，因為等等會計算前向擴散中機率分布的期望估計平均值，在這邊先埋個伏筆。

DDPM目標函數前奏

接著來看看目標函數，文章中使用下列方程式，公式出自於文章中方程式(3)。

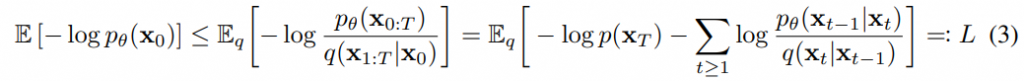
這個東西大家可能有疑問說是如何蹦出這個東東的，其實在另一個生成模型變分自編碼器 (Variational Auto-Encoder, VAE)中會使用VLB (Variational Lower Bound)來優化一個負對數似然 (Negative Log Likelihood, NLL)，這個概念對於VAE的目標函數計算非常非常重要。VLB是變分下界的縮寫，也稱ELBO。詳細的過程在這個參考資料，不過使用ELBO優化NLL的推導並非今天的重點，使用這個方式後根據該篇參考資料的計算結果，我們會得到這個方程：

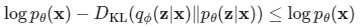
上述方程出自於剛剛提到的 參考資料，接著我們整理一下，移項後並根據DDPM的相關條件改寫後可寫成：

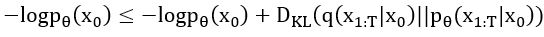
上述方程中KL散度就是要計算前向擴散的方式 ，並訓練神經網路去近似該擴散的方式 ，這兩個分布的相似程度。神經網路學會後就可以生成這個常態分布的雜訊去做逆向擴散，將雜訊還原成原始圖片。

接著要把KL散度打開，KL散度的基本公式在第14天 有介紹到，然後要再寫成期望之形式。再來把 使用條件機率的公式變成 並帶入，具體作法如下，首先將KL散度打開。

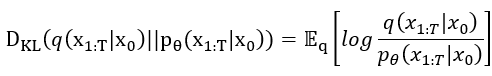
接著把剛剛的條件機率帶進去後，再使用對數率把獨立出來，之後整個方程會變成：

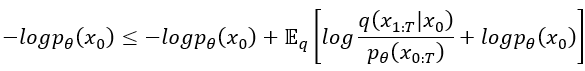
小於等於符號右邊，期望值裡面的 可以拿出來與 抵銷掉，此時方程小於等於符號右邊就簡化成 ，這個需記起來，等等還要用。最後使用對數律，log外面乘以 (-1) 而log裡面取 (-1) 次方，這是對數率的指係(次方公式)，然後就變成了文章中的方程式 (3)了，很神奇吧！

求目標函數

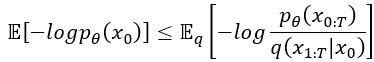
好了，剛剛經過前奏以後，接著要來從剛剛算出來的東西來繼續探討DDPM的目標函數了，大家打起精神來吧~接下來會有點複雜，請各位撐住！

剛剛我們算出了 ，現在要來對它開刀了。首先我們要把它展開：

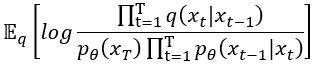
然後我們根據對數律要做兩個動作，

1. 第一個就是把分母的 移到log外面讓它自己獨處。
2. 接著還是對數律，對數函數中的真數如果相乘的話，可以看成許多對數函數相加(和差公式)，所以那個連乘記號 可以直接變成連加記號 ，水喔。

經過上面兩個動作，公式變成：

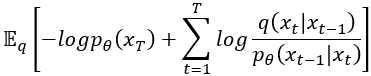
接著把擴散時間 的部份另外拉出來：

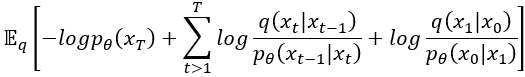
然後把 這方程式的分子部分，根據貝氏定理又加上了條件 ，可以改寫成下式。

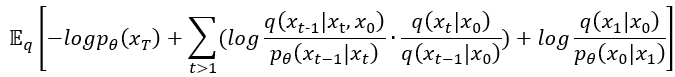
接著整理一下把剛剛新得到的東西也一起獨立出來，也只是老樣子把log裡面的乘法拿到外面變成加法。

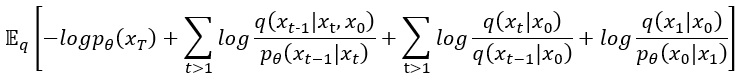
接下來準備收尾了，算這個東西的目的是把它變成許多KL散度組合的方程式，用於理解它且更直觀。先處理掉 使之變成 ，然後就會發現原式除了第二項 以外全部都變成log然後裡面的真數是一個分數，接下來相信不用多說也知道要幹嘛了吧~當然就是把log裡面的除法拿到log外面變減法(和差公式)，運氣好還能消掉一些東西XD。

我們把它展開：

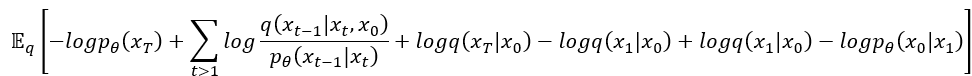
唉呦，看起來可以來消東西了，把 跟 消掉，舒服。

然後我們再整理一下，把 移動到最前面與 送作堆。接著這兩項減法再放到log裡面變成除法，不知不覺就…

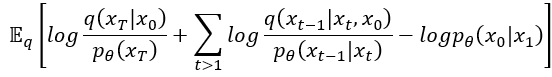
有沒有發現，是不是前兩項都可以寫成KL散度的形式呢？既然可以寫成KL散度那我們就恭敬不如從命吧！寫成KL散度後發現就是原始論文中所提及到的方程式 (3)了，這個就是我們的目標函數。

原始論文後面也有算法 (第13頁方程式 (17)開始)，不過有一些步驟有跳過，以上這些過程是我參考論文以及一些網站教學後，再重新計算一次的結果。這個過程相當痛苦，卻又不得不感嘆這些過程的演變，真的相當神奇。

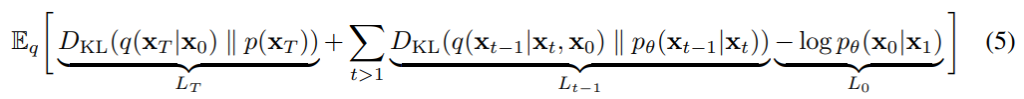
這個目標函數其中分為三個大項目： 、 、 ，這三個項目的意義分別列舉出來給各位看：

• (文章中3.1章節)：為處理先驗機率的項目，用來表示最終的雜訊輸入與常態分布的相似程度。這個部分沒有參數，計算出來為一個常數，所以對於訓練並無太大意義。可以忽略。
• (文章中3.2章節)：為處理去噪的項目，用來表示我們訓練出的神經網路與真實加噪時其分布情況的近似值，使用KL散度做為衡量兩個機率分布的距離。
• (文章中3.3章節)：是重構項目，可以使用蒙地卡羅估計法來優化這個部分。求出來的值比較小，也可以忽略。

面對大魔王，計算損失

接著根據論文，我們要來看看 了，我們可以從上面的公式跟論文中3.2章節注意到這項看起來非常重要，實際上還真的很重要XD。我們計算這個是因為要知道「前向擴散中加雜訊的那個常態分布的”平均值”與”標準差”」，這樣我們才能計算與「模型預測出來的去噪雜訊之常態分布的”平均值”與”標準差”」的「誤差」，用於後續模型優化！

我們看到這個部分裡面有一個 ，現在就要從這邊下手。根據我查到的 資料 ，他會正比於以下一長串東東。

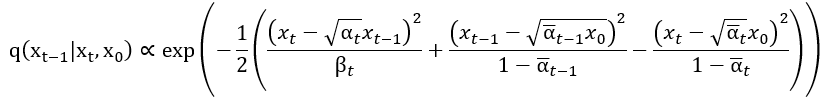
正比符號 右邊串東西把那三個分式的項目展開後通分相加並把 的部分整理一下。另外根據查到的那篇文章，它將 與 的部分當成不必要的部分處理，所以方程式變成了：

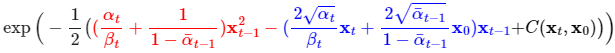
這個方程式是使用參考資料中提供的，因為我自己寫這些公式都是使用Latex，然後不知道如何改變字的顏色XD

從公式可以看到有紅紅的部分跟藍藍的部分，它分別對應 項以及 項，最後的 是代表與 跟 有關的部分，裡面與 完全無關，但因為不重要所以就簡化成這樣了~

接著我們根據機率密度函數可以知道變異數 等於前面紅色部分 常數項的倒數，也就是這樣子：

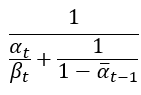
接著我們把很前面提到的 ，帶入這個公式後計算一下，方程式會變成 。這就是論文中方程式(7)的變異數的計算方法。

變異數搞定了以後我們就要來計算這個常態分布的平均值了，這平均值計算是使用藍色部分除以紅色部分而成，紅色部分剛剛算出來等於 ，所以平均值計算後會變成：

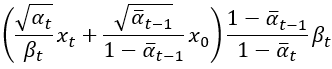
這個就是論文中方程式(7)的 ，論文中將之乘開來了。好了接著看到了 以後，相信各位也知道要來收伏筆了，前面我們算出了：

把這個帶入上式就好，接著再整理一下，這些部分都是簡單的分數化簡，所以也沒什麼技術含量，最後計算出來的結果，常態分布的平均值 就是：

好了，算出了前向擴散的期望平均值與變異數以後差不多要來終結這個東西了！

終曲，計算最後的目標函數 (損失)

接著我們要計算前向擴散雜訊常態分布的與模型預測的雜訊常態分布的誤差，也就是計算兩個平均值的誤差，接著再參數化目標函數，至於變異數論文說他們計算結果一樣，所以基本上就也不太重要了。所以我們先來看看剛剛前向擴散部分的平均值：

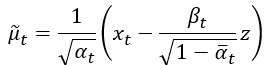
這個方程中， 就是模型的輸入，後面的 我們要把它參數化，在深度學習中，這個技巧叫做重參數化(Reparameterizing)。

接著我們要訓練的DDPM模型，他是要學習逆向擴散的，根據原始論文的方程式(1)，它的形式為：

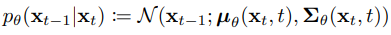
該式代表輸入 後要得到 的條件機率分布，也就是逆向擴散去噪一次的數學表達。

其中 就是逆向擴散的常態分布的平均，理想情況下它應該要與 一樣，所以 的表達式可以寫成：

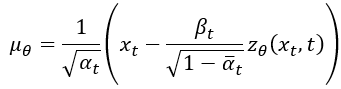
因為要來最小化 和 的誤差，所以整個損失可以寫成如下這樣，就是論文中的方程式(8)，計算方式就類似MSE (L2損失)， C 就只是一個常數而已。

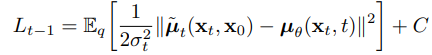
根據原始論文，作者說標準差平方，也就是變異數結果一樣，所以就沒有特別去理他了。

論文節錄圖，圖源於文章中3.2章節。

我們把剛剛算出來的 和 帶進去，之後會變成：

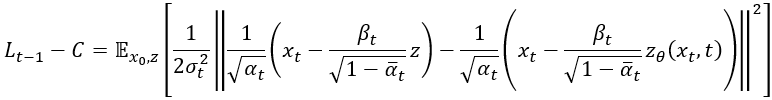
論文中使用 來代表雜訊 。那時候我在計算時並沒有注意到符號的種類就直接使用了orz，不過他們是一樣的意思~

我們將裡面的東西用分配律合併：

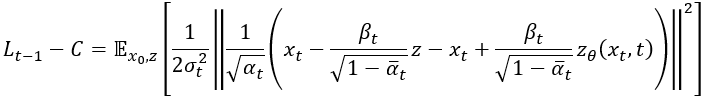
然後來消 ，接著再把 用分配律提出來，再把它與 放到外面去 (記得要平方)，所以最後就變成：

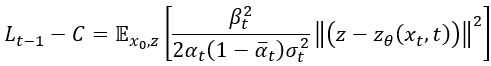
前面計算 把他帶進去就是論文中的方程式(12)了！

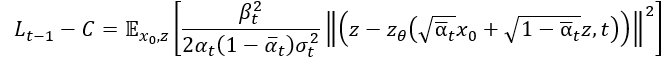
最後根據實驗表示忽略掉其權重項目，也就是前面那串分式 ，會讓訓練變的更穩定，所以整體目標函數可以簡化成這種形式。

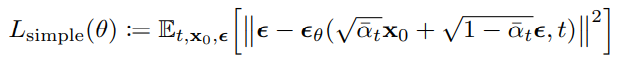
到此，所有重要的方程式都推導完畢，完結灑花。雖然這些東西較艱深難懂，不過就盡可能理解吧，我也是參考了非常多的資料以及無數的日夜動手推導才得出來這些結論的QQ。希望我的解釋能讓各位少走一點彎路~

訓練方式

論文中說明到幾個虛擬碼 (Pseudocode Code)，這些演算法告訴我們DDPM要如何實現，接下來來個別介紹文章中提到的兩個最主要的算法：

1. 訓練部分：

   訓練部分簡單分成這幾個步驟，首先從資料集中採樣一批圖片；接著隨機取一個時間步t，這個t是從1~T隨機生成的；再從平均為0變異數為1的標準常態分布中採樣一個雜訊ε；接著計算模型輸出 (如下)與ε的MSE，接著誤差經過反向傳播計算梯度並和優化器將每個權重做更新。

   

   

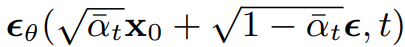
2. 採樣部分：

   這部分比較簡單，首先從標準常態分布採樣一個雜訊 ；接著重複 次，每一次要從 得到 的分布，並且採樣逆向擴散到 ；重複 次以後就會得到原始的圖片 。間單來說就是現在要從雜訊返回原圖，所以要從 這個雜訊開始一步一步去噪，最後得到乾淨的圖片 。

   

總的來說DDPM的訓練方式如下圖。主要就是分成前向擴散與逆向擴散，擴散方式的公式以及細節等就如同上面介紹的一樣：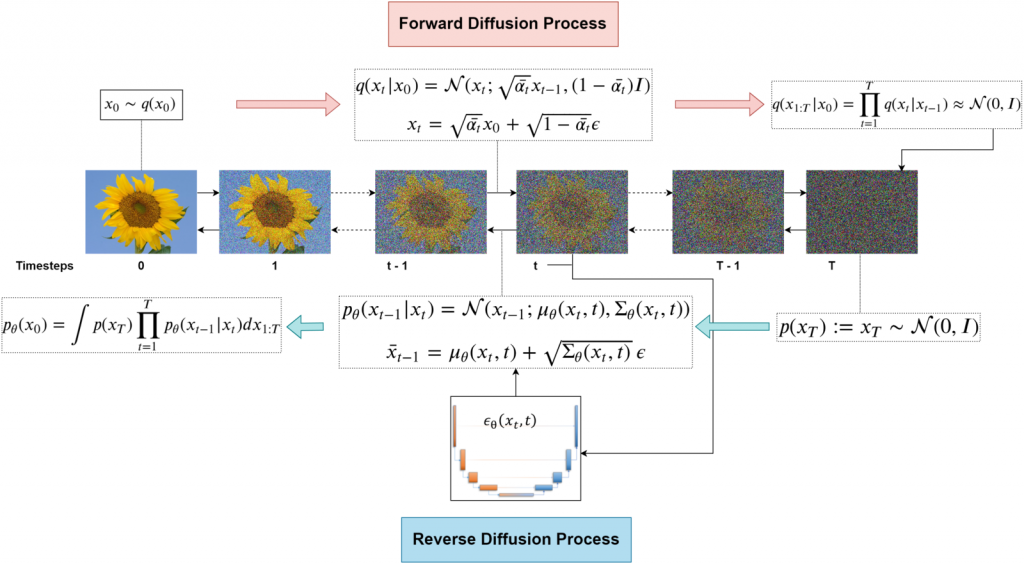

整個DDPM的訓練架構。圖源

結語

今天介紹的擴散模型其數學原理非常複雜，雖然讀過了很多次原始論文以及相關文獻，也有盡力計算論文內的公式，但可能還有一些疏漏。在這邊我會列舉出我參考的所有參考文獻，希望各位如果有搞不懂的部分可以再提出問題，雖然我很有可能也不會XD，但我會盡可能找出適合的方式解釋各位的疑問。明天會介紹DDIM，它改良了DDPM訓練久的缺點。接著就會再來實作DDIM，希望各位可以藉由這篇文章更理解擴散模型的原理😪。

Reference

DDPM-1
DDPM-2
DDPM-3
DDPM-4