[Day30]：評估生成模型優劣指標—IS & KID & FID

2023 iThome 鐵人賽

DAY 30

AI & Data

生成式AI到底何方神聖？一窺生程式AI的真面目系列第 30 篇

15th鐵人賽深度學習生成式ai 模型評估指標

golucky_sir

2023-10-03 00:11:18

3243 瀏覽

分享至

前言

這系列的文章我分享過了很多建立生成模型的辦法，但依然很難去從訓練過程看到圖片生成的品質如何，所以今天要繼續分享一些評分標準，讓各位可以比較好的幫生成模型評分！

這部分本來想搭配優化算法的，因為我在做超參數最佳化的時候常常使用這些指標當作fitness value，並讓優化算法以此更新超參數的值。但發現30天太短，有機會的話明年就來介紹優化算法的種種，敬請期待！

這些指標可以幹嘛？

今天要介紹KID與FID分數，這兩個都是在論文中很常出現的指標。這兩個指標與前一天介紹的LPIPS的共通點都是有使用深度學習的模型來輔助計算圖片的特徵。接下來就來詳細介紹一下KID與FID的細節，並使用Python建立程式。

Inception Score (IS)

這個指標是使用Inception網路來計算生成圖片分數的方法，Inception網路是已經預訓練好的圖片分類器網路。它使用ImageNet資料集來進行訓練，總計有超過百萬張照片，總計有1000的分類。這個網路架構常常被拿去做遷移學習。

Inception網路用來計算生成圖片的品質主要判斷生成圖片是否是清楚的、以及生成圖片的多樣性是否足夠。前者用來評估生成模型能力是否優秀，後者用來判斷生成模型是否有模式崩潰 (Mode Collapse)的問題發生。

對於圖片清晰程度與多樣性，IS指標是使用不同方式評估的：

清晰程度：這部分就是將圖片輸入到網路中，因為網路是分類器模型，所以模型輸出一定是1000個分類中每個分類的機率。當結果出來後，某個分類的機率很高，代表圖片夠清楚，可以讓網路很好的判斷出圖片屬於哪個類型；如果圖片很模糊的話，原則上網路很難分辨圖片是屬於甚麼分類，所以這個分類的機率差距就會不大。見下列公式的 $p(y|x)$ 。
生成圖片多樣性：多樣性的話就比較好解釋，假設一次生成1000*n張圖片，那理論上這些圖片的分類應該要是均勻分布的，也就是每張圖片都有n張，此時模型的多樣性就是最好的。當然這只是最理想的情況下，如果生成的圖片都是屬於同一種類的話，代表生成模型模式崩潰了，無法生成更多元的圖片，才會導致圖片的種類都是只有少數幾種。見下列公式的 $p(y)$ 。

IS的公式比較簡單，如下式：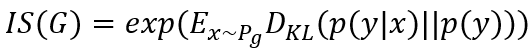

其中 $exp$ 函數似乎沒有特別含意，只是透過這個函數計算結果而已； $x~P_g$ 這代表從生成器 $P_g$ 生成圖片 $x$ ； $p(y|x)$ 代表將圖片輸入到Inception網路中得到一個機率向量 $y$ ，這個向量應該要是偏向某一個機率，可以判斷圖片的清晰度； $p(y)$ 代表將所有生成的圖片輸入到Inception網路中得到許多向量，這些向量的平均，代表生成圖片在所有類別上的邊緣分布，用於檢測多樣性。這個公式就是要對 $p(y|x)$ 與 $p(y)$ 取KL散度，KL散度在D14講過了，這邊附上公式：

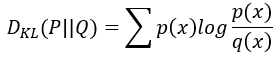
y代表圖片屬於某個類別的機率分布，因為是條件機率分布 (使用條件x得到機率y)，故使用 $p(y|x)$ 表示。

扯了一大堆，結論就是當 $p(y|x)$ 和 $p(y)$ 距離越大則代表這兩個機率分布越不相似，代表生成圖像質量越好，為何要不相似呢？剛剛有說到 $p(y|x)$ 是用來判斷圖片清晰度的，他應該要偏向某一類別，所以分布狀況應該會比較尖；而 $p(y)$ 是要判斷多樣性的，他應該要盡可能式平均分布，所以分布狀況會比較平。一個尖一個平，分布當然要很不相似啦~

IS越高代表圖片品質越好。

如何實現IS

接著進入實作了，剛剛有介紹到IS要使用模型，不過這個模型已經訓練好了，各位可以至GitHub下載模型權重檔，下載完後就可以來寫程式啦，剛剛介紹的公式可能很難寫成程式。

這個權重檔名稱為inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5，它是沒有輸入輸出層的，這意味著使用的模型只會到最後一層卷積後就輸出，該層卷積的特徵數量為2048；輸入則可以根據需求自定義。

我們可以使用InceptionV3(weights=權重檔案路徑, include_top=False, pooling='avg')來使用這個模型，權重檔案路徑就是剛剛GitHub下載的權重路徑。

在經過我的使用，如果要輸出1000維度的向量的話，必須要使用imagenet的權重 (weights=’imagenet’)，但輸入shape會被限制在(299, 299, 3)，除非使用遷移學習將輸入層調整成符合自己需求的形式，否則就是要將圖片轉成(299, 299, 3)的大小。或者可以使用上面提到的權重，並計算特徵，接著自行轉成機率的形式。程式碼如下：

from tensorflow.keras.applications import InceptionV3
import numpy as np

def calculate_IS(img):
    model = InceptionV3(weights='inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5', 
                        include_top=True, pooling='avg')
    # 計算圖片的機率分佈
    preds = model.predict(img) #注意輸出是2048長度的向量，之後FID與KID都是使用這個輸出
    probs = np.exp(preds) / np.sum(np.exp(preds), axis=1, keepdims=True)

    # 計算Inception Score
    kl = probs * (np.log(probs) - np.log(np.expand_dims(np.mean(probs, 0), 0)))
    kl = np.mean(np.sum(kl, 1))
    is_score = np.exp(kl)
    return is_score

接著就可以使用了~輸入圖片的shape要為(圖片數量, 圖片寬, 圖片高, 3)。

這個模型最大的缺點就是分類類別是固定的，所以不能甚麼圖片都餵進去！推薦分類模型—Inception網路與生成模型所使用的資料即要同源，Inception網路可以直接透過指定weights=None來載入空模型並加以訓練。所以不推薦真的使用於評估上，但它作為FID與KID的基礎，其重要性依然不容忽視。

另外，因為他沒有與真實資料進行比對，所以出來的結果會與人的感覺不接近，所以接下來要來介紹FID與KID，這兩個都是基於IS並改良，使其更符合人類的感知。

Fréchet Inception Distance (FID)

接著換FID分數了，這個分數真的是最廣泛運用在各個圖片生成任務的指標。D26介紹的DDIM，作者也有使用FID分數來評估模型能力，那個個指標到底哪裡好用呢？接下來就來看看FID分數吧。

FID分數也是基於使用Inception網路的一個生成模型評估指標，他可以計算真實圖片與生成圖片的特徵向量之間的距離。距離近也就是分數低則相似度高，反之亦然，兩張圖片一模一樣則FID=0。FID的Fréchet Distance其實就跟Wasserstein Distance類似，全名叫做Wasserstein-2 Distance，對多了一個2而已XD。

FID的公式如下：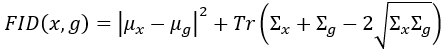

其中x代表真實圖片經過Inception網路計算出特徵的平均值； $g$ 代表生成圖片經過Inception網路計算出特徵的平均值； $\mu$ 代表平均值； $\sum$ 代表共變異數； $Tr$ 代表計算方陣 (n*n矩陣)的跡數 (trace)也就是方陣中主對角線的元素總和。

FID更適合評分生成模型的多樣性，但是他基於特徵提取，所以並不會考慮特徵位置的合理性，例如今天做動漫人臉生成，如果生成的鼻子在嘴巴下方，FID的分數也會很低，而認為這張動漫人臉的照片很棒。

FID值越低代表圖片質量越好。

如何實現FID

接著輪到程式實作的部分了。FID的公式看起來比較簡單，可以使用numpy去計算大部分的部分、唯有開根號的 $\sqrt{\sum_x\sum_g}$ (幾何平均)需要使用scipy.linalg.sqrtm來計算。完整程式如下：

輸入特徵格式是(n, 2048)，n代表特徵數量，需要大於1。

import numpy as np
from scipy import linalg
from keras.applications.inception_v3 import InceptionV3
from keras.applications.inception_v3 import preprocess_input

def get_features(images): #計算圖片特徵
    model = InceptionV3(weights='inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5', include_top=False, pooling='avg')
    # 預處理圖片，將其轉換為Inception v3模型的輸入格式
    images = preprocess_input(images)
    features = model.predict(images)
    return features
def calculate_FID(features_x, features_g):
    # 根據公式，x代表真實圖片，g代表生成圖片
    # 計算真實圖片和生成圖片之特徵向量的平均值和共變異數矩陣
    # 平均值
    mu_x = np.mean(features_x, axis=0)
    mu_g = np.mean(features_g, axis=0)
    # 共變異數矩陣
    sigma_x = np.cov(features_x, rowvar=False) #shape=(2048, 2048)
    sigma_g = np.cov(features_g, rowvar=False)
    # 平均值之間的平方距離(square distance)
    square_distance = np.sum((mu_x - mu_g) ** 2)
    # 共變異數矩陣的幾何平均
    covariance_mean = linalg.sqrtm(sigma_x.dot(sigma_g))
    # 有些元素可能平方過後變成複數，所以要把複數都取實部
    if np.iscomplexobj(covariance_mean):
        covariance_mean = covariance_mean.real
    fid = square_distance + np.trace(sigma_x + sigma_g - 2*covariance_mean)
    return fid
features_x = get_features(img_real) #圖片的shape為 (n, 圖片寬, 圖片高, 3)
features_g = get_features(img_fake)
fid = calculate_fid(features_x, features_g)
print('FID between img1 and img2 is:', fid)

Kernel Inception Distance (KID)

KID距離也是使用Inception網路建立的評估算法，它可以透過計算Inception網路出來的圖片特徵之間的平均值差異的平方，來衡量兩個特徵之間的差異。另外KID有一個三次核的無偏估計值，這個東東能夠與我們的感知更加相近。其實KID就是Inception網路計算出來之特徵向量空間的多項式核函數平方MMD，好我知道名字很長聽起來超難，所以我們先來看看最大平均差異 (Maximum Mean Discrepancy, MMD)，接著再來慢慢剖析KID。

最大平均差異MMD？

你可能會覺得很奇怪，怎麼突然跑出了這個東西，MMD是KID的核心，所以必須了解它，了解它才能了解KID。

MMD是一種積分機率衡量方法，它可以衡量兩個相關機率分布的距離。要完整介紹勢必會花費非常長的篇幅，所以我會簡單介紹MMD。首先MMD是要尋找一個函數f，計算不同分布的特徵向量樣本在經過函數 f 計算後函數值的平均值，把P與Q的平均值相減就可以得到兩個分布對應到函數f的平均差異(Mean Discrepancy, MD)。MMD多了一個Maximum，想必就是用來尋找能夠使MD達到最大值的 f 了。為了不要讓 f 變的無法無天，所以添加了一個限制—再生希爾伯特空間 (Reproducing Kernel Hilbert Space, RKHS)。此時MMD的公式就如下方公式：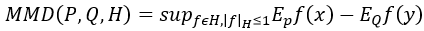

其中P是生成圖像分布；Q是真實圖像分布；H是希爾伯特空間 (Hilbert Space)。整個公式翻譯成中文就是：

我們希望找到一個f，這個 f 期望兩個分布 ( $E_pf(x)$ 與 $E_qf(y)$ )的動差 (moments)相減能夠最大 (求得最小上界 sup)。其中 f 屬於希爾伯特空間 f∈H，且限制在再生希爾伯特空間裡 |f|≤1 的單位球中。

接下來呢？當然就是推導公式，將公式展開使其在計算層面上比較好理解，就算不理解也能比較容易的寫成程式XD，至少不會像上式，幾乎看不出來要怎麼計算。接下來的推導我都是參考這個網頁的資料。

首先翻譯完公式之後，我們從名字最炫的再生希爾伯特空間下手，因為它在希爾伯特空間裡面，所以可以使用**里斯表示定理 (**Riesz's Representation theorem)將期望改寫成希爾伯特空間的內積形式：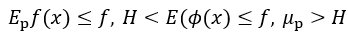

$\mu_p$ 就是Mean Embedding了！此時MMD可以再被翻譯成計算兩個分布在某個空間中Mean Embedding的距離，為了使這個距離最大，所以將內積變成範數 (在希爾伯特空間中範數就是內積)，然後在再生希爾伯特空間中內積可以使用核 (kernel)計算，有了這些步驟以後整個公式可以變成平方MMD的表達式。

得到了表達式所以呢？

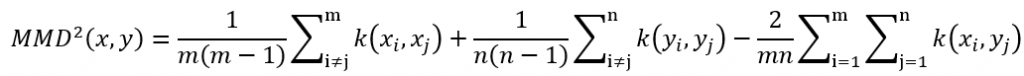
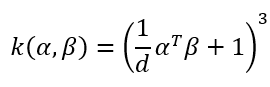
天啊這公式超長的，但是只要有 $\sum$ 就可以用迴圈、Numpy等來計算，非常簡單。其中m是生成圖片的數量；n是真實圖片的數量；k就是核 (kernel)，計算方式如上，d為向量維度，在此等於2048。另外這些東東告訴我們KID就是特徵向量空間的多項式核函數平方MMD，也就是說剛剛那條又臭又長的表達式中每個x跟y就是來自於Inception網路計算出來的長度為2048的向量 (也就是d)，另外kernel的計算方式也如上。

KID的值越低代表圖片值量越好。

如何實現KID

KID距離的實現我是直接使用這段程式碼改寫而成，注意變數m與n分別代表圖片樣本量與特徵向量長度(d)，與上述表達式不同。程式的實現方式有很多種，只要能夠正確計算出就好，接著再來考慮如何使用最少時間計算出結果即可。

程式碼有些複雜，希望各位可以根據上面給的公式盡可能的理解：

import numpy as np
from keras.applications.inception_v3 import InceptionV3
from keras.applications.inception_v3 import preprocess_input

def get_features(images): #計算圖片特徵
    model = InceptionV3(weights='inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5', include_top=False, pooling='avg')
    # 預處理圖片，將其轉換為Inception v3模型的輸入格式
    images = preprocess_input(images)
    features = model.predict(images)
    return features
def calculate_KID(real_features, generated_features, num_subsets=100, max_subset_size=1000):
    n = real_features.shape[1]
    m = min(min(real_features.shape[0], generated_features.shape[0]), max_subset_size)
    t = 0
    for _subset_idx in range(num_subsets):
        #隨機挑選一張圖片
        x = generated_features[np.random.choice(generated_features.shape[0], m, replace=False)]
        y = real_features[np.random.choice(real_features.shape[0], m, replace=False)]
        #計算各部分的核(kernel) @代表內積
        a = (x @ x.T / n + 1) ** 3 + (y @ y.T / n + 1) ** 3
        b = (x @ y.T / n + 1) ** 3
        t += (a.sum() - np.diag(a).sum()) / (m - 1) - b.sum() * 2 / m
    kid = t / num_subsets / m
    return kid