接下來我們在這裡要介紹一些比較雜的演算法像是Floyd Warshall algorithm, minimum spanning tree(MST), Kruskal algorithm 還有 Prim’s algorithm。

Floyd Warshall algorithm

Floyd Warshall algorithm 可以用來計算任意兩點間的最短距離，它跟Bellman-Ford一樣無法用在有negative cycle的圖，但它也無法偵測圖是否有negative cycle。如果你看它的程式碼，它有點像是用窮舉的方法不斷做比較，見以下圖說明: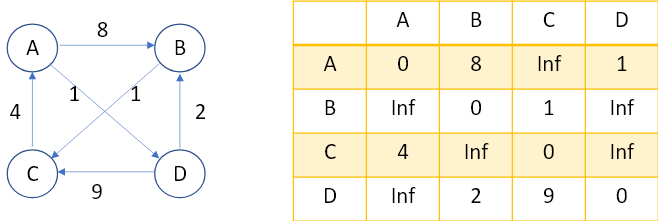

圖1，假設今天我們有個路徑如左圖，我們想用Floyd-Warshall找到任意兩點間的最短距離，首先我們將左圖改寫成如右圖的陣列。若兩點間無直接通往的箭頭者，我們用Inf代替; 自己到自己距離為0，故對角線為0。
接著我們要試著藉由更新陣列，算出兩兩點間的最短距離，舉例來說: AB=8，會拿他和AA+AB=8, AB+BB=8,AC+CB=Inf,AD+DB=3做比較，這裡我們發現3小於8，所以我們Array[A][B]更新為3。以此類推，直到整個陣列更新完畢，時間複雜度O(V^3)(三層loop)，空間複雜度O(V^2)(創了VxV)的陣列。我們直接來看個程式碼:

import numpy as np

def FloydWarshall(graph):
    numV = len(graph)
    for i in range(numV):
        for j in range(numV):
            for k in range(numV):
                graph[j][k] = min(graph[j][k], graph[j][i]+graph[i][k])
    return graph

G = np.array([[0, 8, float('Inf'), 1], [float('Inf'), 0, 1, float('Inf')], [
    4, float('Inf'), 0, float('Inf')], [float('Inf'), 2, 9, 0]])

print(FloydWarshall(G))
>>   [[0. 3. 4. 1.]
     [5. 0. 1. 6.]
     [4. 7. 0. 5.]
     [7. 2. 3. 0.]]

Minimum spanning tree(最小生成樹)

最小生成樹為樹的一個子集合，其邊(edges)是互相連結節點、沒有方向性、有權重，所有vertices連在一起、不會形成一個cycle(封閉循環)，然後所有邊的權重加起來為最小。實際的例子譬如說，有五個獨立的小島，你要在島和島中間蓋橋，是得五個島相連，但蓋橋成本最低。(課程中的例子)那在那之前，要先介紹一下disjoint set(併查集): Disjoint set 為一資料結構，用來幫助追蹤元素集，這些元素集被劃分為許多不相交且不重疊的集，並且每個集都有代表(幫助識別該集)，常用來檢測圖是否相連。它有幾個功能:
MakeSet(x)：創建一個包含單個元素x的新集合。
Union(x,y): 將包含x的集合與包含y的集合合併。
Find(x): 確定特定元素x屬於哪個幾何並返回屬於x所在集合的代表元素。

class DisjointSet:
    def __init__(self, vertices):
        self.vertices = vertices
        self.parent = {}
        for i in vertices:
            self.parent[i] = i
        self.rank = dict.fromkeys(vertices, 0)
    # 尋找你要找的element屬於那個子集合
    def find(self, x):
        if self.parent[x] == x:
            return x
        else:
            return self.parent[x]

    def union(self, x, y):
        xroot = self.parent[x]
        yroot = self.parent[y]
        # 比較他們的rank，比較大的併別人
        if self.rank[xroot] > self.rank[yroot]:
            self.parent[yroot] = xroot
        elif self.rank[xroot] < self.rank[yroot]:
            self.parent[xroot] = yroot
        else:
            # 一開始沒有大小差別讓xroot變mother
            self.parent[yroot] = xroot
            self.rank[xroot] += 1

if __name__ == '__main__':
    vertices = ['A', 'B', 'C', 'D', 'E', 'F']
    ds = DisjointSet(vertices)
    ds.union('A', 'B')
    ds.union('A', 'E')
    # 來看E屬於哪個集合
    print(ds.find('E'))
    print('===check the parent dictionary===')
    print(ds.parent)

# E的集合
>>  'A'
  ===check the parent dictionary===
 {'A': 'A', 'B': 'A', 'C': 'C', 'D': 'D', 'E': 'A', 'F': 'F'}

好惹，接著我們來看怎麼用Kruskal和Prim algorithm解最小生成樹。

Kruskal algorithm

Krusal algorithm是一種貪婪算法(greedy algorithm)，用來算加權無向圖(weighted undirected graph)的最小生成樹。首先將每個節點用disjointset變成一個個set，然後將他們根據權重(weight)由小到大排序，然後由小到大union兩兩節點N-1次(當他們不屬於同一個union時)，即可得解，我們來看程式碼可能比較快:

import DisjointSet as dst

class Graph:
    def __init__(self):
        self.numV = 0
        self.graph = []
        self.MST = []
        self.vertices = []

    def add_edge(self, s, d, w):
        self.graph.append([s, d, w])

    def add_node(self, v):
        self.vertices.append(v)
        self.numV += 1

    def KruskalAlgo(self):
        i, c = 0, 0
        ds = dst.DisjointSet(self.vertices)
        self.graph = sorted(self.graph, key=lambda x: x[2])
        while c < self.numV-1:
            s, d, w = self.graph[i]
            i += 1
            x = ds.find(s)
            y = ds.find(d)
            if x != y:
                self.MST.append([s, d, w])
                ds.union(x, y)
                c += 1
        res = ''
        for s, d, w in self.MST:
            res += f'{s}-{d}:{w}'
            res += '\n'
        print(res)


g = Graph()
g.add_node('A')
g.add_node('B')
g.add_node('C')
g.add_node('D')
g.add_node('E')
g.add_edge('A', 'B', 5)
g.add_edge('A', 'C', 13)
g.add_edge('A', 'E', 15)
g.add_edge('B', 'A', 5)
g.add_edge('B', 'C', 10)
g.add_edge('B', 'D', 8)
g.add_edge('C', 'E', 20)
g.add_edge('C', 'A', 13)
g.add_edge('C', 'B', 10)
g.add_edge('C', 'D', 6)
g.add_edge('D', 'C', 6)
g.add_edge('D', 'B', 8)
g.add_edge('E', 'A', 15)
g.add_edge('E', 'C', 20)
g.KruskalAlgo()

Prim's Algorithm

Prism’s algorithm也是一種解加權無向圖(weighted undirected graph)的最小生成樹的貪婪演算法。首先，先任意選擇一個節點作為起始點，並將之標為visited，觀察周圍的邊，找最小權重者，選擇最小邊到達的點，標為visited，將此段存於MST list中，再找下一個連結的最小邊，再將之到達的點標為visited，以此類推直到所有節點都visited。這個影片解釋得不錯，才兩分鐘，可以參考一下: https://www.youtube.com/watch?v=cplfcGZmX7I
直接來看程式碼:

import sys
class graph:
    def __init__(self, node, edges):
        self.node = node
        self.edges = edges
        self.MST = []
        self.vnum = len(self.node)
    # time complexity: O(V^3), space complexity: O(V)
    def primsalgo(self):
        visited = [0]*self.vnum
        visited[0] = True
        c = 0
        while c < self.vnum-1:
            min = sys.maxsize
            for i in range(self.vnum):
                if visited[i]:
                    for j in range(self.vnum):
                        if ((not visited[j]) and (self.edges[i][j])):
                            if min > self.edges[i][j]:
                                min = self.edges[i][j]
                                s = i
                                d = j
            self.MST.append([self.node[s], self.node[d], self.edges[s][d]])
            visited[d] = True
            c += 1

        res = ''
        for s, d, w in self.MST:
            res += f'{s}->{d}:{w}\n'
        return res


edges = [[0, 10, 20, 0, 0],
         [10, 0, 30, 5, 0],
         [20, 30, 0, 15, 6],
         [0, 5, 15, 0, 8],
         [0, 0, 6, 8, 0]]
nodes = ['A', 'B', 'C', 'D', 'E']
g = graph(nodes, edges)
print(g.primsalgo())
>>
    A->B:10
    B->D:5
    D->E:8
    E->C:6

參考資料:
http://alrightchiu.github.io/SecondRound/minimum-spanning-treeintrojian-jie.html
The Complete Data Structures and Algorithms Course in Python (from Udemy)