學習率 ( Learning Rate ) 是梯度下降優化算法中的一個重要 超參數,它決定了在每一步更新模型參數時,參數應該調整多少。學習率的選擇對於優化算法的效果和速度都有顯著影響。
學習率的大小影響模型參數更新的步伐,較大的學習率可以讓模型快速的收斂,如何的去操控學習率對訓練模型的性能與速度都有很大的影響。
通常在模型訓練過程中,會根據模型結果的收斂狀況來調整學習率,而學習率的初始值會根據經驗或超參數搜索進行選擇,然後在訓練過程中進行調整,較常見就是用學習率衰減(Learning Rate Decay)方法,即在訓練過程中逐漸降低學習率,以平衡快速收斂和穩定性之間的關係,另一種方法是使用自適應學習率優化器(如 Adam、Adagrad 等 …),這些優化器可以在模型訓練過程當中去適應模型並自動調整學習率以達到最佳的收斂效果。
每種策略下的學習率效果都不一樣,以下是針對模型的學習率在不同情況或者需求下會採用的策略 :
學習率衰減是一種調整學習率的技術,用於在訓練過程中逐漸降低學習率。那為甚麼讓學習率逐漸衰退呢?可以想像當參數到達最佳解的附近時,有可能因為學習率大導致下一步移動幅度大,參數會移動至別處而跳過最佳解的地方,因此就要學習率在參數逐漸接近最佳解的過程中逐漸減小,從而幫助模型更好地收斂到最佳解
定期衰減的衰減公式:
學習率 = 初始學習率 * 衰減因子 ^ ( 迭代次數 // 衰減間隔 )
其中:
定期衰減方法在訓練的固定衰減間隔內降低學習率,通常是在訓練的特定週期或次數之後。像是你可以設定每隔幾個 epoch 就將學習率降低一定比例,隨著訓練的進行,衰減因子的幾次冪次方使得學習率不斷減小,這有助於模型在訓練後期更穩定地收斂。而實際應用中可能需要根據問題和模型的特點來調整初始學習率、衰減因子和衰減間隔,以達到最佳的訓練效果。
指數衰減的衰減公式 :
學習率 = 初始學習率 * e^( -k * 迭代次數 )
其中:
指數衰減的特點是,隨著迭代次數的增加,學習率以指數方式遞減,讓學習率不斷減小。這可以幫助模型在訓練過程中更精細地調整參數,從而提高訓練效果。
1/t 衰減的衰減公式:
學習率 = 初始學習率 / ( 1 + k * 迭代次數 )
其中:
1/t 衰減的特點是,隨著迭代次數的增加,學習率逐漸減小,但不會變為零。這種策略可以幫助模型在訓練過程中逐漸穩定,更好地收斂到最佳解。
import numpy as np
# 設定初始學習率、衰減因子、衰減間隔和訓練的總迭代次數
initial_learning_rate = 0.1
decay_factor = 0.5
decay_steps = 10
decay_rate = 0.1
num_epochs = 50
def step_decay(initial_lr, decay_factor, decay_steps, num_epochs): # 定期衰減
lr_step_decay = []
for epoch in range(num_epochs):
lr_step_decay.append(initial_lr * (decay_factor ** (epoch // decay_steps)))
return lr_step_decay
def exponential_decay(initial_lr, decay_rate, num_epochs): # 指數衰減
lr_exponential_decay = []
for epoch in range(num_epochs):
lr_exponential_decay.append(initial_lr * np.exp(-decay_rate * epoch))
return lr_exponential_decay
def inverse_time_decay(initial_lr, decay_rate, num_epochs): # 1/t衰減
lr_inverse_time_decay = []
for epoch in range(num_epochs):
lr_inverse_time_decay.append(initial_lr / (1 + decay_rate * epoch))
return lr_inverse_time_decay
# 取得在不同策略下的學習率串列
lr_step_decay = step_decay(
initial_learning_rate,
decay_factor, decay_steps,
num_epochs
)
lr_exponential_decay = exponential_decay(
initial_learning_rate,
decay_rate,
num_epochs
)
lr_inverse_time_decay = inverse_time_decay(
initial_learning_rate,
decay_rate,
num_epochs
)
# 繪出不同策略下的學習率衰退曲線
plt.plot(range(1, 51), lr_step_decay, label='step decay')
plt.plot(range(1, 51), lr_exponential_decay, label='exponential decay')
plt.plot(range(1, 51), lr_inverse_time_decay, label='inverse time decay')
plt.legend()
plt.show()
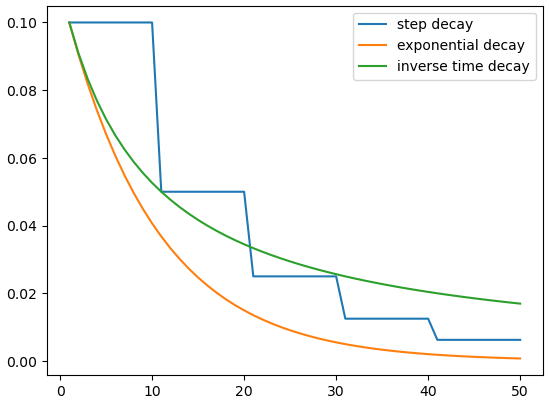
可發現隨著迭代次數的增加,指數衰減和 1/t 衰減對於學習率衰退的收斂表現較定期衰退來的好,這些策略的選擇取決於你的模型和資料,不同的方法可能對不同的問題效果更好。在實際使用中,你可以根據模型結果來調整衰減參數以及策略的抉擇。
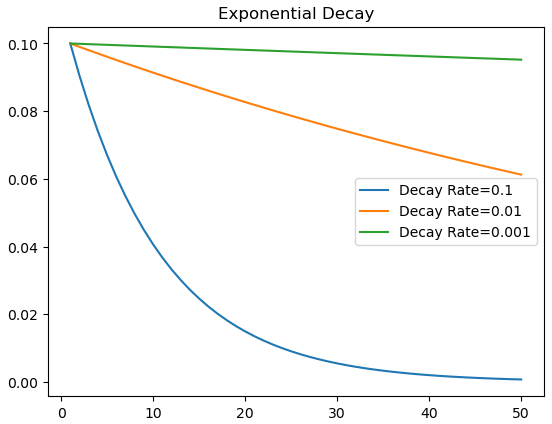
衰退因子的大小對於學習率下降的幅度有一定程度的影響,下面是進行指數衰退時用三種不同衰減因子得出的曲線。
最簡單的方法是固定學習率,但需要謹慎選擇初始值,避免過小或過大。
一些優化算法,如 Adagrad、Adadelta、Adam 等,會根據梯度的歷史大小調整學習率,從而在訓練的過程中自動適應不同參數的變化從而調整學習率。
設定學習率是一個挑戰性的任務,需要通過實驗進行嘗試和調整。常見的會用網格搜索(Grid Search)或隨機搜索(Random Search)等方法,在一個範圍內測試不同的學習率值以找出最佳的超參數 ( 包含學習率 ) 組合,藉此評估模型的性能,對於複雜的模型和問題,可以使用交叉驗證等方法來搜索最佳學習率,以找到能夠在合理時間內達到最佳性能的學習率。
下面兩張圖就是比較學習率的大小對參數的移動造成的影響,不同的學習率就會有不同的參數移動路徑,會發現到太大的學習率 ( 下右圖 ) 會導致參數來回震盪,每次移動 ( 每走一步 ) 的幅度過大而始終無法到達最低點處,但太小的學習率 ( 下左圖 ) 就好比每走一步就只走一點點,走到最低點花的時間太長,會讓整個最佳化參數的過程 ( 模型訓練 ) 相當耗時。
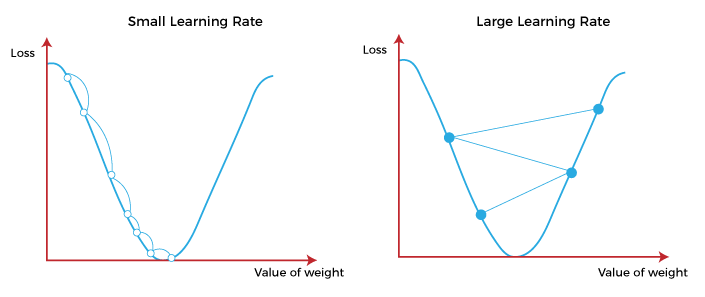
總之,在訓練模型時,學習率的調配方法必須要慎重考量,不同的方法在不同情況下可能表現不同。需考慮到問題的複雜性、數據集的大小、模型的架構等因素。在實際應用中,通常需要通過實驗和監控訓練過程來選擇最適合的學習率調整策略,以達到優化模型的效果。
今天我們學到:
了解到了學習率的作用後,那到底我們在機器學習中說的參數 ( Parameter ) 是什麼,那什麼又是超參數 ( Hyperparameter ),兩者之間到底存在什麼樣的差異,這個部分我們會在明天介紹到,那我們就下篇文章見 ~
https://www.javatpoint.com/gradient-descent-in-machine-learning
