Hi 大家好，今天要來先簡單介紹graph這個資料結構。

首先，我們前面的文章所介紹的linked list、 binary tree都可以看成是一種狹義的Graph（或著說成Graph的subset）。而Graph的定義可以更加的無拘無束，只要擁有節點（可以是某個資料結構），並且節點可以連結到別的節點，不管是會產生cycle或是有孤立的節點都沒關係。

在coding interview上，最常看到和Graph有關或是用來代表graph的兩種形式分別是：

• Adjacency List
• Matrix

今天會先談談Adjaceny List，因為matrix的題目會在下下篇才講到。

Adjacency List

其實還有另一種方式可以代表Graph就叫Adjacency Matrix，但是既然都叫matrix了，代表他需要利用二維陣列來表示Graph，相對的浪費空間。若是以Python coding時，我們可以直接利用hash map的key-value pair來代表某個節點連向了其他哪些節點。

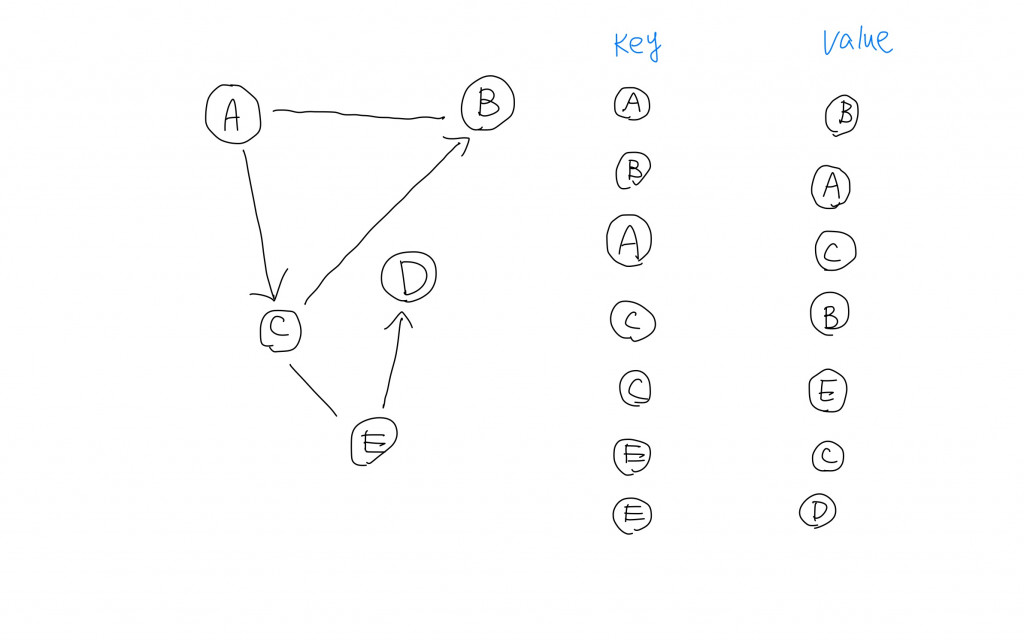
上圖將節點以key-value pair的形式表現。除此之外，可以注意到左側的圖有箭頭的edge代表只能從某個節點到達另一個節點；沒有箭頭的edge代表是雙向的。

在Python中，我們利用Dictionary來實現hashmap的功能，但是我們可以更近一步的將key-value pair的value定義成list型態，這樣可以一次表示key會對應到哪些value。若key沒有對應的value則會是empty list。

我們可以從collections去import defaultdict，並且將defaultdict設定為list型態來達成。
通常coding interview會給予我們的就是一組、一組的節點代表他們相連，這時候只要利用defaultdict和一個for回圈就可以創建出adjacency list。

from collections import defaultdict

edges = [['A', 'B'], ['B', 'A'], ['A', 'C'], ['C', 'B'], ['C', 'E'], ['E', 'C'], ['E', 'D']]

adjList = defaultdict(list)
for src, dst in edges:
    adjList[src].append(dst)

如何在adjacency list上去拜訪各節點

在拜訪tree的節點時我們通常有兩種方式：DFS和BFS，而在Graph上也是。

1. DFS（深度優先）
   有一個當作起點的節點，我們會以遞迴的方式去拜訪和他相連的節點，再以這個節點為新的起點繼續去拜訪和他相連的節點，為了不要拜訪已經在之前就拜訪過的節點，需要去紀錄已拜訪過的節點。以下的示意圖將最初的起點以紅色勾勾標註，並且依造時間點去標記拜訪的節點。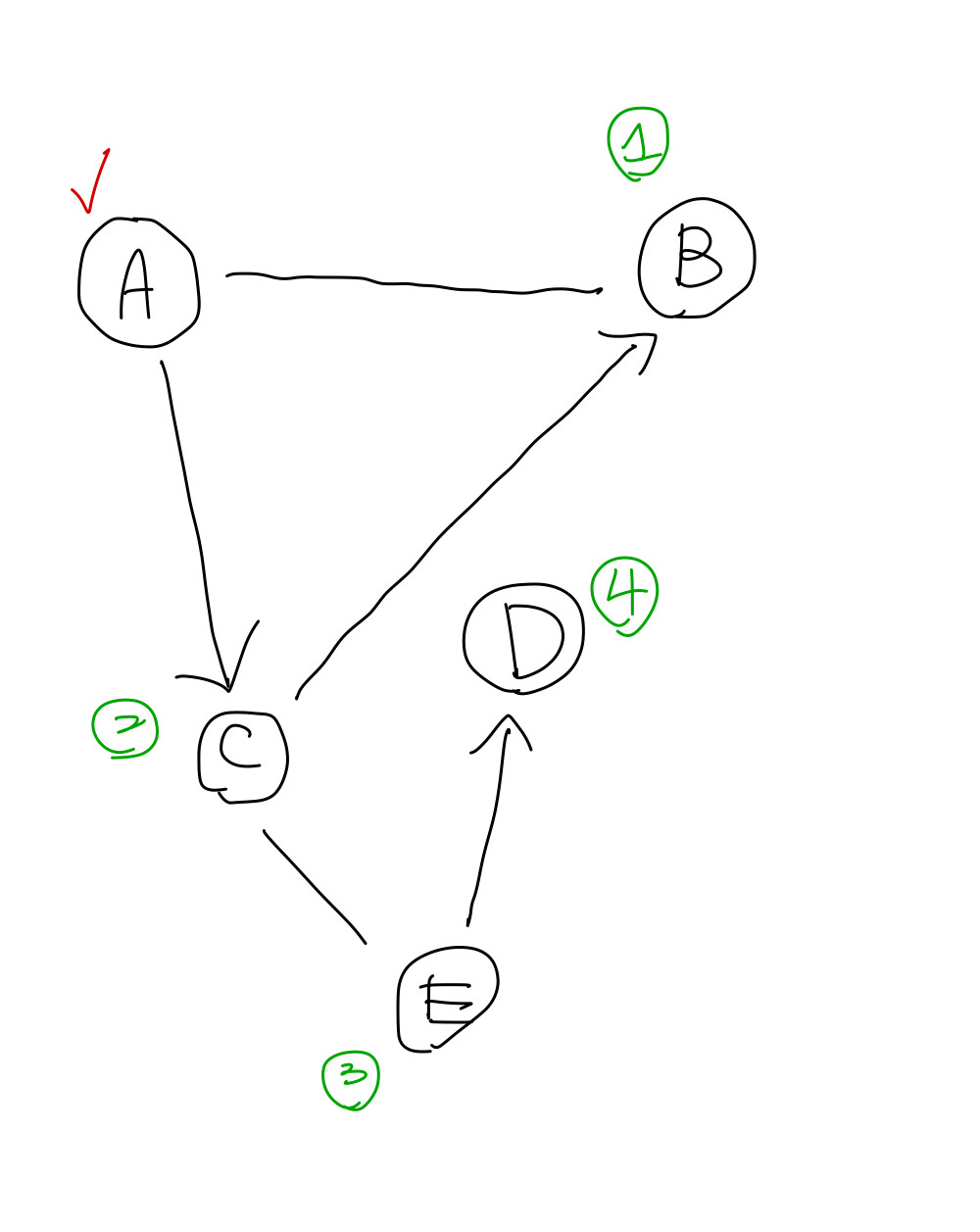
   

   def dfs(node, adjList, visit):
       if node in visit:
           return
   
       print(node)
       visit.add(node)
       for neighbor in adjList[node]:
           dfs(neighbor, adjList, visit)
   

2. BFS（廣度優先）
   有一個當作起點的節點會被放到Queue（先進先出的資料結構），當某個節點從Queue被排出來，會將和這個節點相連並且還沒被拜訪過的節點都放進Queue中。並且繼續將節點從Queue中排出。依此繼續直到Queue中沒有節點。在以python coding時，我們會從collections import deque來實現Queue。
   在下圖中，以A為起點並且會將B, C都放入Queue中，代表他們是同一個時間點被拜訪的。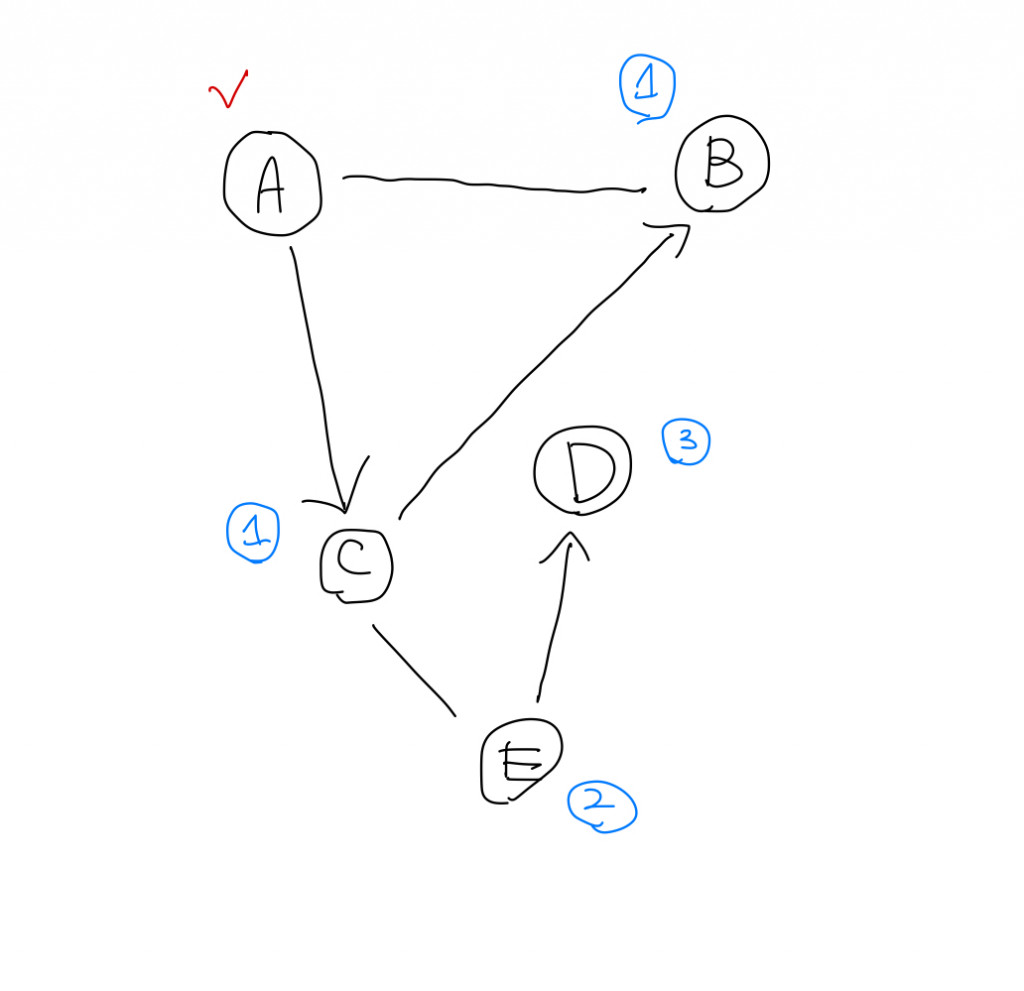
   

   from collections import deque
   
   q = deque()
   q.append('A')
   visit = set()
   level = 1
   print('-' * 10)
   
   while q:
       tmp = level
       for _ in range(tmp):
           node = q.popleft()
           print(node)
           visit.add(node)
           level -= 1
           for neighbor in adjList[node]:
               if neighbor not in visit and neighbor not in q:
                   q.append(neighbor)
                   level += 1
       print('-' * 10)
   

謝謝鐵人賽每天都讓我有產能😂