今天要繼續專研和Greedy策略相關的演算法，這次我們把Greedy應用在另一個很經典的問題上: Minimum Spanning Tree。首先我們要回歸到樹的定義，廣義的樹的定義不像binary tree，只要節點中不會出現迴圈、所有的節點都可以從某節點到達另一個節點，即n個節點會有n - 1條edge就是一顆樹。

什麼是spanning tree

spanning tree就是從沒有指向性的圖上（有n個節點），選取n - 1條edge，並且符合樹的定義，就是所謂的spanning tree。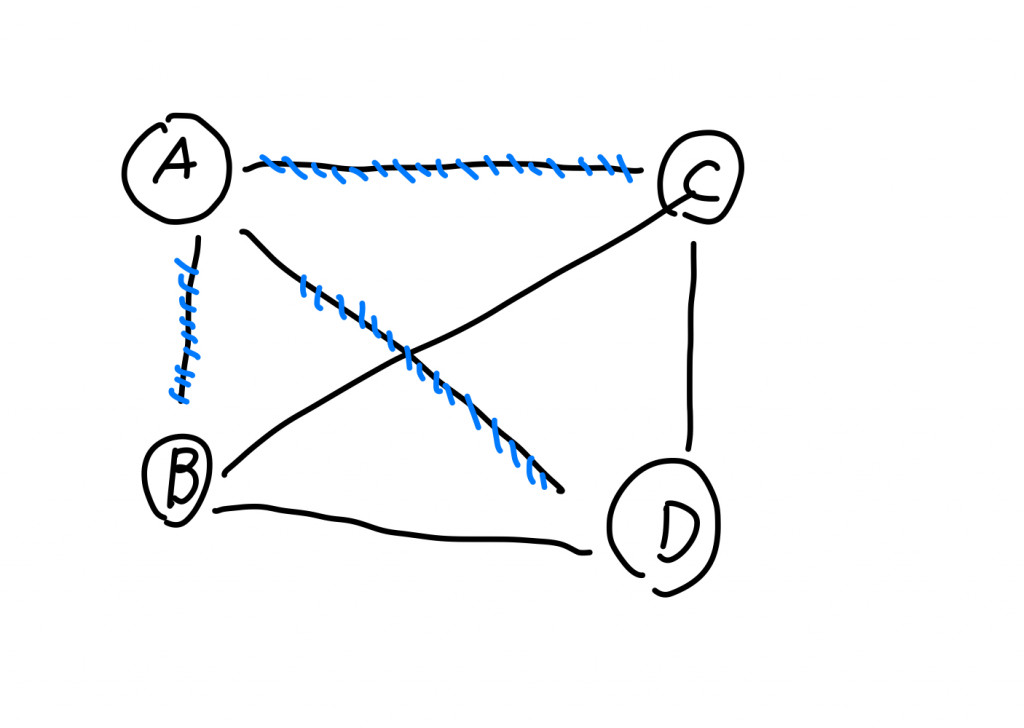

如上圖有4個節點，我們從所有的edge中選出3個節點，來形成一個樹（圖有點醜，請見諒😅）。

那如果今天我們的無向圖的每個edge都是有權重的，我們想要找出一顆spanning tree他的edge所形成的總權重是最小的，即找出minimum spanning tree。

如何找出minimum spanning tree

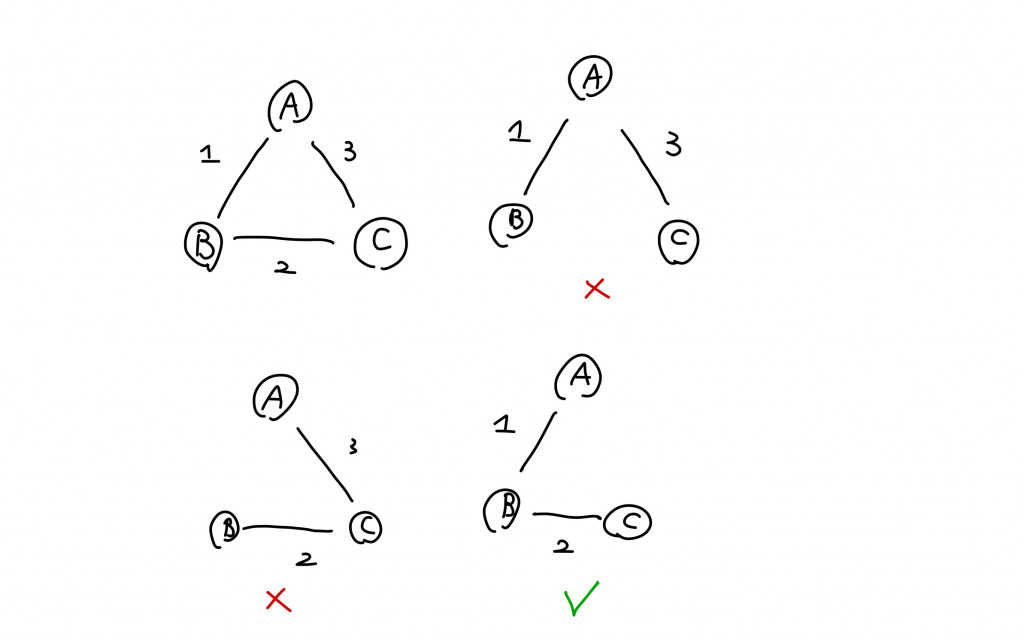
分析：
我們可以利用找出最短距離類似的方法(https://ithelp.ithome.com.tw/articles/10330059)來找出。
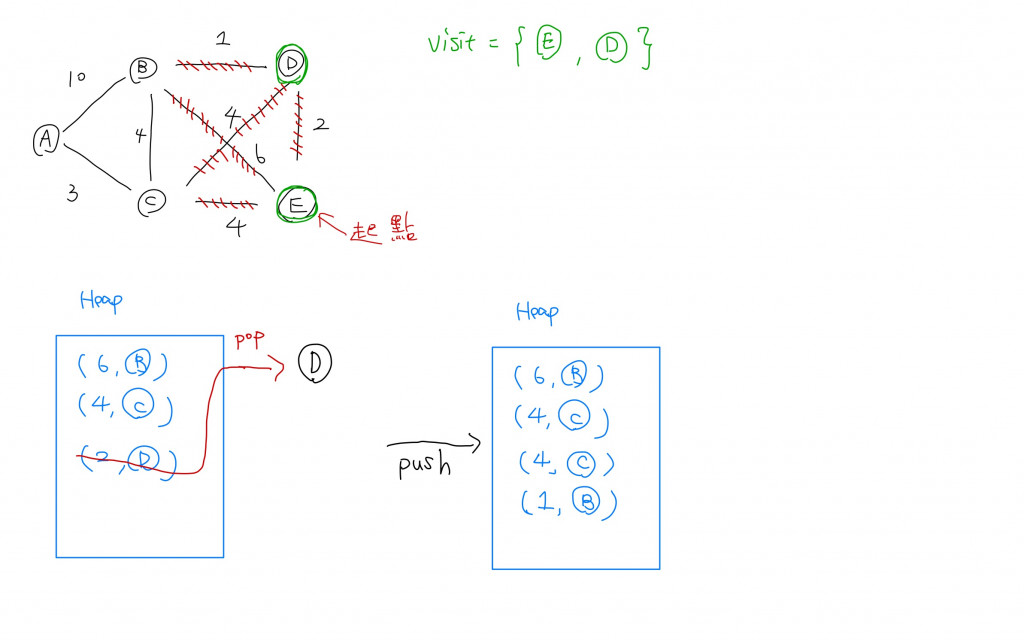
首先我們需要將任一一個節點當作起始點，我們需要將(0, 起點的位置)放入到minimum heap中，0代表目前的總權重還是0，等到我們將這個tuple從heap pop 出來後，我們會根據這個節點和哪些節點相連，把其他節點也放進到heap中，依此類推。所以我們需要一個while 迴圈。而while 迴圈的終止條件是我們拜訪過所有的節點，所以我們還需要一個set去紀錄已經拜訪過哪些節點。

接下來我們直接看看leetcode上面的題目

Leetcode 1584. Min Cost to Connect All Points

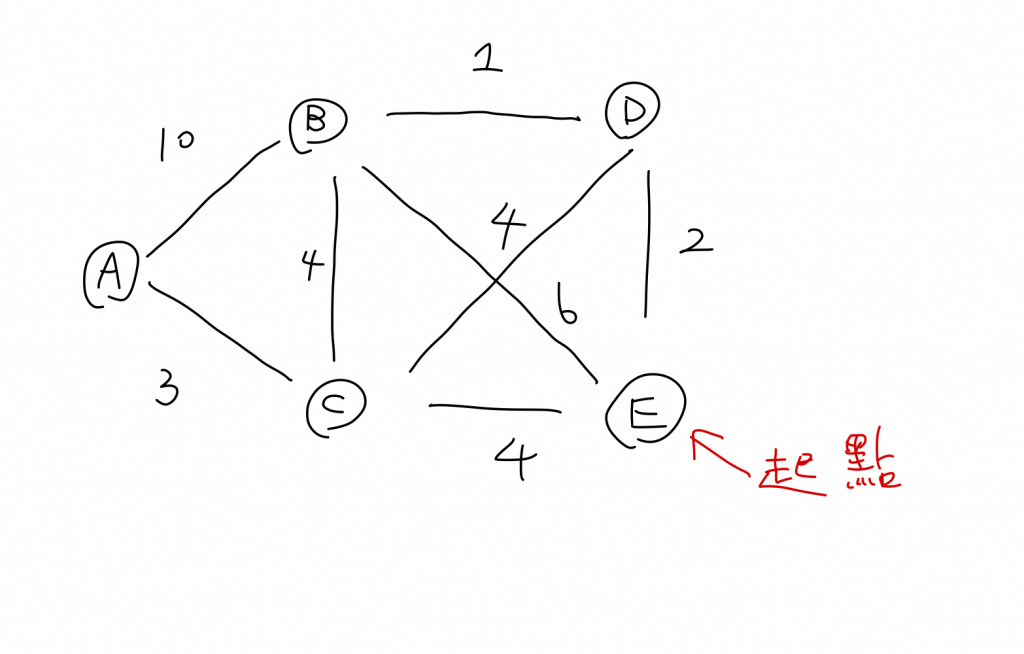
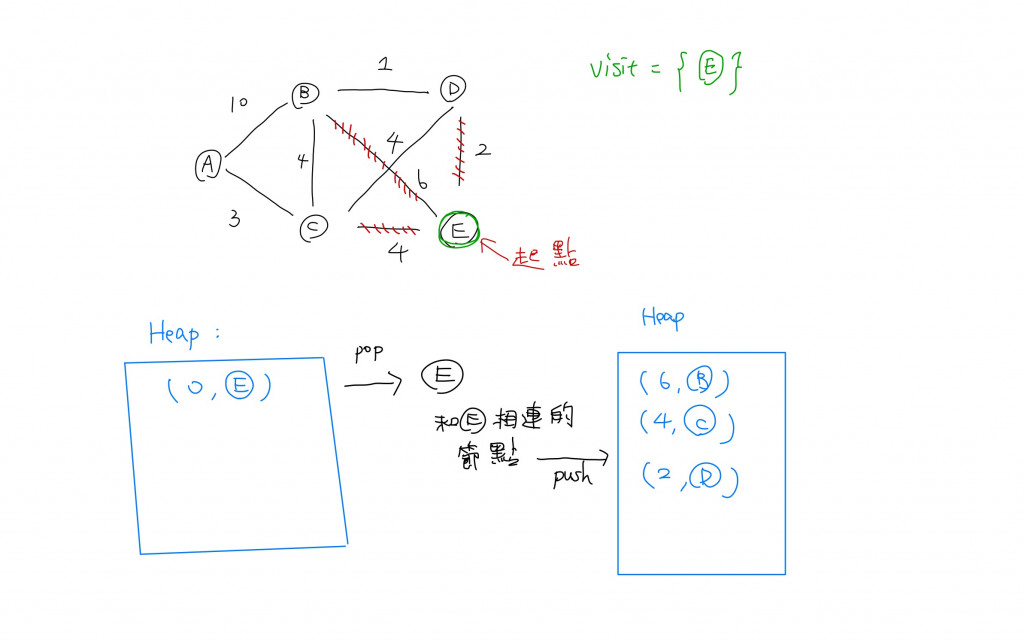
題目敘述：在二維平面上，給予一個包含了數個二維座標的array，當這些座標相連時我們以曼哈頓距離去定義他們之間的距離，找出他們之間最短的距離總和，並且每一個座標都要有辦法到達任一一個除了自己以外的座標。

Example: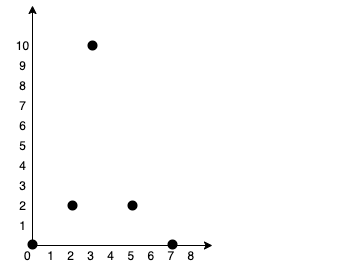

Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20

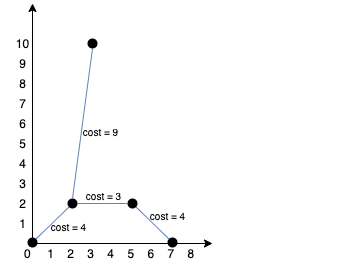
(圖源：leetcode)

分析：
這題正是要去求minimum spanning tree，我們首先需要將各座標和其餘的座標相連形成一張無向圖，並且利用adjacent list去保存。接著就可以利用heap和while迴圈來解題。我們每次都利用heap會優先找出在heap中距離最短的節點，並且去紀錄已經拜訪過這個節點了「這種greedy的策略」，下次再遇到這個節點時我們會忽略他，因為已經找到最佳的edge了。

class Solution:
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        adjList = defaultdict(list)
        for i in range(len(points)):
            for j in range(i + 1, len(points)):
                adjList[(points[i][0], points[i][1])].append((points[j][0], points[j][1]))
                adjList[(points[j][0], points[j][1])].append((points[i][0], points[i][1]))
        
        visit = set()
        h = [(0, points[0][0], points[0][1])]
        total = 0
        N = len(points)

        while len(visit) < N:
            cost, srcX, srcY = heapq.heappop(h)
            if (srcX, srcY) in visit:
                continue
            total += cost
            visit.add((srcX, srcY))

            for dstX, dstY in adjList[(srcX, srcY)]:
                if (dstX, dstY) not in visit:
                    dis = abs(dstX - srcX) + abs(dstY - srcY)
                    heapq.heappush(h, (dis, dstX, dstY))
        
        return total

希望在中秋節看到這篇而且正在準備面試的人都可以進到自己理想的公司XD