Hi 大家好，昨天稍微講解過用來代表Graph的資料結構後，今天要來解Graph中和Adjacency list相關的題目。

Leetcode 133. Clone Graph

題目敘述：有一Graph，並且我們定義了他的節點的資料結構：

class Node {
    public int val;
    public List<Node> neighbors;
}

每個節點都會有一個整數的值，並且以adjacency list去表示這個節點連像其他哪些節點。
現在題目要求要完全複製一個和這個Graph一樣的節點以及Edges。不可以在複製的Graph中使用原先的Graph中的節點。
input會是一個Node物件叫node代表了起點，之後我們也要return一個這個起點的複製（當然整個graph都要建立好）。

分析：我們可以使用DFS或BFS去拜訪原先的Graph中的每個節點，並且在初次拜訪這個節點時去創建新的Node物件，並且value和這個節點一樣。但是我們可能會在原Graph中拜訪到之前已經拜訪過的節點（像是A節點和B節點互相連向彼此，當我們初次拜訪A節點後，當我們拜訪B節點時B節點因為會連向A節點，所以我們又會再次拜訪到A節點），因此我們需要一個hashmap去儲存已經創建出克隆的節點，當我們又再次拜訪已經拜訪過的節點時，可以利用hashmap呼叫新創建的克隆節點，來建立這些克隆節點之間的edge。

BFS solution

"""Python
# Definition for a Node.
class Node:
    def __init__(self, val = 0, neighbors = None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []
"""

from typing import Optional
class Solution:
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        if not node:
            return node
        
        oldToNew = {}
        q = deque([node])
        oldToNew[node] = Node(node.val, [])

        while q:
            n = q.popleft()
            for neigh in n.neighbors:
                if neigh not in oldToNew:
                    oldToNew[neigh] = Node(neigh.val, [])
                    q.append(neigh)
                oldToNew[n].neighbors.append(oldToNew[neigh])
        
        return oldToNew[node]

DFS solution

"""
# Definition for a Node.
class Node:
    def __init__(self, val = 0, neighbors = None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []
"""

from typing import Optional
class Solution:
    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        oldToNew = {}

        def dfs(n):
            if n in oldToNew:
                return oldToNew[n]
            
            oldToNew[n] = Node(n.val)

            for neigh in n.neighbors:
                oldToNew[n].neighbors.append(dfs(neigh))
            
            return oldToNew[n]
        
        return dfs(node) if node else None

Leetcode 207. Course Schedule

敘述：給定好幾門課程，有些課程規定需要先修過其他課程才能來修（例如修過微積分才能修高等微積分），題目給予一個陣列，裡面有子陣列比如說[0,1]，代表要修過課程1才能修課程0。

Example1:

Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take. 
To take course 1 you should have finished course 0. So it is possible.

Example2:

Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take. 
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

分析：首先我們將圖利用Adjancency list建立出來。如果我們可以利用DFS去拜訪到所有的節點並且裡面沒有cycle的話就代表我們有辦法把這些課程都修完。

• 我們需要一個set是專門紀錄已經拜訪哪些節點了
• 我們還需要另外一個set是去紀錄在進行dfs當下走過的路徑是否會造成cycle

假設有一圖G1: 每次進行DFS時都會去紀錄下拜訪過哪些節點

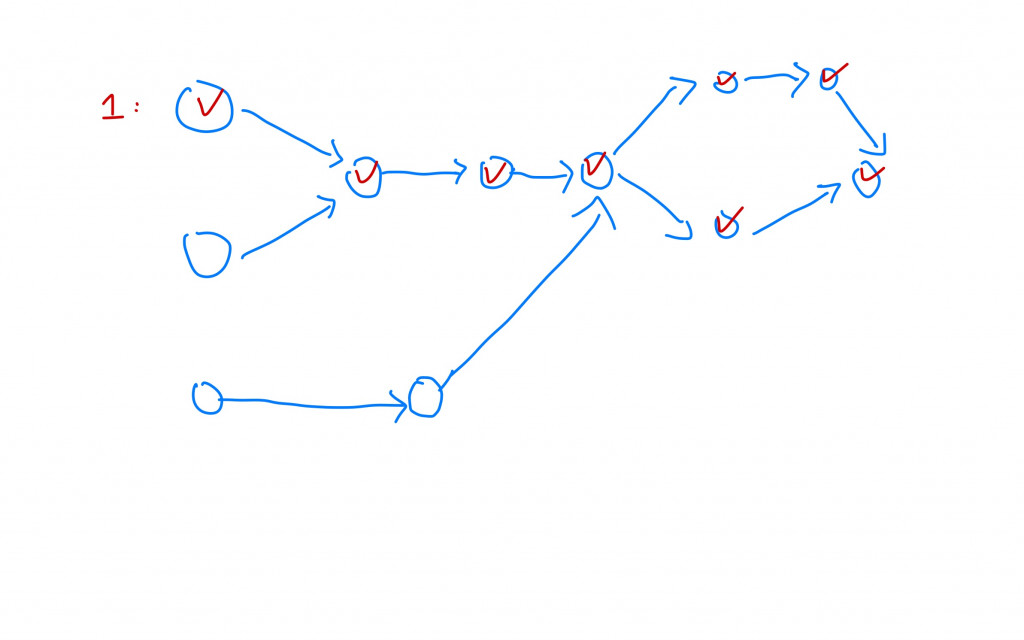
第二次從別的節點去進行拜訪：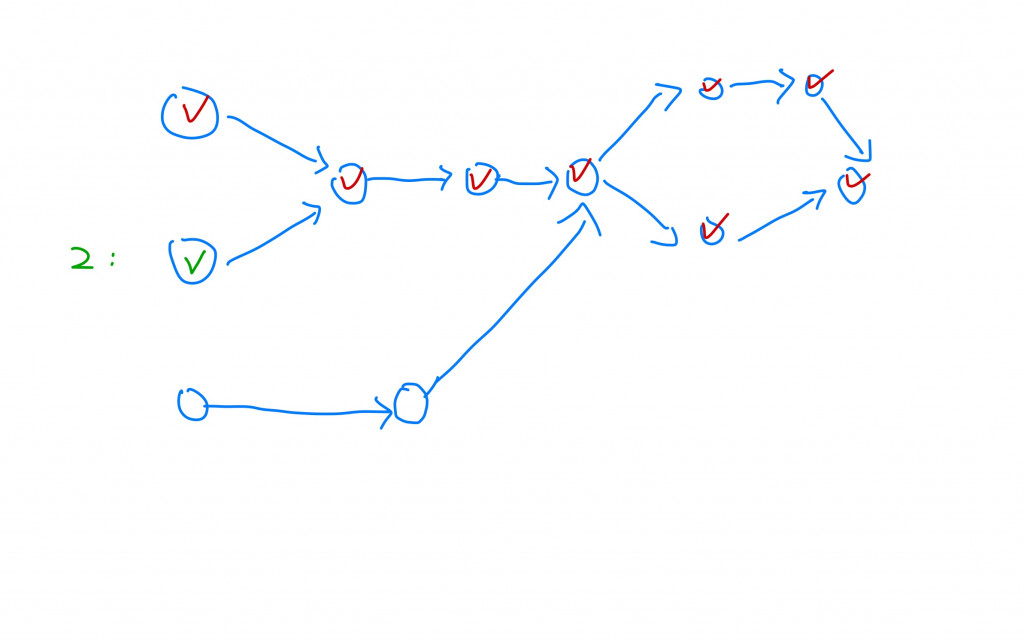

第三次從別的節點去拜訪，所有節點都可以拜訪，所以可以修完所有課程：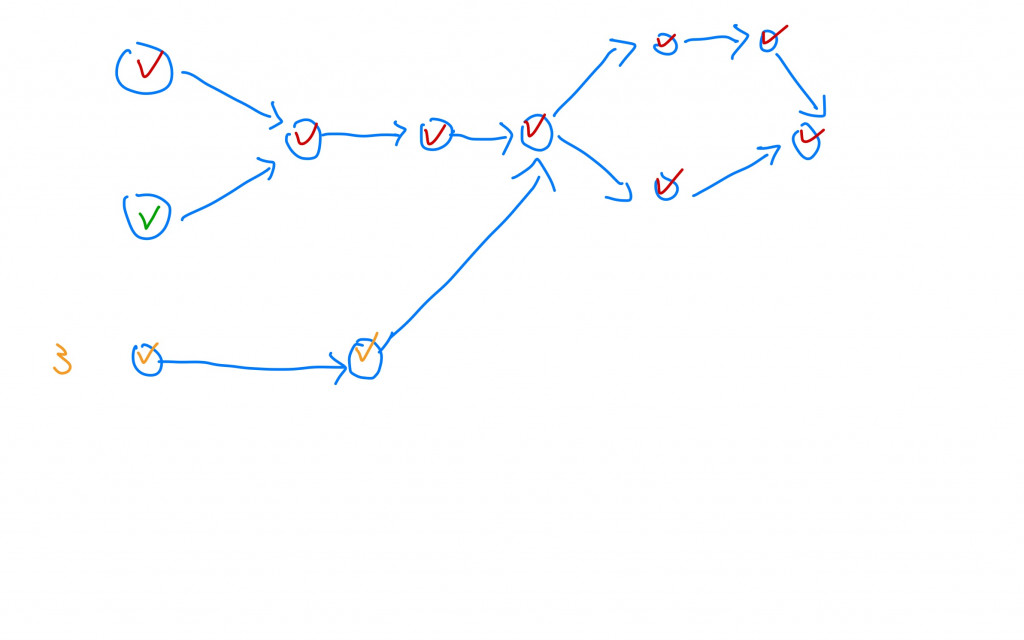

但是我們不只需要去紀錄拜訪過哪些節點，在進行DFS的時候也需要去檢查是否有迴圈，綠色的勾勾代表從某個節點開始一路的路徑：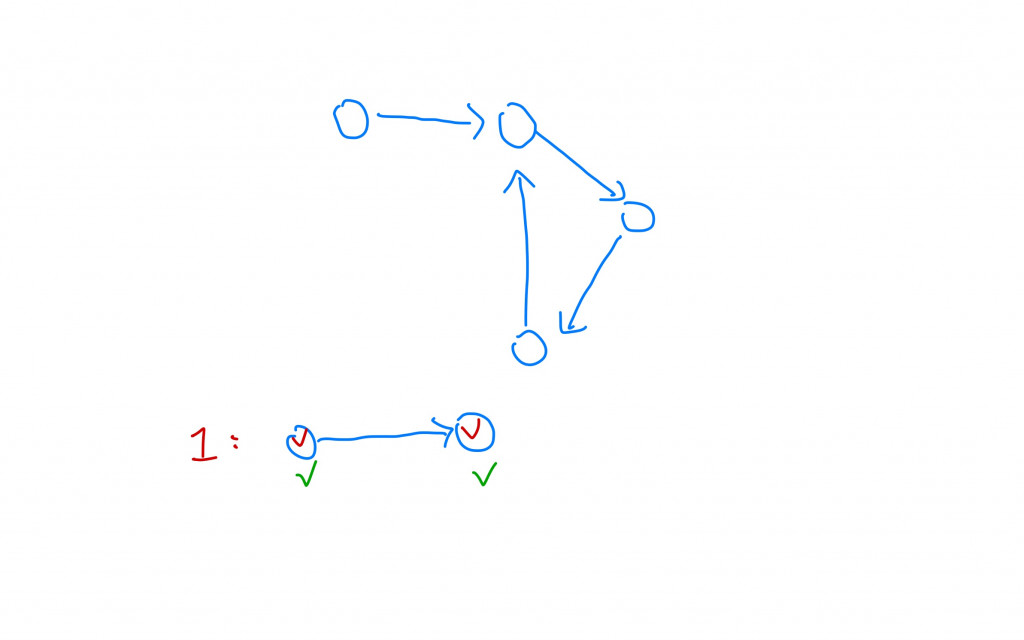

拜訪完那條路徑後，這些紀錄就會消失。而當在某條路徑上遇到已經拜訪過的節點代表有迴圈。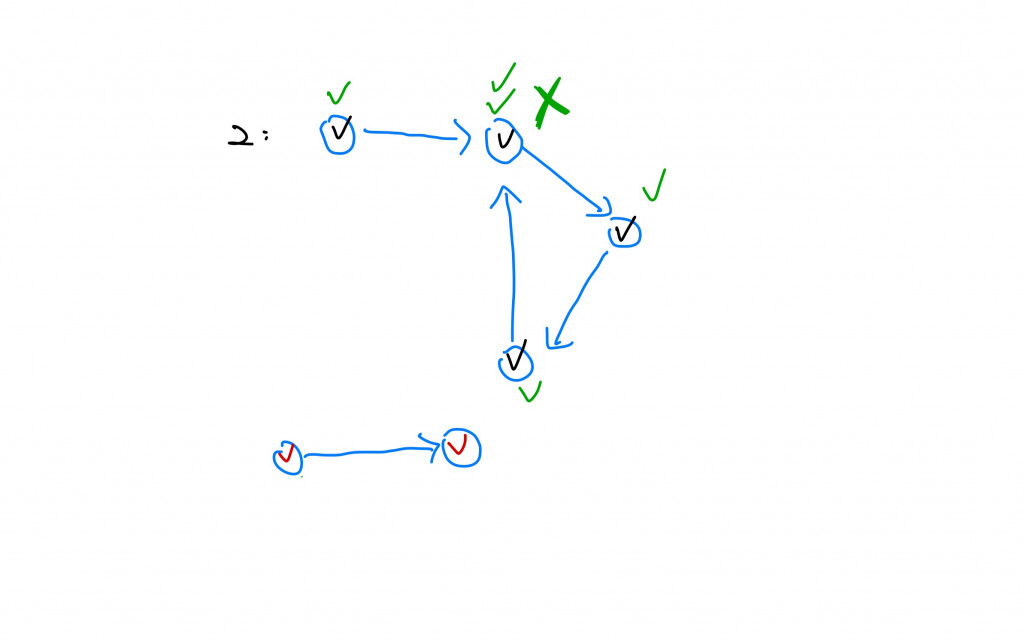

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        adjList = defaultdict(list)
        visit = set()
        for src, dst in prerequisites:
            adjList[src].append(dst)
        
        def dfs(node, cycle):
            if node in cycle:
                return False
            if node in visit:
                return True
            
            visit.add(node)
            cycle.add(node)
            for dst in adjList[node]:
                if not dfs(dst, cycle):
                    return False
            cycle.remove(node)
            return True

        for src in range(numCourses):
            if src not in visit:
                if not dfs(src, set()):
                    return False
        
        return True if len(visit) == numCourses else False

注意：在創建Adjacency list時，程式碼與敘述的source 和destination是相反的，不過沒差。

有時候坐在電腦前敲敲鍵盤在旁人眼中看起來好像是無所事事。但可能我們的腦中正在瘋狂激盪想辦法解決困難。只有自己知道這些努力的辛苦和他們能讓未來有所不同的價值。所以就相信自己吧。