於建立自變數(cause)和依變數(dependent variable)之間關係的統計模型
只有一個自變數和一個依變數之間的線性關係時
y=mx+b
有多個自變數和一個依變數之間的線性關係時
y=b0+b1x1+b2x2+…+bnxn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成隨機數據
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X + 1 + 0.1 * np.random.rand(100, 1)
# 創建線性回歸模型
model = LinearRegression()
model.fit(X, y)
# 進行預測
y_pred = model.predict(X)
# 繪製原始數據和回歸線
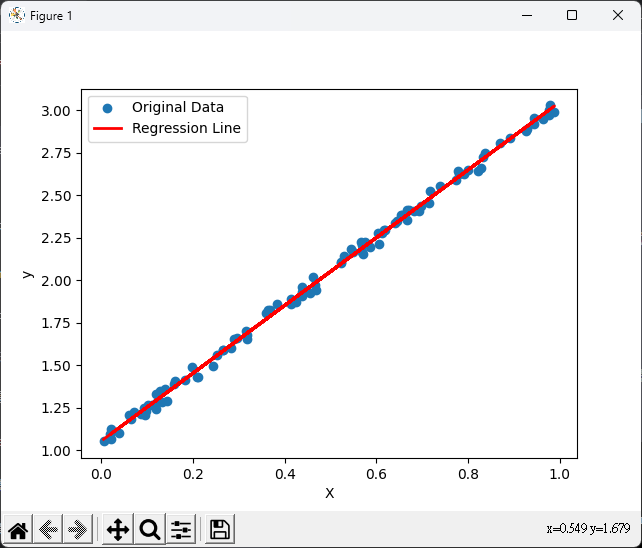
plt.scatter(X, y, label='Original Data')
plt.plot(X, y_pred, color='red', linewidth=2, label='Regression Line')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()
Kernal
from sklearn.svm import SVR
import matplotlib.pyplot as plt
from sklearn import datasets
# 生成一個具有200個樣本、1個特徵、1個目標變數和10的噪音水平的回歸dataset
X, y = datasets.make_regression(n_samples=200, n_features=1, n_targets=1, noise=10)
# 創建一個散點圖以視覺化生成的數據集
plt.scatter(X, y, linewidths=0.1)
# 創建支持向量回歸(SVR)模型的實例,使用linear核函數
model = SVR(kernel='linear', C=1.0)
model.fit(X, y)
# 使用模型對數據進行預測
predict = model.predict(X)
# 繪製回歸線
plt.plot(X, predict, c="red")
# 顯示原始數據的散點圖和預測的回歸線
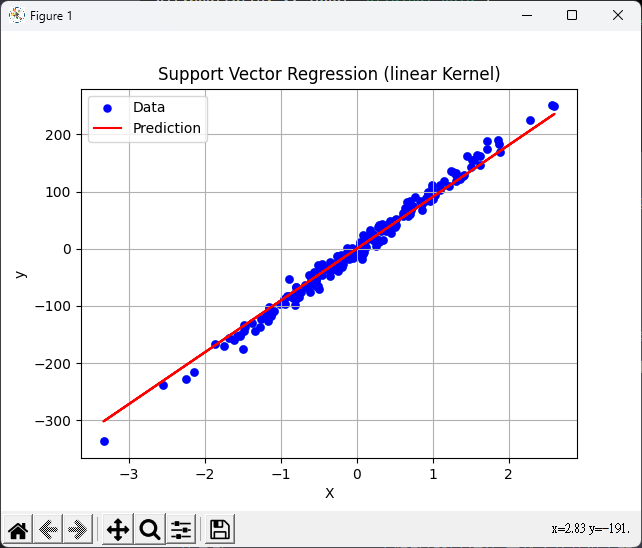
plt.scatter(X, y, linewidths=0.1, c='blue', label='Data')
plt.plot(X, predict, c='red', label='Prediction')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Support Vector Regression (linear Kernel)')
plt.grid(True)
plt.show()
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X + 1 + 0.1 * np.random.rand(100, 1)
# 創建多項式特徵
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)
# 使用線性回歸模型擬合多項式特徵
model = LinearRegression()
model.fit(X_poly, y)
# 預測
y_pred = model.predict(X_poly)
# 繪製原始數據和回歸線
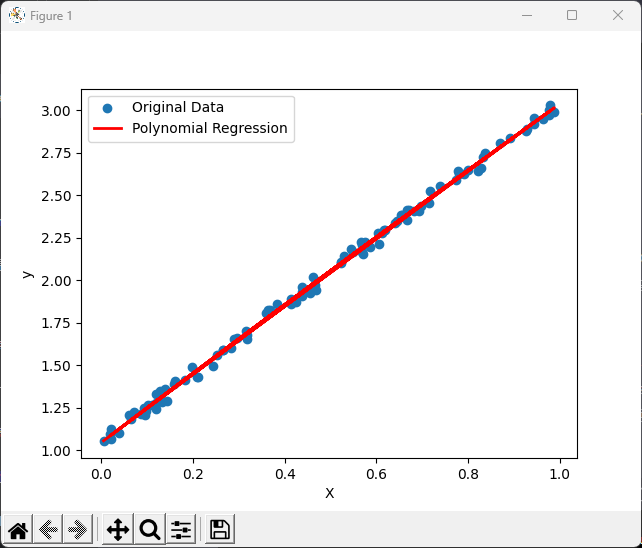
plt.scatter(X, y, label='Original Data')
plt.plot(X, y_pred, color='red', linewidth=2, label='Polynomial Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()
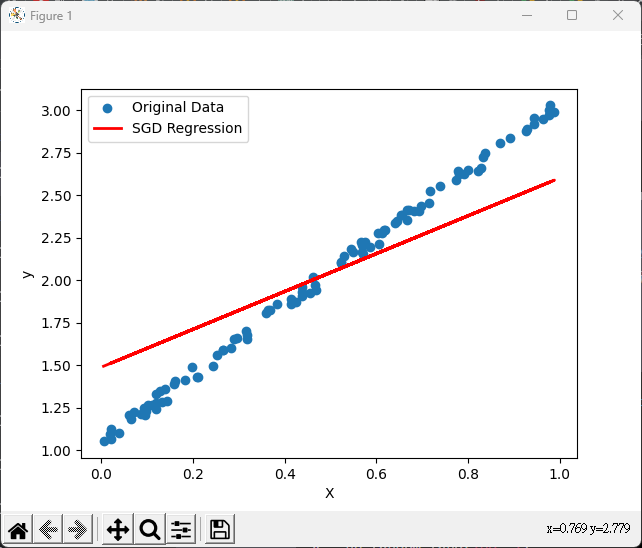
from sklearn.linear_model import SGDRegressor
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X + 1 + 0.1 * np.random.rand(100, 1)
# 創建隨機梯度下降回歸模型
model = SGDRegressor(max_iter=1000, eta0=0.01, random_state=0)
# 適配模型到數據
model.fit(X, y.ravel())
# 預測
y_pred = model.predict(X)
# 繪製原始數據和回歸線
plt.scatter(X, y, label='Original Data')
plt.plot(X, y_pred, color='red', linewidth=2, label='SGD Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()