前言:昨天帶大家看了權重初始化的標準常態分佈,今天會帶大家介紹Glorot分佈,明天會解決梯度不穩定的問題。
程式碼的部分中我們需要在匯入套件的地方就先import glorot_normal和glorot_uniform這兩個權重初始化器,我們新增在註解處那行
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense,Activation
from tensorflow.keras.models import Sequential
from tensorflow.keras import optimizers
from tensorflow.keras.utils import plot_model
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.initializers import Zeros,RandomNormal,glorot_normal,glorot_uniform #加入glorot_normal與glorot_uniform
import numpy as np
import matplotlib.pyplot as plt
接下來找到昨天設定權重初始值的地方,看大家要刪掉或是註解起來都可以,然後加入下面這一行,我們改用glorot常態分佈來設定權重初始值
w_init=glorot_normal()
我們可以看到跑出來的激活值分佈不那麼極端(畫出來的圖不一定會跟我的一樣,因為random()生成的亂數每次都不同)
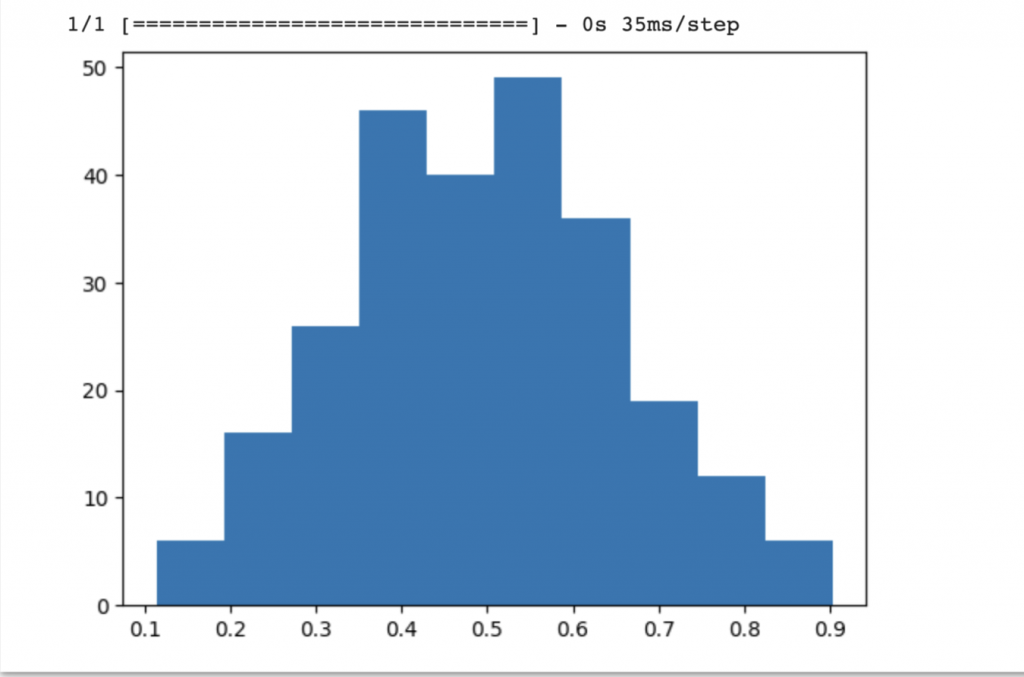
#完整程式碼
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense,Activation
from tensorflow.keras.models import Sequential
from tensorflow.keras import optimizers
from tensorflow.keras.utils import plot_model
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.initializers import Zeros,RandomNormal,glorot_normal,glorot_uniform
import numpy as np
import matplotlib.pyplot as plt
n_dense=256
n_input=784
b_init=Zeros()
w_init=glorot_normal()
model=Sequential()
model.add(Dense(n_dense,
input_shape=(784,),
kernel_initializer=w_init,
bias_initializer=b_init))
model.add(Activation('sigmoid'))
x=np.random.random((1,n_input))
a=model.predict(x)
_=plt.hist(np.transpose(a))
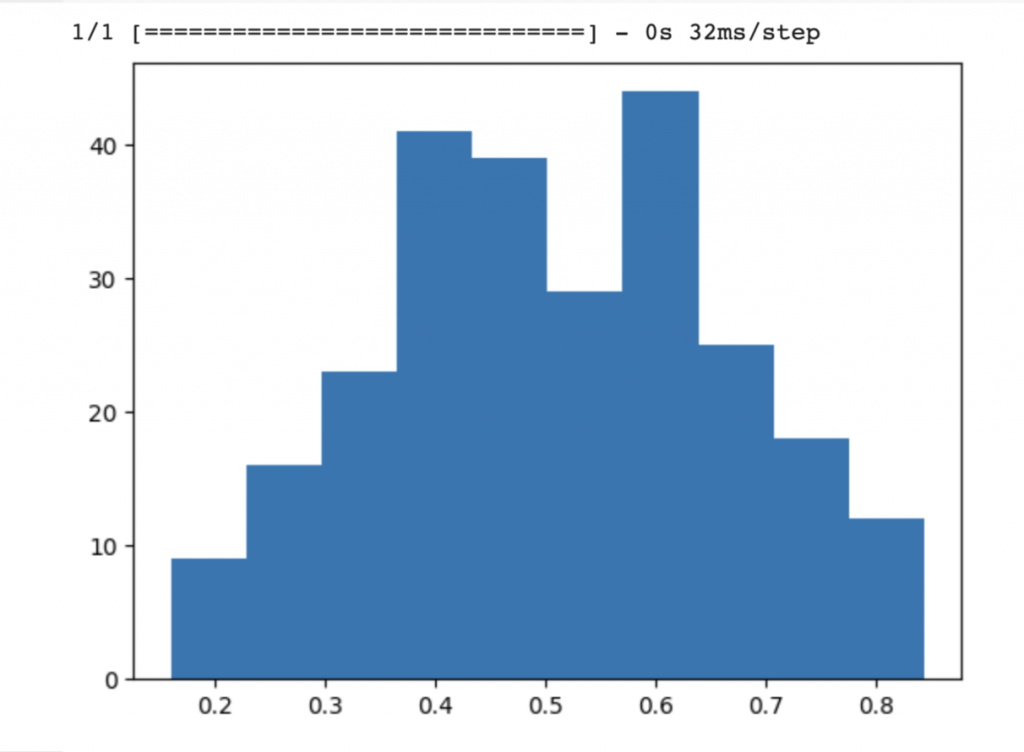
另外一個常用的是w_init=glorot_uniform(),我們改寫在14行,不過這與Glorot_normal常態分佈沒有什麼明顯差異,但我們還是來做做看
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense,Activation
from tensorflow.keras.models import Sequential
from tensorflow.keras import optimizers
from tensorflow.keras.utils import plot_model
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.initializers import Zeros,RandomNormal,glorot_normal,glorot_uniform
import numpy as np
import matplotlib.pyplot as plt
n_dense=256
n_input=784
b_init=Zeros()
w_init=glorot_uniform()
model=Sequential()
model.add(Dense(n_dense,
input_shape=(784,),
kernel_initializer=w_init,
bias_initializer=b_init))
model.add(Activation('sigmoid'))
x=np.random.random((1,n_input))
a=model.predict(x)
_=plt.hist(np.transpose(a))
第18天我們提到當神經元使用某些激活函數(如Sigmoid或Tanh)時,它們在輸入值較高或較低(極端值)的情況下容易飽和,所以我們來試試看換成激活函數Tanh來看看激活值分佈吧!我們先用標準常態分佈來看,要修改的地方後面都有加上註解
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense,Activation
from tensorflow.keras.models import Sequential
from tensorflow.keras import optimizers
from tensorflow.keras.utils import plot_model
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.initializers import Zeros,RandomNormal,glorot_normal,glorot_uniform
import numpy as np
import matplotlib.pyplot as plt
n_dense=256
n_input=784
b_init=Zeros()
w_init=RandomNormal(stddev=1.0) #標準常態分佈
model=Sequential()
model.add(Dense(n_dense,
input_shape=(784,),
kernel_initializer=w_init,
bias_initializer=b_init))
model.add(Activation('tanh')) #激活函數tanh
x=np.random.random((1,n_input))
a=model.predict(x)
_=plt.hist(np.transpose(a))
tanh搭配標準常態分佈初始化權重,可以發現產生的激活值也比較極端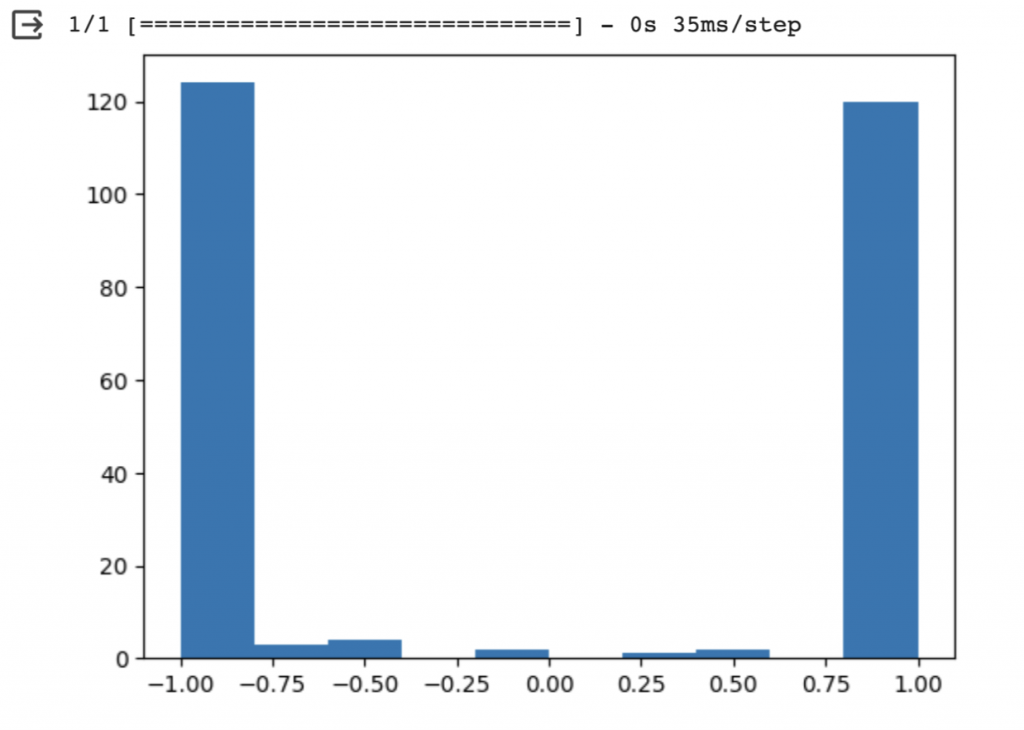
我們把程式碼第14行改成w_init=glorot_normal #glorot常態分佈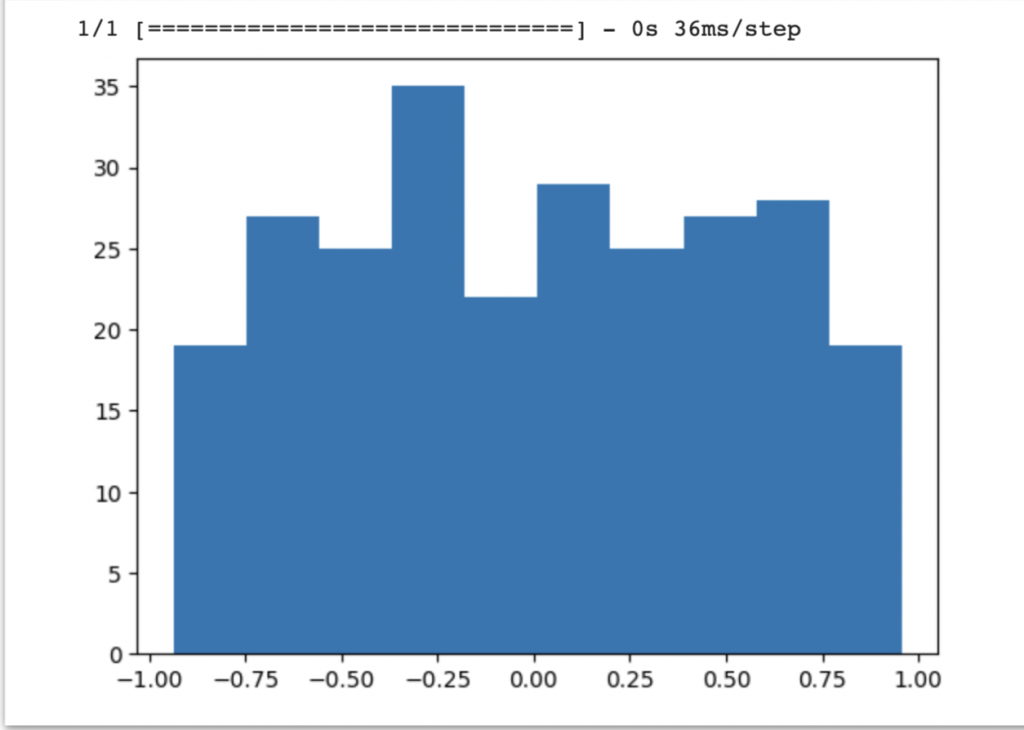
總結:綜合以上結果,我們可以發現用glorot分佈下激活值分佈的平均且沒有極端值的出現,這樣有助於確保模型在訓練過程中更穩定地收斂,並且減少梯度消失或梯度爆炸的問題。而glorot分佈應該也是設定權重初始化目前最流行的用法之一
