John C lauser、Michael Horne、Abner Shemony和 Richard Holt導出了CHSH 不等式，可用來證明貝爾定理：
𝑆= 𝑍𝑊+ 𝑋𝑊− 𝑋𝑉+ 𝑍𝑉
而𝑍𝑊+ 𝑋𝑊− 𝑋𝑉+ 𝑍𝑉= ( 𝑍+ 𝑋) 𝑊+ ( 𝑍− 𝑋) 𝑉

根據之前的Bell實驗修改
假設Espian 將創建一對 EPR，並將一個量子位元傳送給 Asja，將第二個量子位元傳送給 Balvis。
Asja 在兩個偵測器之間進行選擇並執行測量：Z或者X
Balvis 在兩個偵測器之間進行選擇並執行測量：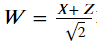
或者
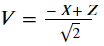
為簡單起見，我們假設每個測量都可以有兩個結果之一+1或者−1

因為測量結果可以是 +1或者−1
(𝑍+𝑋)𝑊=0
(𝑍−𝑋)𝑉=±2
(𝑍−𝑋)𝑉=0
(𝑍+𝑋)𝑊=±2
所以S=±2

Quantum correlation

假設初始狀態是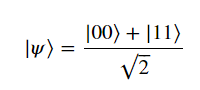
而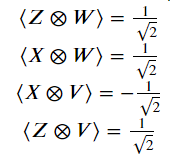
因此CHSH的計算結果S=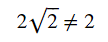

違反 CHSH 不等式可作為量子糾纏的指標！

實驗

讓我們執行四個實驗，每個實驗 100 次並收集統計數據。

1st experiment - ⟨𝑍⊗𝑊⟩:

從 EPR 對開始，Asja 將測量第一個量子位元 (qreg[0])，Balvis 將測量第二個量子位元 (qreg[1])。
Asja 在 𝑍-base實施上，Balvis在 𝑊-base。
將測量base旋轉至 𝑊-axis，使用門序列： 𝑆-𝐻−𝑇-𝐻

2nd experiment - ⟨𝑋⊗𝑊⟩:

從 EPR 對開始，Asja 將測量第一個量子位元 (qreg[0])，Balvis 將測量第二個量子位元 (qreg[1])。
Asja 在 X-base實施上，Balvis在 𝑊-base。

3rd experiment - ⟨𝑋⊗𝑉⟩:

從 EPR 對開始，Asja 將測量第一個量子位元 (qreg[0])，Balvis 將測量第二個量子位元 (qreg[1])。
Asja 在 X-base實施上，Balvis在 V-base。
將測量base旋轉至 V-axis，使用門序列：𝑆-𝐻−T†–𝐻

4th experiment - ⟨𝑍⊗𝑉⟩:

從 EPR 對開始，Asja 將測量第一個量子位元 (qreg[0])，Balvis 將測量第二個量子位元 (qreg[1])。
Asja 在 𝑍-base實施上，Balvis在 V-base。

# import all necessary objects and methods for quantum circuits
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer
from random import randrange

ZW

#1st experiment - ZW
qreg = QuantumRegister(2)
creg = ClassicalRegister(2) 
mycircuit1 = QuantumCircuit(qreg, creg)

#Creating entanglement
mycircuit1.h(qreg[0])
mycircuit1.cx(qreg[0], qreg[1])

#Asja measure 1st qubit qreg[0] in Z basis, thus do nothing

#Balvis measure 2nd qubit qreg[1] in W basis, thus applies S-H-T-H gates first
mycircuit1.s(qreg[1])
mycircuit1.h(qreg[1])
mycircuit1.t(qreg[1])
mycircuit1.h(qreg[1])

mycircuit1.draw(output='mpl')

mycircuit1.measure(qreg,creg)

job = execute(mycircuit1,Aer.get_backend('qasm_simulator'),shots=100)
countsZW = job.result().get_counts(mycircuit1)
print(countsZW) # counts is a dictionary

{'00': 39, '11': 44, '10': 4, '01': 13}

XW

#2nd experiment - XW
qreg = QuantumRegister(2)
creg = ClassicalRegister(2) 
mycircuit2 = QuantumCircuit(qreg, creg)

#Creating entanglement
mycircuit2.h(qreg[0])
mycircuit2.cx(qreg[0], qreg[1])

#Asja measure 1st qubit qreg[0] in X basis
mycircuit2.h(qreg[0])

#Balvis measure 2nd qubit qreg[1] in W basis
mycircuit2.s(qreg[1])
mycircuit2.h(qreg[1])
mycircuit2.t(qreg[1])
mycircuit2.h(qreg[1])

mycircuit2.draw(output='mpl')

mycircuit2.measure(qreg,creg)

job = execute(mycircuit2,Aer.get_backend('qasm_simulator'),shots=100)
countsXW = job.result().get_counts(mycircuit2)
print(countsXW) # counts is a dictionary

{'11': 43, '10': 9, '00': 45, '01': 3}

XV

#3rd experiment - XV
qreg = QuantumRegister(2)
creg = ClassicalRegister(2) 
mycircuit3 = QuantumCircuit(qreg, creg)

#Creating entanglement
mycircuit3.h(qreg[0])
mycircuit3.cx(qreg[0], qreg[1])

#Asja measure 1st qubit qreg[0] in X basis
mycircuit3.h(qreg[0])

#Balvis measure 2nd qubit qreg[1] in V basis
mycircuit3.s(qreg[1])
mycircuit3.h(qreg[1])
mycircuit3.tdg(qreg[1])
mycircuit3.h(qreg[1])

mycircuit3.draw(output='mpl')

mycircuit3.measure(qreg,creg)

job = execute(mycircuit3,Aer.get_backend('qasm_simulator'),shots=100)
countsXV = job.result().get_counts(mycircuit3)
print(countsXV) # counts is a dictionary

{'10': 41, '01': 40, '11': 11, '00': 8}

ZV

#3rd experiment - ZV
qreg = QuantumRegister(2)
creg = ClassicalRegister(2) 
mycircuit4 = QuantumCircuit(qreg, creg)

#Creating entanglement
mycircuit4.h(qreg[0])
mycircuit4.cx(qreg[0], qreg[1])

#Asja measure 1st qubit qreg[0] in Z basis

#Balvis measure 2nd qubit qreg[1] in V basis
mycircuit4.s(qreg[1])
mycircuit4.h(qreg[1])
mycircuit4.tdg(qreg[1])
mycircuit4.h(qreg[1])

mycircuit4.draw(output='mpl')

mycircuit4.measure(qreg,creg)

job = execute(mycircuit4,Aer.get_backend('qasm_simulator'),shots=100)
countsZV = job.result().get_counts(mycircuit4)
print(countsZV) # counts is a dictionary

{'00': 45, '01': 13, '10': 6, '11': 36}

計算CHSH

ZW=(countsZW.get('00')+countsZW.get('11')-countsZW.get('01')-countsZW.get('10'))/100
XW=(countsXW.get('00')+countsXW.get('11')-countsXW.get('01')-countsXW.get('10'))/100
XV=(countsXV.get('00')+countsXV.get('11')-countsXV.get('01')-countsXV.get('10'))/100
ZV=(countsZV.get('00')+countsZV.get('11')-countsZV.get('01')-countsZV.get('10'))/100

print(ZW, XW, XV, ZV)

S=ZW+XW-XV+ZV

print("CHSH inequality value is", S)

CHSH inequality value is 2.66

也就是說

而這樣的特性可以用作量子糾纏的指標
因此可以應用在E91 Protocal 中

參考資料:Womanium教材