今天要來談跟演算法息息相關的樹狀結構 🌳

▌樹狀結構

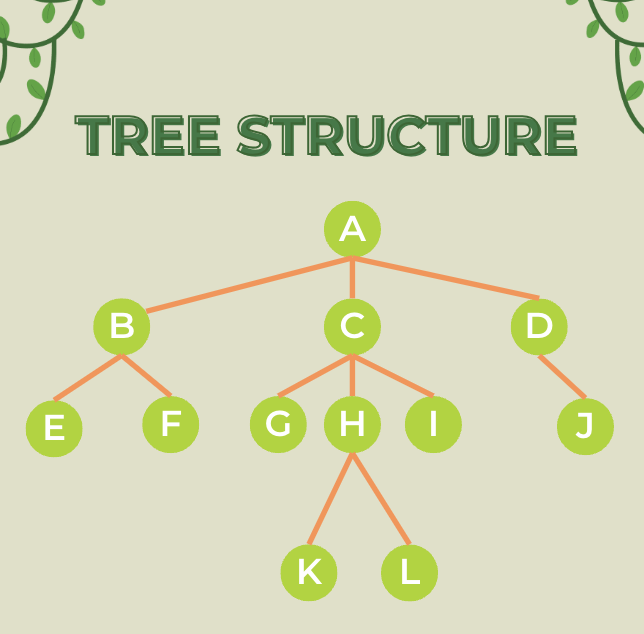
樹（tree）在電腦的世界中是一個很重要的概念！由節點（Node）和邊（edge）所構成「樹狀結構」，是一種抽象的資料結構

節點可以細分為以下三種：

• 根節點（Root Node）
  最上層開始的節點，由根節點開始長出其他子節點，如同樹木的根。例如上圖中的 A 就是根節點

• 外部節點（Internal Node）
  又稱作「葉節點 leaf node」，位於樹的最下層。例如上圖中的 E、F、G、K、L、I、J 節點

• 內部節點（External Node）
  「外部節點」和「根節點」以外的所有節點都屬於內部節點。例如上圖中的 B、C、D 等

▪ 特點以及常見專有名詞

特點：

• 只有一個根節點（Root Node）
• 沒有迴圈（loop）
  也就是任何一個節點只能依照邊往下走，不能再走回去找自己
• 點跟點之間只有唯一的路徑
  例如上圖中的 G 節點要走到 A 節點的話，一定會經過 C 節點，沒有其他走法了，可以說只有唯一的路徑，且是固定的

常見專有名詞：

▪ 高度（Height）

樹的高度 ＝ 從「根節點」到「外部節點」的途中，總共經過的節點（取最多的那個）

例如上圖中最遠的外部節點是 K 或 L ，他們距離 A 根節點共有 4 個節點（K、H、C、A），外部節點自己也要算進去，所以也可以說這棵樹的高度是 4

▪ 階層（Level）

樹的階層 ＝ 任何一個節點和根節點間的距離

以上圖為例，列出各個階層有哪些節點

▪ 祖先節點（Ancestor Node）

我們知道點跟點之間只有唯一的路徑。那從某個節點向上延伸的這個唯一路徑中所遇到的節點，都是某個節點的「祖先節點」。舉例應該比較好懂，上圖中以 K 節點來說，它的「祖先節點」有 H、C、A

▪ 父節點（Parent Node）

「祖先節點」裡也包含「父節點」，也就是最靠近目前節點的「祖先節點」（好繞口XD
以上圖中的 K 節點來說，它的「父節點」是 H

▪ 子孫節點（Descendant Node）

就是某個節點的下面所有節點，包括他的孩子、孫子、曾孫
以上圖中的 C 節點來說，它的「子孫節點」有 G、H、I、K、L

▪ 子節點（Child Node）

「子孫節點」裡也包含「子節點」，是最靠近某個節點的「子孫節點」。跟上面「父節點」和「祖先節點」的關係差不多。以上圖中的 C 節點來說，第一層 G、H、I 就都是它的「子節點」

▌二元樹（Binary Tree）

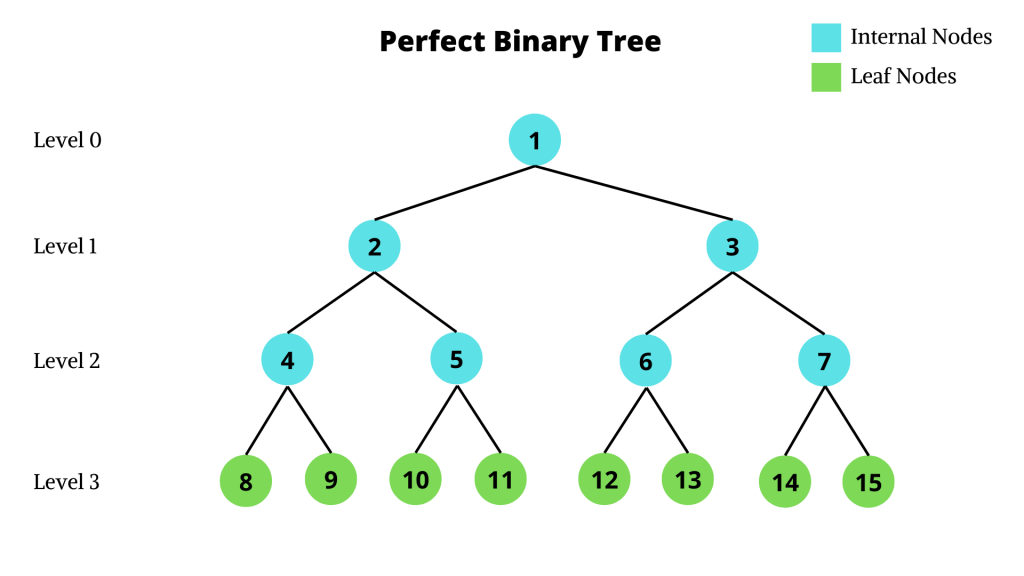
Perfect Binary Tree 圖片來源

每一個節點「最多」只有兩個子節點！所以也有可能只有「一個」或是「無子節點」

針對二元樹的每一個節點，都有其資料型態，可不必相同！不過要注意，若只有一個子節點或沒有子節點的話，就定義為 null

▪ 幾種特殊類型的二元樹

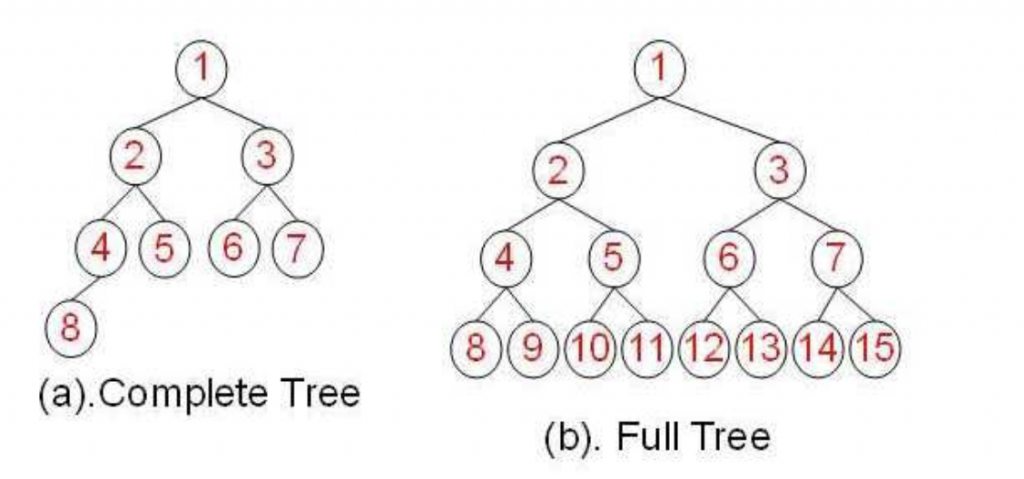
圖片取自wiki
Perfect Binary Tree 示意圖可以參考上上張圖

• Full Binary Tree：除了 leaf node （葉節點/外部節點）以外，每個節點都有兩個子節點
• Complete Binary Tree：除了最後一層，其他層的節點都是全滿，且最後一層節點會全部靠左
• Perfect Binary Tree： 同時也是 full binary tree 和 complete binary tree ，所有「非外部節點」都有兩個子節點，而且所有階層的節點必須是全滿的

▪ 二元樹也有左邊、右邊？

左子樹與右子樹 （圖片來源）

• 「左子節點」（Left Child Node）：位於「左邊」的節點。若以左子節點中最上頭的節點為根節點，那麼組成的樹叫做「左子樹」（Left Subtree）
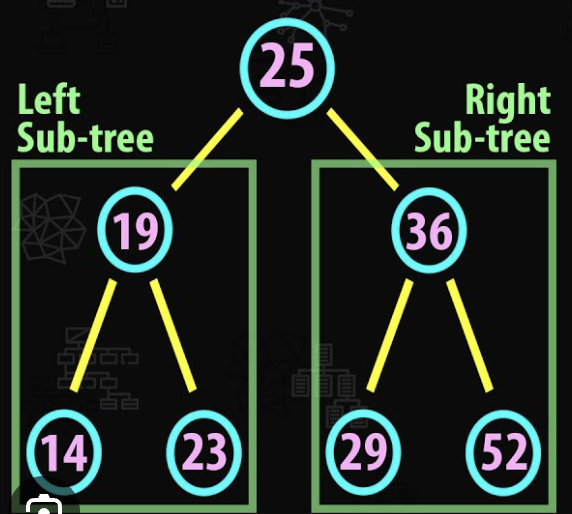
• 「右子節點」（Right Child Node）：位於「右邊」的節點。對應的樹叫做「右子樹」（Right Subtree）

圖片來源

上圖這個二元樹也稱作「運算樹」（Expression Tree），其中運算子（Operator）是「父節點」，運算元（Operand）為「子節點」。運算的結果為 (5 * 4) + (100 - 20) = 100

▪ 如何訪問/遍歷（treverse）二元樹中的所有節點

有以下三種訪問方式：

• 前序法（Pre Order）：父節點 ➡ 左子節點 ➡ 右子節點
  以上面「運算樹」為例會得到 +*54-10020。「前序法」的概念可以對應到 DFS（Depth-First-Search, 深度優先搜尋演算法），先往第一個節點的最深處走，再去找其相鄰的點，如果當前的節點已經訪問過，那就則回到上一個點(backtracking)，繼續找其他還沒走訪過的點

• 中序法（In Order）：左子節點 ➡ 父節點 ➡ 右子節點
  以上面「運算樹」為例會得到 5*4+100-20

• 後序法（Post Order）：左子節點 ➡ 右子節點 ➡ 父節點
  以上面「運算樹」為例會得到 54*10020*+

• 層序法（Level Order）：「由上到下」一層層走訪，並在同個階層中「由左至右」依序訪問，直到所有的節點都走完！這樣的搜方式可以對應到 BFS（Breadth-First Search, 廣度優先搜尋演算法）。 以上面「運算樹」為例會得到 +*-54100/202

這三種訪問方式，可用「父節點」訪問的順序來做簡單的判斷，前序法父節點會放在最前面，中序法就是中間。此外都有應用「遞迴」（recursive）的觀念，就是在程序的本體中又呼叫到自己，較常用於描述以相似方法重複事物的過程，像是階層函數（Factorial Function）（好像回到高中數學XD）

0!=1
n!= (n-1)! * n

剛好看到有一篇文章在講遞迴的思考方式，覺得寫得蠻淺顯易懂的！分享給大家 點我

附上幾個 Leetcode 的 binary tree 的題目

1. Binary Tree Preorder Traversal
2. Binary Tree Inorder Traversal
3. Binary Tree Postorder Traversal

▌總結

雖然樹狀結構是抽象的資料結構，但其實概念跟人類的族譜、血緣蠻相近的。在樹的演算法中，常使用到「遞迴」（recursive）的概念，DFS（深度優先搜尋） 演算法也是其經典的應用。另外，同棵樹中的節點都有相同的特性，前面的處理結果會影響到後面的，我們也可以把二元樹的結構看成是比較複雜的「鏈接串列」

▌參考資料

1. wikipedia
2. Tree 樹狀資料結構
3. 台灣師範大學 Binary Tree