依稀記得小時候曾跟家人去老爺酒店，當時看到酒店的櫃檯有一本很厚的電話查找簿🤣，假設今天要找某個字母開頭的公司，可以從第一頁開始翻，也可以從尾巴開始找，但我們其實也可以透過二元搜尋法來處理喔

▌二元搜尋法（Binary Search）

「二元搜尋法」又叫「折半搜尋法」、「對數搜尋法」。是一種在排序數組或列表中查找特定元素的演算法，特點是每次比較後都會把剩餘的元素二等分，可以大幅度提高搜索速度。但要特別注意，被搜尋的數列必須要是有經過排序的，如果要找的元素存在的話，就會還傳該元素的位置編號，如果不存在就會回傳 null

▪ 畫成圖如下：

▪ 拆解成步驟如下：

1. 初始化：選取數組的中間元素
2. 比較：將中間元素與目標值進行比較
3. 調整搜尋範圍：
   若中間元素 = 目標值 => 搜索成功
   若目標值 < 中間元素 => 則在數組的左半部分繼續搜索
   若目標值 > 中間元素 => 則在數組的右半部分繼續搜索
4. 重複：返回步驟1，直到找到目標元素或搜索範圍為空

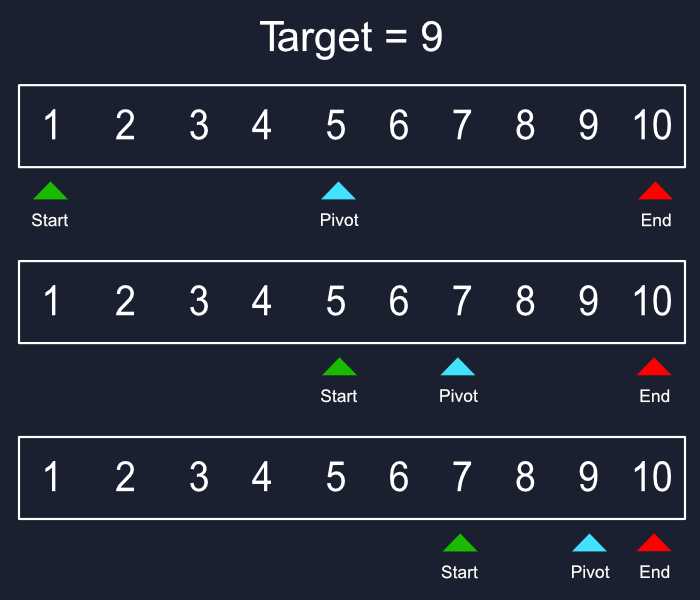
附上 JS 實現「二元搜尋法」的範例程式。「二元搜尋法」的「時間複雜度」是 O(log n)，這個複雜度代表每次搜索都會將問題的規模減少為原來的一半。
如果對 Big O Notation 不是很了解，可參考昨天寫的這篇文章開頭部分

function binarySearch(arr, target) {
  let low = 0;
  let high = arr.length - 1;

  // 調整搜尋範圍
  while (low <= high) {
    const mid = Math.floor((low + high) / 2);

    if (arr[mid] === target) {
      return mid;
    }

    if (arr[mid] < target) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }

  return -1;
}

// 測試
const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]; // 已排列數組
const target = 7; // 目標值

const resultIdx = binarySearch(sortedArray, target);
if (resultIdx !== -1) {
  console.log(`找到目標 ${target} 在索引 ${resultIdx}`);
} else {
  console.log(`未找到目標 ${target}`);
}

▌總結

二元搜尋法是個簡單又快速的搜尋演算法，特別適用於大型的資料集合，相較於線性搜索（每次只能減少一個元素），二元搜尋法在大型資料集上的效率更好。不過它也有侷限性，像是會需要一個已排序的數組來進行搜索，這點須特別留意

▌參考資料

1. wikipedia
2. 計算機概論 全華
3. 白話演算法 旗標出版