• 課程網址 https://course.fast.ai/Lessons/part2.html
• 上課影片
• notebook

調度器（Scheduler）

在整個穩定擴散過程中，我們不是一次性地去除所有的噪點，而是透過多次迭代逐步減少噪點。這種逐步的方法提供了更好的控制和更精細的生成結果。但問題來了：我們應該在每一步添加多少噪點？這些噪音應該如何隨時間變化？這就是為什麼我們需要一個調度器（Scheduler）的原因。

調度器的主要職責是在整個擴散過程中確定每一步的噪點量。它根據預先定義的策略和參數（如起始和結束的噪音量、噪音變化的策略等）來做這個決定。

set_timesteps是用來設定在生成過程中進行的"去噪"步驟數量，我們先告訴調度器我們想要在15步內完成整個擴散去噪過程。

set_timesteps(scheduler, 15)

那為什麼是設15呢?
控制生成時間：擴散去噪的步驟數量直接影響生成圖像所需的時間。數字設更大可能會生成更高的圖像質量，但也需要更長的時間。
通常在使用這種模型時，我們可能會進行多次實驗，使用不同的步驟數量來看哪一個設定能得到最佳結果。

我們可以從下面的指令來觀察他的調度結果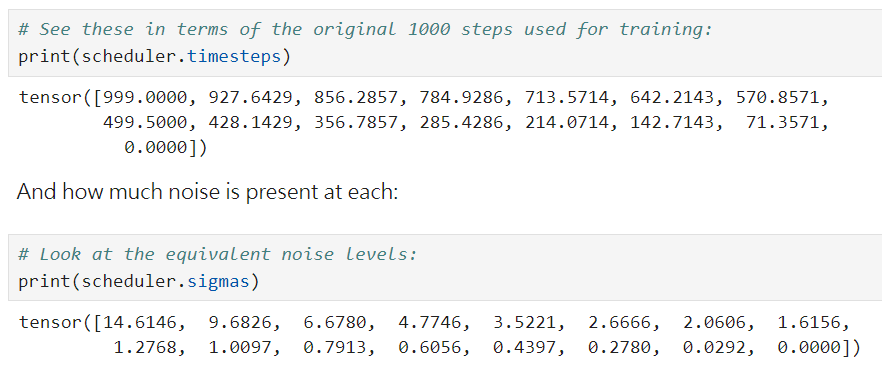

可以看到在timesteps 時，一開始用較大的步長(超過70)，後面慢慢減少。
而在印出sigma(每一步的雜訊標準差，或說雜訊強度)時，可以看到：

• 遞減的雜訊強度：這些值開始於一個相對較高的雜訊標準差，然後逐步減少。表示在擴散過程的開始，模型面對的是較強的雜訊，隨著過程進行這些雜訊逐漸減少。

• 開始和結束的極端值：在這組值中，最初的數字（例如 14.6146）表示開始時的高雜訊強度，而接近 0 的值（例如 0.0292 和 0.0000）表示過程的結束，這時雜訊強度非常低。

• 遞減速率：可以注意到這些值的遞減速率並不是均勻的。在開始時遞減得較快，而接近結束時，減少的速度則放緩。

這些遞減的雜訊強度值是經過策略性選擇的，目的是在擴散過程中逐步引導模型從噪音圖像恢復到原始或目標圖像。這也解釋了為什麼在擴散的開始，模型會面對更大的挑戰（即更高的噪音強度），而隨著步驟的進行，這些挑戰逐漸減少。
我們可以做視覺化來觀察雜訊的變化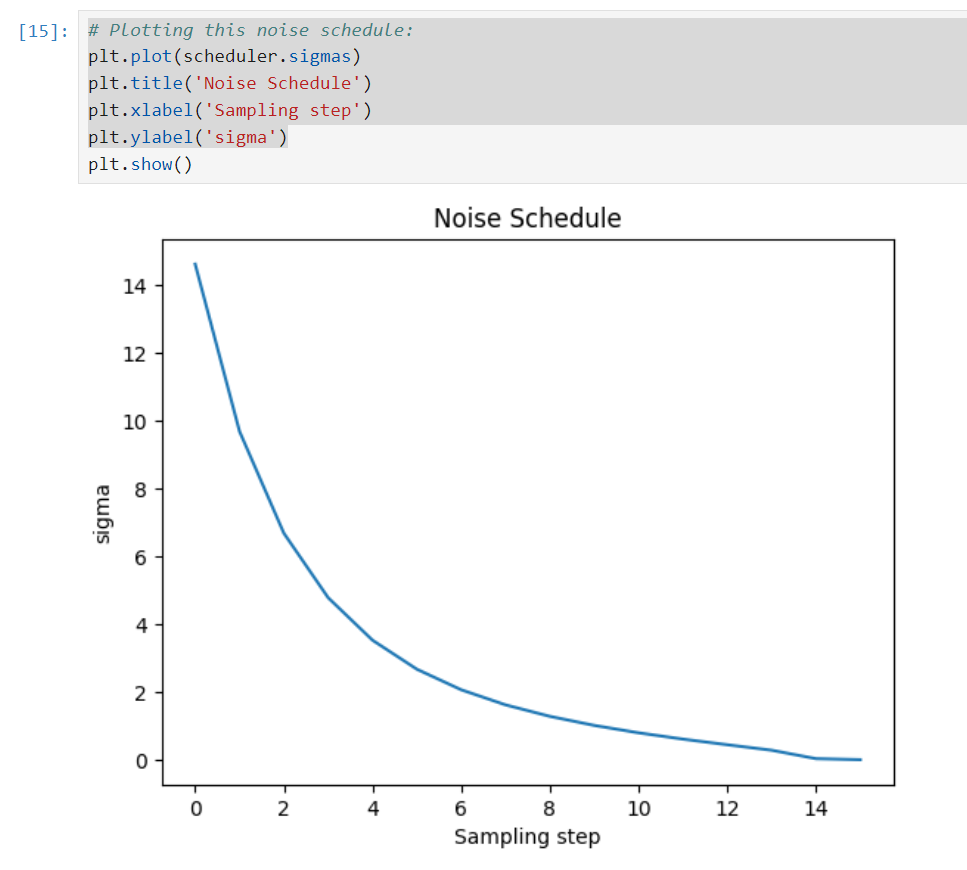

加入雜訊後，解碼回圖像

以下我們想要視覺化「雜訊」在潛在空間中的影響。也就是說我們想要查看當我們在潛在表示中加入noise後，解碼回圖像空間的結果會是什麼。

1. 生成隨機雜訊

noise = torch.randn_like(encoded) # Random noise

2. 選擇一個采樣步驟：

sampling_step = 10 # Equivalent to step 10 out of 15 in the schedule 

這邊選擇了第10步作為采樣步驟。表示將使用與上述15步中的第10步相對應的雜訊強度。

3. 將噪音添加到已編碼的圖像：

encoded_and_noised = scheduler.add_noise(encoded, noise, timesteps=torch.tensor([scheduler.timesteps[sampling_step]]))

使用 scheduler.add_noise 函數來添加雜訊。我們將先前生成的隨機噪音和第10步的雜訊強度（從 scheduler.timesteps 獲得）添加到已編碼的圖像 encoded。

4. 解碼噪音後的潛在表示：

latents_to_pil(encoded_and_noised.float())[0] # Display

最後，我們使用 latents_to_pil 函數將加入噪音的潛在表示解碼回圖像空間並顯示結果。

透過這段程式，我們可以看到添加噪音後的潛在表示如何影響圖像的最終外觀。幫助我們理解噪音在整個擴散過程中的角色，以及它是如何與原始內容互動的

最後講師給了一些建議，對象是於那些想要深入研究或自行調整模型的使用者。知道模型的內部運作可以幫助他們作出明智的決策並優化結果。

• 不同的噪音和調度方法：

有些擴散模型在不同的雜訊水平下保持變異性相對恆定，這被稱為「variance preserving」。
其他模型則隨著增加的雜訊，變異性逐漸增加，這被稱為「variance exploding」。

• 從隨機噪音開始：

如果我們想從隨機噪音而不是雜訊圖像開始，我們需要根據訓練期間使用的最大sigma值對其進行縮放。在這種情況下，該值大約是14。

• 預調節步驟：

在將這些雜訊潛變量提供給模型之前，它們會在所謂的預調節步驟中進一步縮放。
這個縮放過程確保了模型能夠更好地處理這些雜訊潛變量，並使其更容易進行後續的「去噪」過程。