零、前言

在上一篇中講到 Model 形成的概念，便是透過模擬人類神經元的 Perceptron感應器而初步建立的 Layers 組合就成為 Model，我們也在過程中得知機器學習的過程就是在訓練這些參數。那不免讓我們好奇的是，這些變數如 weight、bias…等，要使電腦透過何種機制來評估何以使預測的準確度提升呢？

一、損失與損失函數

準確度與誤差問題

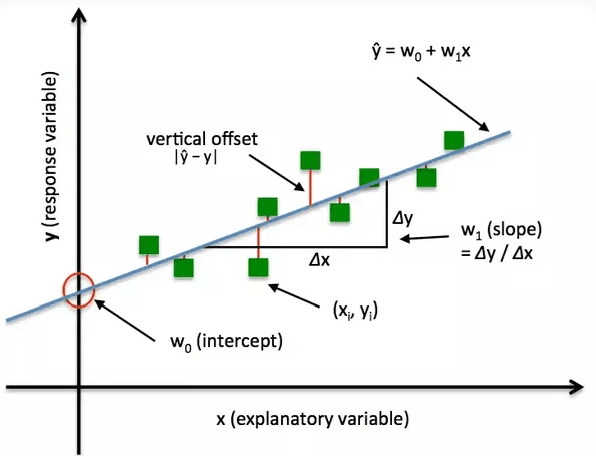
前面有提到，我們將資料輸入模型，這個模型會將輸入值配合初始化後的 weight 與 bias 計算後，而得到一個輸出值，這輸出值就是電腦「預測」的值，然而電腦預測的值還需要跟「實際」的結果做比較。一般來說，實際值跟預測值本身會存在差異值，我們便將其定義為損失 Loss。

[0]

這損失就是預測結果與真實值之間經過量化的到的指標，在統計學上又稱為「殘差」Residual。而根據上述數學式，我們一定會希望在大量模型輸入時，得出損失值越小，這樣才代表模型判斷的準確度愈高，愈具有參考價值。那在統計學上要觀察數據趨勢時，最常用的數學方法便是以下三者，我們依序來看：

數學方式[1]

1. MAE（Mean Absolute Error）數學定義如下：

其中 y 代表預測值， 代表實際值，n 代表預測的樣本數量，以下內容亦同

我們從定義中可以看到：透過計算實際與預測值之間的誤差絕對值後，再取其總和的平均值。這樣的計算便會忽略掉預測值大或小於實際值導致的方向（正負）問題。MAE 經常做為預測房價這類會追求預測與實際值之間的絕對準確性，且其對於房價的異常值的敏感度較低，較不會受到不合理的價錢所影響。

2. MSE（Mean Square Error）數學定義如下：

這個公式的不同之處，便在於計算實際值和預測值之間的「平方誤差的總和的平均值」，相對於 MAE 來說，MSE 更加強調對大誤差的敏感度。換句話說，MSE 在計算過程中很強調準確度，如股票預測等，凡是對於稍微大的偏差值就會產生很明顯的數據落差。

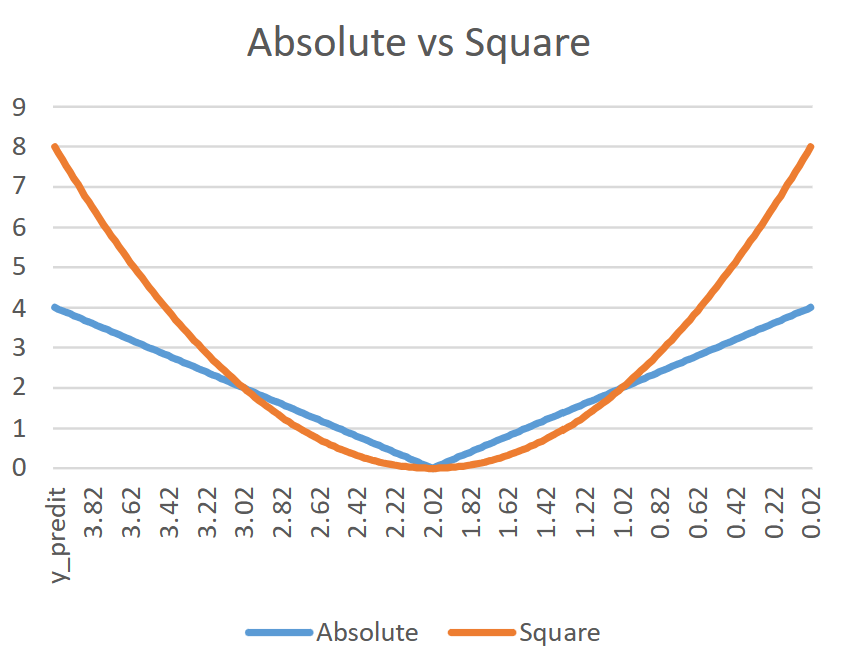
我們可以透過比較這兩個函數圖形來解釋上述內容。但要注意這是 MAE 與 MSE 還沒有執行「總和」計算的部分。

以上這些便是定義 Loss 值時，所用到最基本的函數，我們也將這函數稱為「損失函數」 Loss Function。

二、更多常用損失函數

而 Loss Function 會根據不同的問題，如二元分類、多元分類、影像與文字處理…等，都會有相對應的損失函數。我們依序來看看這些函數會選擇甚麼想法，來定義出損失函數的。

1. 分類問題

a. Entropy 代表的「熵」是甚麼？[2]

熵是來自於熱力學中，做為衡量混亂程度的標準。這個概念最早是由德國的科學家 Rudolf Clausius 所提出，他認為 Entropy 可以用來描述一個系統的混亂程度。而隨著時間的推移，Entropy 只增不減。這好比當能量在一個封閉的系統中轉換時，系統會變得趨於混亂。而當 Entropy 增加時，通常代表系統能量正在分散，使能量分布趨向於平衡。想像你把一杯熱咖啡放在房間裡，最終咖啡的熱量會分散到整個房間，使得房間的溫度變得更均勻，這就是 Entropy 增加的範例之一。

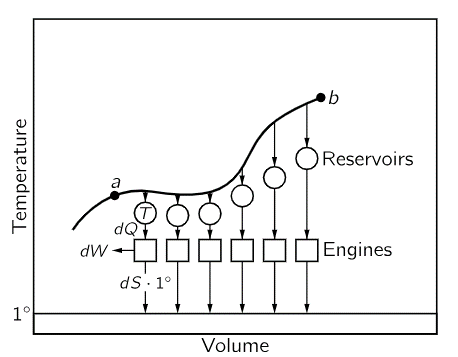
Entropy

而在我們的日常生活中，我們可以將房間中的物品想像成模型中的特徵值，而每種物品的類型（例如書、衣服、玩具等）則對應到資料的類別。如果房間裡的物品種類繁多且分佈均勻，那麼我們可以說這個房間（或者說模型）的 Entropy 較高。相反，如果房間裡只有一種物品，那麼 Entropy 就較低。這就像是我們在訓練模型時，希望模型能夠從各種特徵中學習到如何正確分類資料。

然而，如何衡量模型預測結果與真實值之間的差異呢？這就需要用到一種稱為交叉熵（Cross Entropy）的指標。Cross Entropy 主要可以分為以下兩種：

b. 二元分類：二元交叉熵 Binary Cross Entropy [3]

這就像是一個房間裡只有兩種物品（例如書和衣服）的情況。
假設書和衣服的分佈非常平均，那可以解釋為物品的分布相當「混亂」，代表 Entropy 較高；
假設房間裡幾乎全都是書，那可以解釋物品的分布相當「均勻」，代表 Entropy 就較低，因為物品的分佈較有序。

在這種情況下，BCE 就是用來衡量模型預測是書的機率，與實際上是書還是衣服的真實值，兩者之間的「混亂程度」。數學式如下：

我們假設房間裡面有兩種物品：書和衣服。我們的模型預測這個房間裡有 30% 的書和 90% 的衣服，而實際上房間裡沒有書，全都是衣服。在這種情況下，我們可以使用 Binary Cross Entropy 來看出模型預測結果與真實值之間的差異，計算方式如下：

在這裡，較低的BCE值表示模型的預測結果與實際結果更接近，因此模型的表現較好。相反地，較高的BCE值表示模型的預測結果與實際結果有較大的差異，表示模型的表現較差。

c. 多元分類：分類交叉熵 Categorical Cross Entropy

這就像是一個房間裡有很多種物品的情況，思考邏輯也與上述相同。在這種情況下，Categorical Cross Entropy 就是用來衡量模型預測是書、衣服還是其他物品的結果，與代表實際上是哪種物品的真實值，兩者之間的「混亂程度」。其數學式如下：

假設房間內有三種物品：書、衣服和玩具。我們的模型預測這個房間裡面，物體分佈的機率分別為：30% 的書，70% 的衣服、和0% 的玩具，而實際上房間裡沒有書與玩具，只有一堆衣服。在這種情況下，我們可以使用 CCE 來看出模型預測結果與真實值之間的差異，計算方式如下：

　書　：實際值 ，預測值
　衣服：實際值 ，預測值
　玩具：實際值 ，預測值

首先，我們會注意到 的值不能為零，這時我們會加上一個極小的誤差值，我們在此案中加上 使方程式合理：

由於 CCE 在處裡更龐大數量與項目的分類問題時，我們很難單純透過模型輸出的 CCE 值，來看出哪一個個體的分佈具有較明顯的特徵值，故難以判斷其預測結果是否準確，所以這時我們勢必要透過另一種方式，來將數值做一些處裡，讓這些趨勢可以更為明顯、直觀。

2. 將分類問題轉換為機率分布的 Softmax 函數

在處理多類別分類問題時，我們通常會使用 softmax 函數來將模型的原始輸出用機率值表示，意即輸出值會被壓縮在 0 到 1 之間。這樣我們就可以很直觀地看到模型對每個類別做預測的機率，這樣會更加直觀。

而 Softmax 為了確保輸出值都是正數，便在定義上透過 Exponential 函數做「正規化」，也就是說所有的值經過 Exponential 之後，可以有效凸顯出資料間的個體差異。同時也因為 Exponential 函數是連續且可微分的，這可以在後續讓機器「真正被訓練」時得以正確進行。

其中 是 j 類別中第i項的原始輸出分數。

續上題：房間內有三種物品：書、衣服和玩具。我們的模型預測這個房間裡面，物體分佈的機率分別為：30% 的書，70% 的衣服、和0% 的玩具，而實際上房間裡沒有書與玩具，只有一堆衣服。

在模型的原始輸出分數分別為 ，首先我們便將這些值放入 Softmax 做計算後得到：

這時候我們再套入 CCE 的公式做計算：

我們可以從這邊看到，經過 Softmax 轉換後的 CCE 為 0.2577，而原先單純用 CCE 的值為 0.119，這是因為模型經過 softmax 函數將原始輸出轉換為機率後，讓數值的改變能更準確反映預測與實際情況的差距。

三、結語

以上便是透過基本的 Loss Function 的介紹，我們可以從中看出來基本的 Loss Function 在簡單的數學原理之上是如何運作的。而在最後我們從 Softmax + CCE 的運算中，描述了多元分類要如何做到直觀性與準確度。然而這並不代表模型的表現變差，因為 softmax 函數只是讓數值越接近真實情況，所以只要這個值在機器學習的訓練過程中逐漸減小，就表示模型正在學習如何改進其預測結果。那在下一篇中，就會講到機器真正在訓練的「關鍵」所在。

四、參考資料

[0] Illustration of Loss: https://www.datarobot.com/blog/introduction-to-loss-functions/
[1] MAE & MSE: https://towardsdatascience.com/comparing-robustness-of-mae-mse-and-rmse-6d69da870828
[2] Feynman Lecture on Physics, CH.44-6 Entropy: https://www.feynmanlectures.caltech.edu/I_44.html
[3] BCE: https://online.stat.psu.edu/stat508/lesson/9/9.1/9.1.2