零、前言

在前面我們了解到 Deep Learning 大致上是如何運作的，那也看到我們最後測出來的準確度卻都不到 80%，嚴格說起來還不能真正地解決我們遇到的問題。那能解決這些東西的關鍵，就在於我們對於程式內參數的掌握程度。那我們要如何掌握呢？原則上就要先從其背後的運作機制開始！

一、Machine Learning的運作機制

我們可以從前面的章節中了解到，機器學習的運作機制[1]依序為定義問題、取得訓練資料、模型訓練、分析模型結果、部屬模型。而在模型訓練的過程中，又可以再細分為

1. 定義模型的結構

我們會根據問題的複雜程度與資料性質來選擇模型類型，若資料類型是屬於線性的，那我們可能會用 Linear Regression；若資料類行為非線性，那我們可能會選擇Decision Tree、或是 Neural Network 等。這樣的模型結構、或稱為函式集，會直接決定了輸入特徵與輸出預測之間的關係，而函式就代表了待分析資料在數學上的集合。

2. 從訓練資料中取得 Loss 值

損失函數的工作就是去量化訓練過程中，預測數據與實際數據之間的差異（稱作損失 Loss），換句話說就是能看出預測資料能反映真實數據的程度。損失函數並非上述之「函式集」。

3. 透過疊代做最佳化

當我們得到訓練結果時，便會再把這結果丟回去模型做訓練，藉此讓機器透過學習如何調低損失的差異，來讓準確度提升。常見的最佳化方式，就是調整會被計算的參數、或是使用類似 SGD、Adam 等最佳化器。

由此可見我們第一步要做的事情就是決定模型，我們從【Day06】的內文中可以看出，模型 Model 是由許多的 Layers 所組成，但對於該篇內文對於每一個 Layers 的運作機制的提及卻是少之又少。那在決定模型的更前提，我們首先要探討Layers其中最基礎的運作機制，便是感應器 Perceptron。

二、感應器的機制與角色

機器訓練過程的第一步驟，就要設計模型並定義模型結構。而 Perceptron 是機器學習領域中，最簡單的模型類型之一。Perceptron 的概念源自人類大腦中的 Neuron 神經細胞[3]，藉由它們接收多個輸入進行複雜的計算，並將有通過 Threshold 的資訊產生輸出。在感知器中，我們會對於這樣的結構進行模擬或想像，起初這種結構被模擬成一元一次方程式（或是你可以說線性代數），其中包含多個輸入 、權重 和偏差 。下圖中描述了其中的關係：

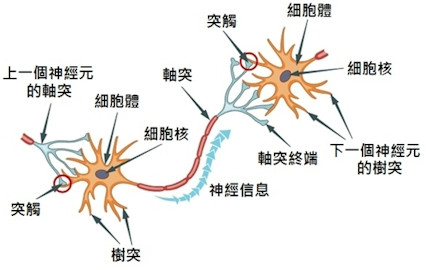
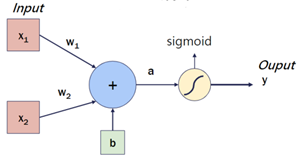
其中上圖就是根據人腦神經元所產生的基本概念。其方程式可表示為：

其中 是權重 weight，便是這個線性方程式的斜率； 是輸入變數、 是偏差值 bias。在計算過程的一開始，weight 與 bias 的值會被隨機定義，稱為初始化 Initializing，我們會再根據輸出結果是否符合預期而再做進一步的修正，當然這些程序在實務應用上，會透過一些方式讓電腦自動運作。
在現實生活中，我們經常會面臨到分類的問題，例如醫療系統要診斷患者「是健康還是不健康」的，或者我們要判斷這封電子郵件「是否」屬於 Spam，這些都屬於二元分類問題。那其實上述方程式 中，在機器的轉換下只是一串數字，所以勢必要將神經元的輸出透過一種方式做轉換，讓輸出的結果呈現兩極化，這樣就可以解決分類問題。而 Sigmoid 就解決了這樣的轉換問題：

這函數的圖形輸出如下：

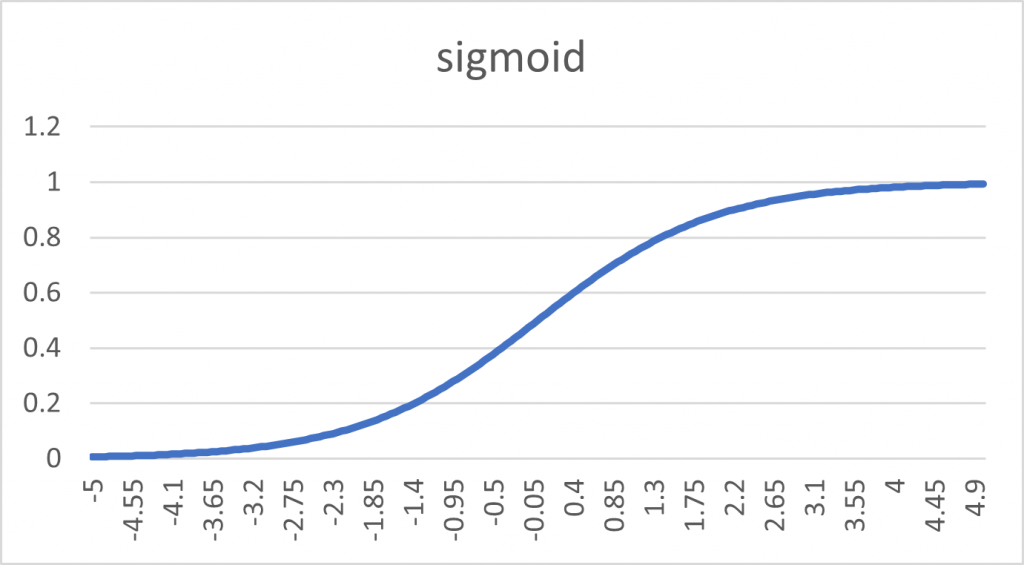
我們便可以看到輸出被分為 0 跟 1 了，可以觀察到輸出之間還是有模糊地帶，如 0.57、0.38 等數字，就很難歸類於要分在哪一類，這時前述提到的 Threshold 就是在解決這樣的問題了，透過設定 Threshold 在 0.5，便可以解決這樣不明確的狀況。

三、一個神經元有辦法解決問題嗎？

假設我們要做腫瘤診斷，腫瘤診斷可以分為「有腫瘤」、「無腫瘤」，而有腫瘤的情況又可以分為「良性」、「惡性」。單一的神經元顯然無法做這樣的預測。後來科學家發現透過一個神經元，很難解決現實生活中分類的問題。可以想像人腦的神經元機制有多複雜，但上述的結構卻是相對多簡單。後來科學家便發現只要將神經元組合在一起，這樣運作下來的機制就可以大幅提高準確度。

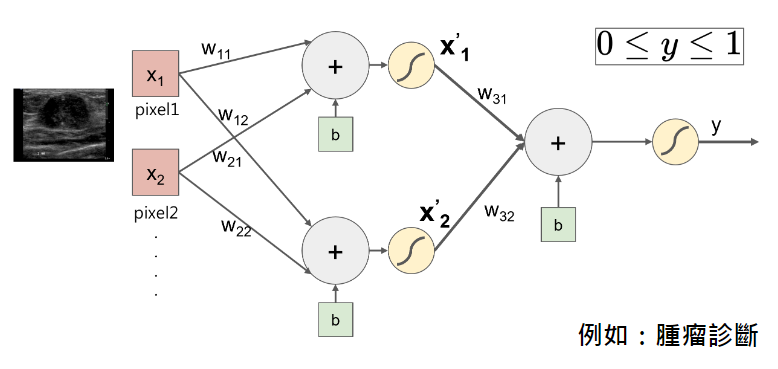
這樣多個神經元的組合，便是神經網路的雛形。在上圖中，神經網路的輸入便是圖片的每一個 Pixel值背後的數字，而經過整張圖片很多的 Pixel 輸入、且經過複查的神經元組合。我們先將上述的圖片用方程式表達：

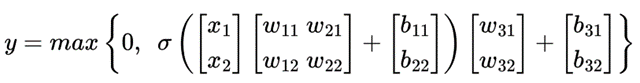
以上方程式便是藉由用 ReLU 函數來做是否有腫瘤的診斷，這會在後續文章中做說明。

四、定義模型結構

而對於多元分類問題便是把讓神經元的組合，使 的輸出不只一個，這樣便可以取得多種輸出結果了。那這時如果我們把神經網路繼續組合，就會看到 Fully Connected Neural Network 了，這結構包含了輸入層、隱藏層、以及輸出層。

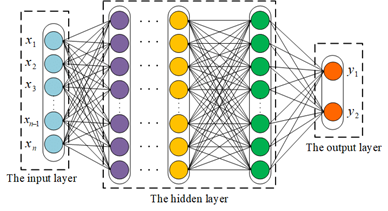
而為何中間叫做「隱藏層」呢？因為隱藏層對於輸入與輸出之間，是屬於看不到的。隱藏層在深度學習中，會學習到很多抽象的特徵．這些特徵對人類來說並不直觀，所以即便我們看到了隱藏層中每一格神經元輸出的參數，我們也難以去理解他得出結論時，其背後代表的含意。

五、結語

以上便是神經元與神經網路的關係，這樣的組合便是做為一個 Layer 成形的基礎。那要如何在這麼多變數之中找到輸入、權重、與偏差值之間的關係呢？目前有很多演算法都可以找到這些變數間的關係，而這時候最直觀的方式，便會回到數學上透過統計學的線性回歸來處理。線性迴歸是一種統計學上的模型，可以做為解決這問題的方法之一，然而在真實訓練過程中，還會涉及到很多不同的演算法來解決不同情況下的問題，這便會在下一個章節做說明。

六、參考資料

[1] Machine Learning: https://www.coursera.org/articles/what-is-machine-learning
[2] Loss Function: https://bit.ly/3utIcFm
[3] Neuron圖片: https://www.hkpe.net/hkdsepe/human_body/neuron.htm
[4] FCNN圖片: https://www.researchgate.net/figure/The-structure-of-fully-connected-neural-network-FCNN-method_fig2_342092474