零、前言

在上一篇中，我們從一些數學方法中，了解到一些基礎的 Loss Function ，如 BCE 與 CCE 是如何定義的，並且知道可以透過 Softmax 解決單純用 CCE 無法讓多項分類分布更為直觀的問題。那我們知道了 Loss Function 的機制，接下來就要思考，要透過什麼方式，使 Loss 值降低以達到更高的模型判斷的準確度呢？

一、回歸線 Regression Line

我們回顧從【Day 09】在模擬神經元運作的圖中，我們讓資料在輸出前先不經過 Softmax 運算，根據圖片的內容，便會得到以下方程式：

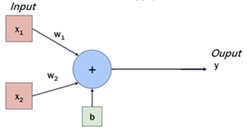
假設我們今天單純看 的組合，這是一個一元一次方程式，而權重也就是方程式的斜率，他會是一個常數，讓模型可以產生預測值（Predict Value）。在最一開始的權重是隨機設定的，當多筆資料輸入時，這個 的方程式就會產生許多對應的預測值（綠點），而這很可能畫出像下圖中的綠線一樣，跟我們資料的實際值（藍點）相差甚遠。這條綠線我們稱作「回歸線」Regression Line，而因為上述 y 與 x 的關係是一元一次方程式，所以這條綠線剛好就是我們的權重。

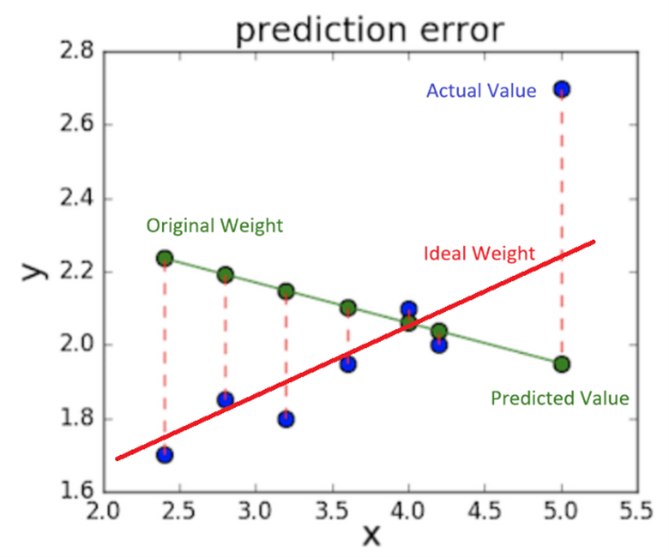
這情況代表這模型預測出來的資料，很難去反映真實情況，這就代表我們需要對權重進行調整了！而較為理想情況就會像是紅色的 Regression Line，雖然仍有一筆資料的 Loss 值很大，但卻已經能反映出大部分真實的情況了。

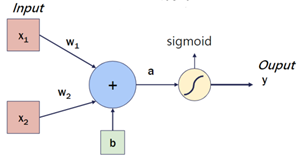
一般來說，若模型向上圖所示，那方程式會變成 ，這時 Regression Line 就會變成曲線，也就不會再與權重重疊了。所以準確來說，Regression Line 並不能完全代表 weight。而在調整權重之後，我們就可以看出來模型中的 Loss 值變少，那我們就不免要來觀察 Loss 與 Weight 之間的關係是甚麼。

二、梯度下降法 the Gradient Descent Method

權重與 Loss

我們接續上圖出發，假設我們定義要使用的 Loss Function 是 MSE，那根據 MSE 的方程式，我們可以寫出：

在這方程式中，我們已經可以看出 Loss 值與 weight 之間的關係了，這是帶有些「指數感」的二次函數，如下圖所示：

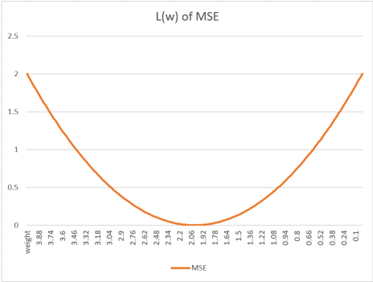
在訓練過程中，x與b都會有數值輸入，且實際值 是固定的，所以剩下的變數就會是 weight 與 Loss 值。那我們了要了解在多個 weight 值之下，每一個 weight 的變化對於輸出的 Loss 值的影響，所以我們在數學上就會對 取偏微分，也就是找出梯度 Gradient。

梯度

假設我們要找出 與 Loss 值的關係，那系統就會將 與 的值套入方程式變成常數。而我們從上式來看，就要先處理 Sigmoid 的微分

然後根據 Chain Rule 來計算 的梯度：

而其中 ，且 ，這時就可以來個別解出上面每一項的偏微分計算，而後得到：

　、　　、　

這時我們把上式結合，就會得到：

我們算出出到這方程式之後，就能看出來每一個單位的 weight 變化對於輸出的 Loss 值的影響。

三、學習率－如何更新權重？

而我們為了找出最小的值，便有了初步的構想：我們只要透過迭代的方式，向負梯度方向 推進，先計算在當前位置的梯度，減去原本的權重值 以獲得下一個權重 ，這樣的操作就可以將損失函數降到最低。（相反地，如果你希望獲得更大的誤差，那就要進行梯度加法的操作了，我們在此暫不討論這部分。）如果我們將這樣的方程式寫出來，即為：[1]

但問題來了，那這樣不免讓我們好奇的是，每一步究竟會走多大呢？

1. 為何需要學習率？[1]

在實務的機器學習過程中，如果我們無法控制梯度下降的值，那就沒有辦法去很直觀地去控制機器學習在權重更新的過程，所以我們勢必要一個參數，是可以透過人為去設定的，這樣我們才能更好地掌握機器學習的進展，並做出適當的調整。
為此我們就設定一個「超參數」Hyperparameter，這是在機器學習過程開始之前就先設定好的參數，而不是通過機器訓練而得到的。我們將這個超參數命名為「學習率」Learning Rate，代號為 。這樣我們上式就會改寫成：

2. 學習率值對訓練過程中的影響

在設定學習率之後，我們勢必就要討論學習率是如何幫助我們找到最佳解的。這時我們回顧以上方程式：

我們用一個情境讓我們更好理解數字上的意義：假設 、、，則 Loss Function 可以寫為：

我們可以劃出他的關係圖

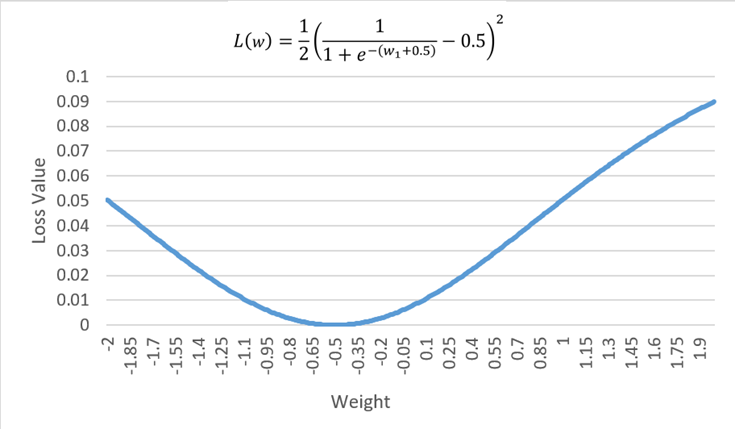
與此同時透過上述設定的參數值，以及 來計算 得到：

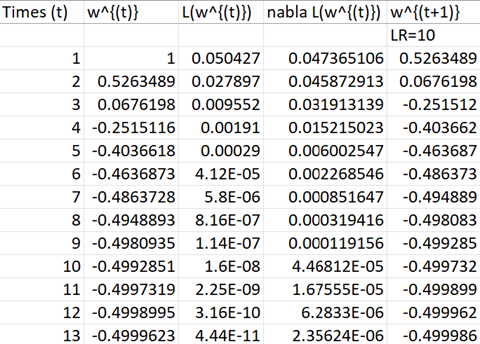
假設初始權重 我們透過計算，得出以下數據：

附上 Excel 公式參考：

L(w) = =0.5*((1+EXP(-(A302+0.5)))^(-1)-0.5 )^2
nabla L(w) = ((1+EXP(-(A302+0.5)))^(-1)-0.5)((1+EXP(-(A302+0.5)))^(-1))(1-(1+EXP(-(A302+0.5)))^(-1))

根據權重更新的 方程式，我們會寫成：

我們根據學習率的數值設定做一些討論：

a. Learning Rate 適中：

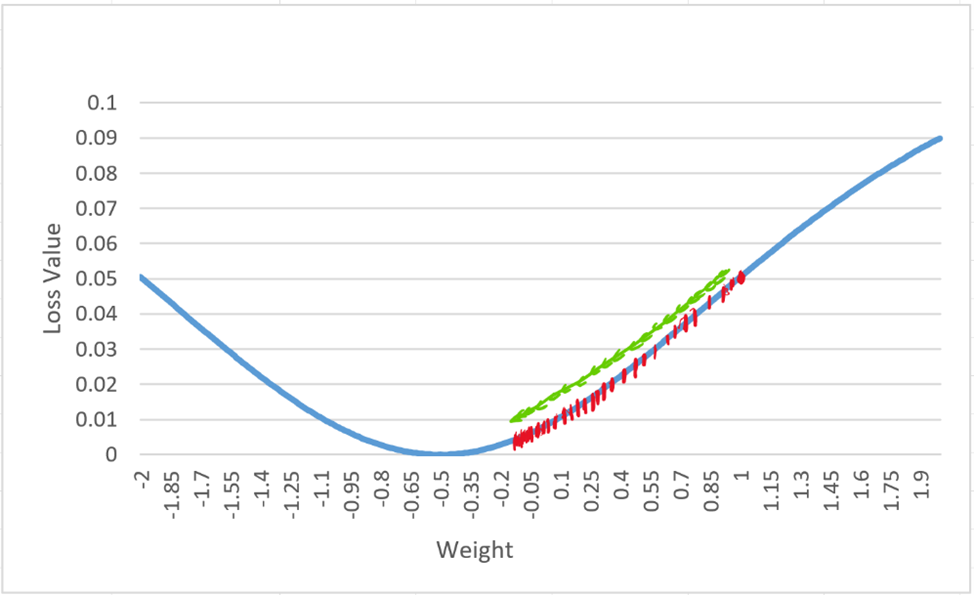
經過大約7-8 次的迭代後，我們的權重對應到的損失值就已經收斂到最低點。

b. Learning Rate 適中：

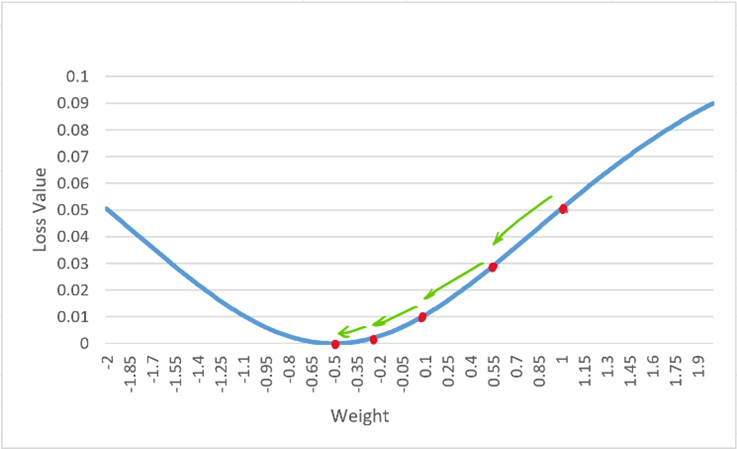
我們可以看出來在經過 30 次的迭代後，損失值仍然還沒有收斂，代表過小的學習率可能會在分析時產生效率問題。

c. Learning Rate 過大：

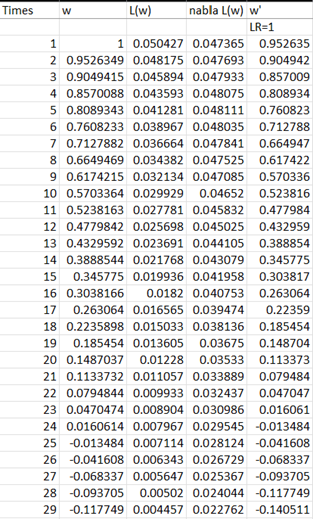
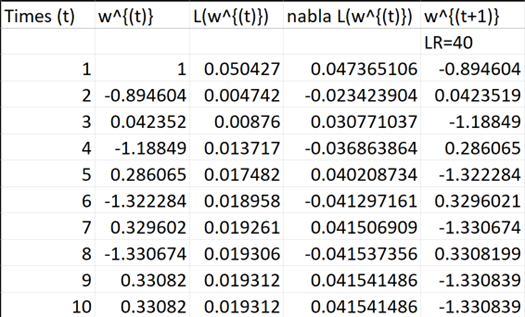
而當我們把學習率設定過大時，就會發現權重值開始「振盪」了，這樣的情況代表損失值沒有辦法收斂

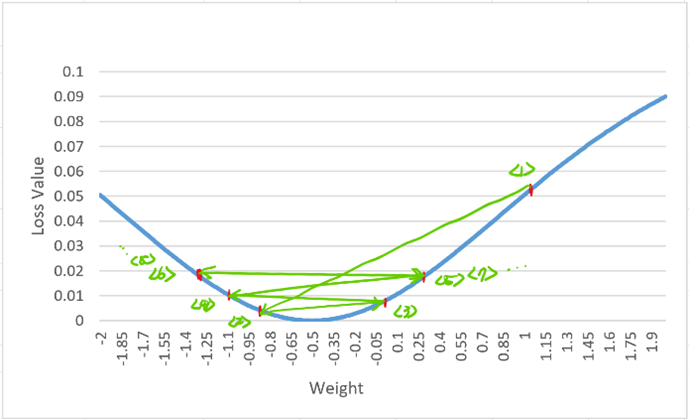
我們從以上的分析中，可以看出來學習率的設定對於機器學習的過程影響甚大，然而學習率並不會一試就成功，通常都是要反覆的調整，讓機器得以找到函數的最佳解。

四、結語

回顧整個內容，其實我自己在讀的時候，也很難看一次就真正理解機器學習過程中的數學運作。一開始我們講述權重與回歸線的關係，而後從回歸線中看出 weight的調整會對系統的 Loss 值產生影響，所以我們以 MSE 為例寫出 Loss Function 並找出梯度值，來推測如何找到最小 Loss 值，接下來就是一番數學操作找到梯度。而最佳化演算法中提供了梯度下降法，而引導出學習率對於分析過程的重要性，並以此做為找到Loss的最小值。

而文章內還沒有講述在執行梯度下降法時，可能會遇到的另外兩種找不到最小值的情況：其一是 Local Minimum，這概念在大一微積分課程中講述微分應用時會提到，亦即；其二便是 Saddle Point，情況類似於 Local Minimum，他不是極小值也並非極大值。這些應該會在下一篇中講到吧～

五、參考資料

[1] Learning Rate: https://en.wikipedia.org/wiki/Learning_rate
[2] Gradient Descent Algorithm: https://towardsdatascience.com/gradient-descent-algorithm-a-deep-dive-cf04e8115f21