一種模仿生物神經網路結構和功能數學模型或計算模型,對函數進行估計或近似。由大量類神經元聯結進行計算。大多數情況下類神經網路能在外界資訊基礎上改變內部結構,是一種自適應系統
輸入層 |
輸入層接收資料 |
|---|---|
隱藏層 |
ANN核心,包含狀態會隨著資料輸入更新 |
輸出層 |
生成ANN預測 |
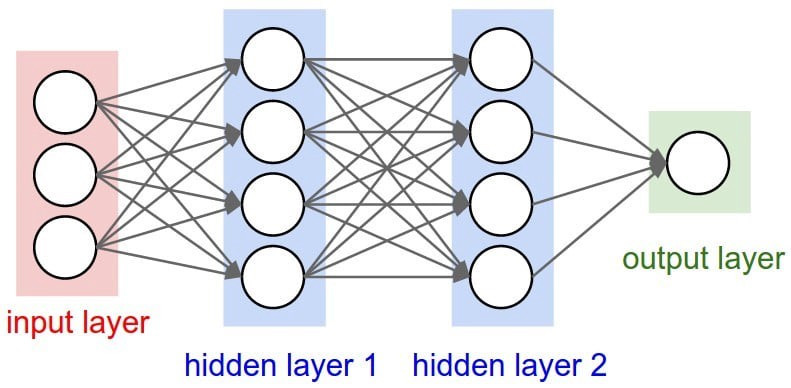
圖片來源:(https://blog.toright.com/posts/6809/keras-machine-learning-mnist/ann)
輸入資料:資料輸入類神經網路前向傳播:資料從輸入層向輸出層傳播計算誤差:計算輸出層預測與實際值誤差反向傳播:誤差從輸出層向輸入層傳播更新權重:根據誤差更新類神經網絡權重| 優點 | 缺點 |
|---|---|
| 學習複雜的函數關係 | 訓練過程可能很耗時 |
| 處理大型資料集 | 需要大量的資料 |
| 各種序列處理任務中取得高精度 | 很難解釋模型的決策 |
類神經網路是人工智能領域一個重要研究方向。隨著類神經網路技術不斷發展,將在更多領域得到應用,為我們生活帶來更多便利
節點輸出公式每個節點輸出值由輸入值和權重的加權經過激活函數處理得到
z_j = Σ_i w_ij * x_i + b_j y_j = f(z_j)
z_j |
第j個節點的輸入值 |
|---|---|
w_ij |
第i個輸入節點到第j個輸出節點權重 |
x_i |
第i個輸入節點輸出值 |
b_j |
第j個節點偏置 |
y_j |
第j個節點輸出值 |
f |
激活函數 |
輸入層公式計算輸入層節點輸出值,輸入層節點輸出值等於輸入資料值
z_i = x_i
z_i |
輸入層第 i 個節點的輸出值 |
|---|---|
x_i |
輸入資料的第 i 個特徵值 |
隱藏層公式計算隱藏層節點輸出值,隱藏層節點輸出值等於輸入值加權和再經過激活函數處理
z_j = \sum_{i=1}^{n_i} w_{ji} z_i + b_j a_j = f(z_j)
z_j |
隱藏層第 j 個節點輸出值 |
|---|---|
n_i |
輸入層節點個數 |
w_{ji} |
輸入層第 i 個節點到隱藏層第 j 個節點權重 |
b_j |
隱藏層第 j 個節點偏置 |
a_j |
隱藏層第 j 個節點激活函數輸出值 |
f |
激活函數 |
輸出層公式計算輸出層節點輸出值,輸出層節點輸出值等於輸入值加權和再經過激活函數處理
z_k = \sum_{j=1}^{n_h} w_{kj} a_j + b_k y_k = f(z_k)
z_k |
隱藏層第 j 個節點輸出值 |
|---|---|
n_h |
隱藏層節點個數 |
w_{kj} |
隱藏層第 j 個節點到輸出層第 k 個節點權重 |
b_k |
輸出層第 k 個節點偏置 |
y_k |
輸出層第 k 個節點的激活函數輸出值 |
f |
激活函數 |
用引入非線性因素,以提高神經網路的表達能力。常用激活函數包括 sigmoid函數、tanh函數 、 ReLU函數
Sigmoid函數
f(x) = \frac{1}{1 + e^{-x}}
Tanh函數
f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
ReLU函數
f(x) = max(0, x)
衡量神經網路預測值與真實值之間差異的指標。常用誤差函數包括 均方誤差(MSE) 、 交叉熵(CE)
均方誤差(MSE)
E = \frac{1}{2} \sum_{k=1}^{n_o} (y_k - t_k)^2
E |
誤差 |
|---|---|
n_o |
輸出層節點個數 |
y_k |
輸出層第 k 個節點輸出值 |
t_k |
目標值的第 k 個元素 |
交叉熵(CE)
E = -\sum_{k=1}^{n_o} t_k log(y_k) + (1 - t_k) log(1 - y_k)
E |
誤差 |
|---|---|
n_o |
輸出層節點個數 |
y_k |
輸出層第 k 個節點輸出值 |
t_k |
目標值的第 k 個元素 |
是調整神經網路參數方向和大小。常用的權重更新算法包括 梯度下降算法、RMSprop算法 、 Adam算法
梯度下降算法一種優化函數的迭代算法。在類神經網路中,梯度下降算法更新神經網路的權重
w_ij = w_ij - α * ∂E/∂w_ij
α |
學習率 |
|---|---|
E |
誤差 |
更新神經網路的權重和偏置,減小誤差。常用的權重和偏置更新公式包括 梯度下降法(GD) 、 反向傳播(BP)算法
梯度下降法(GD)
w_{ji} \leftarrow w_{ji} - \alpha \frac{\partial E}{\partial w_{ji}} b_j \leftarrow b_j - \alpha \frac{\partial E}{\partial b_j} w_{kj} \leftarrow w_{kj} - \alpha \frac{\partial E}{\partial w_{kj}} b_k \leftarrow b_k - \alpha \frac{\partial E}{\partial b_k}
w_{ji} |
輸入層第 i 個節點到隱藏層第 j 個節點權重 |
|---|---|
b_j |
隱藏層第 j 個節點偏置 |
w_{kj} |
隱藏層第 j 個節點到輸出層第 k 個節點權重 |
b_k |
輸出層第 k 個節點偏置 |
α |
學習率,一個超參數,控制權重更新的步長 |
E |
誤差或損失函數,量化了網絡預測與實際目標之間的差異 |
理解更新規則權重更新規則本質上涉及減去相應權重或偏置對應的損失函數梯度比例版本
梯度指示如何調整權重以最小化誤差方向,學習率決定調整大小
w_{ji} \leftarrow w_{ji} - \alpha \frac{\partial E}{\partial w_{ji}}
減去 學習率(α) 和 誤差(E) 對 w_{ji} 偏導數乘積更新 權重w_{ji},偏導數表示誤差對 w_{ji} 變化敏感,同樣,其他等式使用誤差相應偏導數來更新 權重w_{kj} 和 偏差b_j 和 b_k
反向傳播(Back Propagation)是從輸出層到輸入層,逐層計算各層權重和偏差梯度
\delta_j^l = \frac{\partial E}{\partial z_j^l}
w_{ij}^{l+1} \leftarrow w_{ij}^{l+1} - \alpha \delta_j^l x_i^l
b_j^l \leftarrow b_j^l - \alpha \delta_j^l
\delta_j^l |
第 l 層第 j 個節點誤差 |
|---|---|
\alpha |
學習率 |
E |
總誤差 |
RMSprop算法一種梯度下降算法的變體,通過自適應學習率來提高訓練速度
G_t = β * G_{t-1} + (1 - β) * (∂E/∂w_ij)^2 w_ij = w_ij - α * (∂E/∂w_ij) / √(G_t + ε)
β |
衰減率 |
|---|---|
ε |
平滑項 |
Adam算法一種梯度下降算法的變體,通過結合一階動量和二階動量來提高訓練速度
m_t = β_1 * m_{t-1} + (1 - β_1) * ∂E/∂w_ij v_t = β_2 * v_{t-1} + (1 - β_2) * (∂E/∂w_ij)^2 w_ij = w_ij - α * m_t / (√(v_t) + ε)
β_1 |
一階動量衰減率 |
|---|---|
β_2 |
二階動量衰減率 |
ε |
平滑項 |
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 資料準備 (假設已準備好 X_train, y_train, X_test, y_test)
# 建立模型
model = Sequential([
Dense(64, activation='relu', input_dim=X_train.shape[1]),
Dense(10, activation='softmax')
])
# 編譯模型
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
# 訓練模型
model.
fit(X_train, y_train, epochs=10, batch_size=32, validation_data=(X_test, y_test))
# 評估模型
test_loss, test_acc = model.evaluate(X_test, y_test)
print('Test accuracy:', test_acc)
人工神經網路是一種強大的工具,可以從大量數據中學習複雜的模式。隨著計算能力的提升和算法的改進,人工神經網路在越來越多的領域發揮著重要作用
資料來源:何謂 Artificial Neural Network?
