迴歸模型評估🤖

回歸模型預測出的結果為連續型的數值，預測出來的結果與真實數值兩者越接近，即模型表現較佳。今天將詳細介紹迴歸模型的評估方式。

均方誤差(Mean Square Error, MSE)🐭

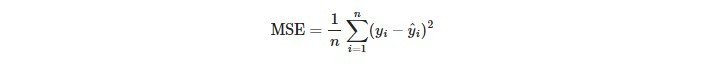
MSE是實際值與預測值之間相差的平方和取平均。MSE對於outlier會比較敏感，因為outlier會被平方後放大而導致MSE較大。MSE越趨近於0，模型表現越好。

均方根誤差(Root Mean Squared Error, RMSE)🐮

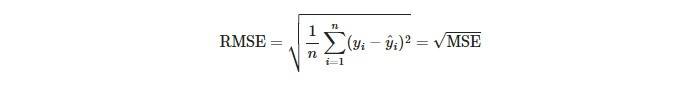
即MSE的平方根，因為有平方根所以outlier的影響程度會降低(但還是有影響)，實務上我們會評估是否需要將outlier移除再計算。RMSE越趨近於0，模型表現越好。

平均絕對誤差(Mean Absolute Error, MAE)🐯

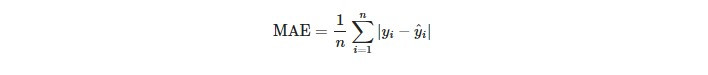
MAE是實際值與預測值之間相差的絕對值和取平均。MAE對於outlier的接受度較高，因此，MAE在有outlier的情況下比MSE更好反映模型的預測誤差。MAE越趨近於0，模型表現越好。

平均絕對百分比誤差(Mean Absolute Percentage Error, MAPE)🐰

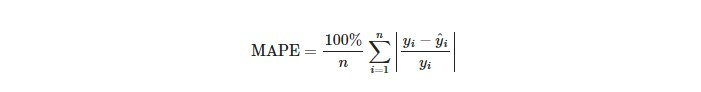
MAPE表達了預測值跟實際值的相差佔實際值的平均百分比。若實際值趨近於0時，MAPE的計算會產生非常大的誤差或無法計算。MAPE越趨近於0，模型表現越好。

決定係數(Coefficient of determination, R²)🐲

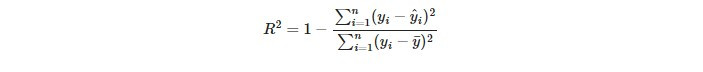
在R²的公式中，分母表示總變異量(Total Sum of Squares, SST)，即觀察值與平均值的總變異，用來衡量數據集的總變異程度。分子表示殘差變異(Sum of Squared Errors)，即觀察值與預測值之間的變異，用來衡量模型預測誤差的總和。R²是用來衡量模型解釋變異能力的指標，範圍從 0 到 1。R² 越接近 1，表示模型對數據的解釋能力越強。

實戰演練 🔥

程式碼如下：

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

# 生成假資料
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 切割數據為訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# 建立線性回歸模型
model = LinearRegression()
model.fit(X_train, y_train)

# 預測
y_pred = model.predict(X_test)

# 計算評估指標
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
mape = np.mean(np.abs((y_test - y_pred) / y_test)) * 100
r2 = r2_score(y_test, y_pred)

# 輸出結果
print(f'MSE: {mse:.2f}')
print(f'RMSE: {rmse:.2f}')
print(f'MAE: {mae:.2f}')
print(f'MAPE: {mape:.2f}%')
print(f'R^2: {r2:.2f}')

題外話 😂

最近用了一個IDE真的驚為天人，它就是Cursor
多說無益大家試過就知道它有多🐮🍺。