一種統計學方法,估計一個或多個自變數與應變數之間線性關係。也是一種廣泛使用預測建模技術,在許多領域都有應用,包括工程、經濟學、金融、生物學和社會科學
線性迴歸模型假設應變數與自變數之間的關係是線性的。應變數的值可以表示為自變數的線性組合,加上一個誤差項
y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ + ε
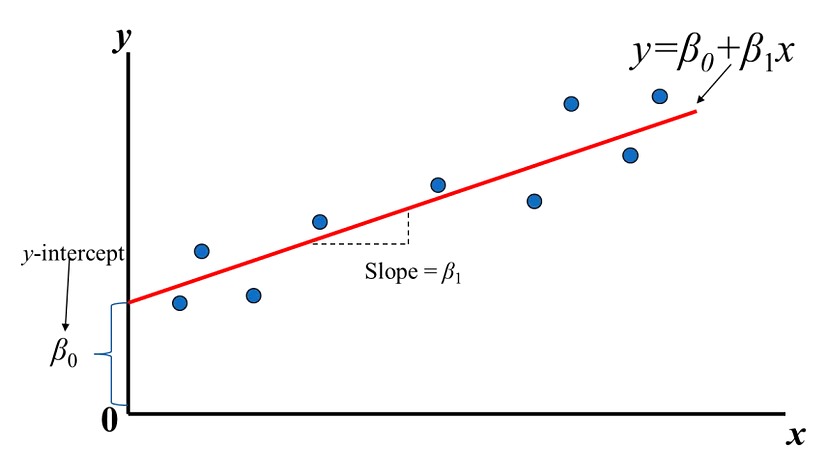
y |
應變數 |
|---|---|
x₁, x₂, ..., xₙ |
自變數 |
β₀、β₁, β₂, ..., βₙ |
回歸係數 |
ε |
誤差項 |
是指找到一組 參數β0 和 β1,使模型與觀測資料的誤差最小。最常用的擬合方法是 最小二乘法(OLS)
OLS 是一種透過最小化誤差平方和來找到最佳參數方法
β1 = Σ(xi - x̄)(yi - ȳ) / Σ(xi - x̄)^2β0 = ȳ - β1x̄
x̄ |
自變數平均值 |
|---|---|
ȳ |
應變數平均值 |
在擬合線性迴歸模型後,需要評估模型擬合效果。常用的評估指標包括:
決定係數(R^2) :表示應變數變異中有多少是由自變數解釋的。R^2的值越大,模型的擬合效果越好均方誤差(MSE) :表示模型預測值與實際值之間的平均誤差。MSE的值越小,模型的預測精度越高預測:預測房屋價格、股票價格或消費者購買量解釋:解釋教育水平與收入之間的關係或廣告支出與銷售量之間的關係控制:控制廣告支出對銷售量的影響線性關係假設:應變數與自變數之間關係是線性的如果實際關係是非線性的,則線性迴歸模型可能不準確誤差項假設:誤差項是正態分佈的。如果誤差項不符合正態分佈,則線性迴歸模型的推斷結果可能不準確多重線性迴歸:允許多個自變數非線性迴歸:允許非線性關係廣義線性模型(GLM):允許非正態分佈的誤差項import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 產生隨機數據
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 建立線性迴歸模型
model = LinearRegression(fit_intercept=True)
# 訓練模型
model.fit(X, y)
# 繪製數據點和迴歸線
plt.scatter(X, y, s=10)
plt.plot(X, model.predict(X), color='red')
plt.show()
# 顯示模型的參數
print('係數:', model.coef_)
print('截距:', model.intercept_)
線性迴歸是一種簡單但有效的統計學方法,在許多領域都有應用。然而,線性迴歸也有一些限制。在使用線性迴歸時,需要了解其限制並進行相應的處理
