支持向量機（Support Vector Machine）

一種 監督學習（Supervised Learning） 演算法，應用分類（Classification） 和 回歸（Regression） 任務。SVM是一種 最大邊距（Maximum Margin） 分類器，找到一個能夠將訓練數據中不同類別分開的最大邊距來進行分類

基本原理

是找到一個能夠將訓練數據中不同類別分開的最大邊距。所謂邊距，是指兩個 支持向量（Support Vector） 之間的距離。支持向量是那些位於邊距邊緣上的訓練數據點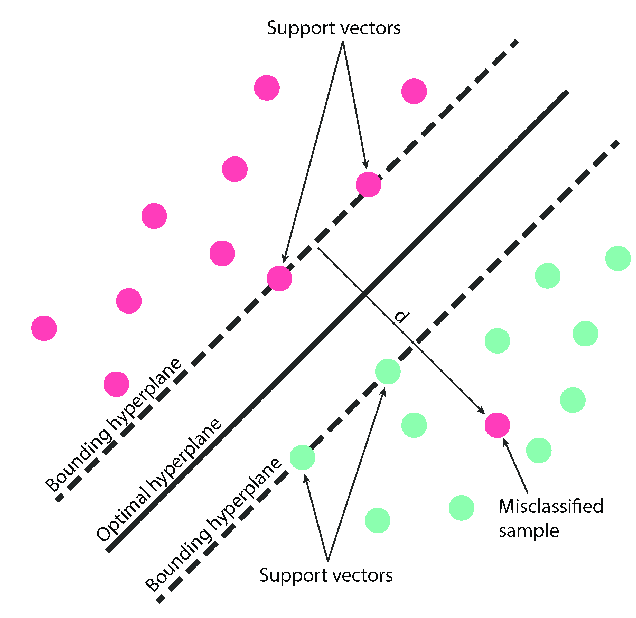

圖片來源:(https://www.researchgate.net/figure/The-support-vector-machines-SVM-method-the-optimal-hyperplane-separates-the-two_fig1_343092219)

工作原理

• 將數據映射到高維空間：需要將數據映射到高維空間才能找到一個線性邊距。這個過程可以使用 核函數（Kernel Function） 來實現
• 找到最大邊距：目標是找到一個能夠將訓練數據中不同類別分開的最大邊距。這個問題可以通過求解一個 二次規劃（Quadratic Programming） 問題來解決
• 使用支持向量進行分類：在新的數據點出現時，SVM會將其投影到高維空間，並根據其與支持向量的距離來進行分類

SVM優點缺點

SVM應用

• 圖像識別（Image Recognition）
• 生物信息學（Bioinformatics）
• 文本分類（Text Classification）
• 自然語言處理
• 數據挖掘

SVM核函數

對於線性不可分問題，通過核函數將數據映射到高維空間，在高維空間中線性可分

線性核

適合線性可分問

K(x, z) = x^Tz

多項式核

適合複雜的非線性關係

K(x, z) = (γx^Tz + r)^d

徑向基核(RBF)

適用於大多數情況，是一種非常常用的核函數

K(x, z) = exp(-γ||x-z||^2)

SVM公式

訓練數據點

{(x_i, y_i)}_(i=1,2,...,n)

超平面目標函數

min_w,b 1/2 ||w||^2 + C sum_(i=1)^n max(0, 1 - y_i(w^T x_i + b))

決策函數

sign(w^T x + b)

sign符號函數

• 輸入大於 0，則輸出
• 輸入小於 0，則輸出 -1；否則輸出 0

優化問題

min 1/2 ||w||^2 s.t. y_i(w^Tx_i + b) >= 1, i = 1, ..., n

SVM程式碼(Python-Scikit-learn)

import numpy as np
from sklearn.svm import SVC

# 訓練數據
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([1, 1, -1, -1])

# 創建 SVM 模型
clf = SVC()

# 訓練模型
clf.fit(X, y)

# 預測新數據
new_data = np.array([[9, 10]])
predicted_labels = clf.predict(new_data)
print(predicted_labels)

from sklearn.svm import SVC

# 訓練數據
X = [[1, 2], [3, 4], [5, 6]]
y = [0, 1, 2]

# 訓練模型
model = SVC()
model.fit(X, y)

# 預測新數據
new_data = [[7, 8]]
predicted_labels = model.predict(new_data)
print(predicted_labels)

範例中，使用 SVC 類別來訓練一個 SVM 模型

• fit()方法 訓練模型
• predict()方法 預測新數據

from sklearn import svm
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt

# 生成隨機數據
X, y = make_blobs(n_samples=30, centers=2, random_state=0, cluster_std=0.60)

# 建立 SVM 模型
clf = svm.SVC(kernel='linear')

# 訓練模型
clf.fit(X, y)

# 繪製決策邊界
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)

# 繪製支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
            s=80, facecolors='none', edgecolors='k')

# 繪製決策邊界
plt.axis('tight')
plt.show()

from sklearn import svm
import numpy as np

# 假設我們有兩類數據點
X = np.array([[1, 1], [2, 1], [1, 2], [2, 2], [3, 3], [4, 3]])
y = np.array([1, 1, 1, 2, 2, 2])

# 創建一個 SVM 模型
clf = svm.SVC(kernel='linear')

# 訓練模型
clf.fit(X, y)

# 預測新數據點
print(clf.predict([[2.5, 2.5]]))

總結

SVM 是一種強大的算法，可用各種機器學習任務。具有良好的泛化能力，並且對噪聲不敏感。但是，SVM 的訓練速度可能很慢，並且難以解釋