函數

函數的基本概念

首先我們來簡單理解一下什麼是函數。函數就是一段可以重複使用的程式碼，它可以幫助我們完成某個特定的任務。比如說，如果我常常需要做加法，而每次都要自己寫一長串的加法過程，那就很麻煩。
這時候我們可以寫一個函數，把加法的過程包起來，之後每次只要呼叫這個函數，電腦就會幫我們做加法的工作。

函數的格式

那我們先來看看函數是怎麼寫的吧~
可以用 def 這個關鍵字來定義一個函數。這裡有個簡單的例子：

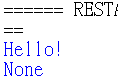
這個函數叫做 say_hello()，它的工作就是打出一個「Hello!」。只要呼叫它，
電腦就顯示出：「Hello!」。

函數的參數

參數就像是給函數的“材料”，函數會根據材料來完成工作。來看一個例子：

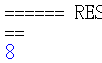
這個函數叫做 add_two_numbers(a, b)，我們可以運用數學運算，讓它幫我們把 a 和 b 兩個數字加起來，並且返回結果。最後會輸出「8」，因為 3 加 5 等於 8。

應用:找出兩數的最大公因數

設計一個程式，讓使用者輸入兩個數字，並且找出這兩個數字的最大公因數。

1. 先定義一個名叫 gcd 的函數，接收兩個參數 n1 和 n2，並找出它們的最大公因數。

2. 再來設定了一個變數 g，用來存放「目前找到的最大公因數」。一開始設成 1，是因為 1 是任何兩個數字的公因數，但我們要繼續找更大的公因數。

3. 接著設定 n 為 2，表示我們從 2 開始檢查 n1 和 n2 是否有共同的因數(因為 1 對所有數字來說都是公因數，所以要找比 1 更大的因數)。

4. 然後使用 while 迴圈來檢查 n 是否小於等於 n1 和 n2。只要 n 比這兩個數小，我們就繼續檢查它是不是兩個數的公因數。一旦 n 超過 n1 或 n2，我們就結束迴圈，因為不可能有比其中一個數更大的公因數。

5. 再來，如果 n 同時能整除 n1 和 n2（也就是兩個數對 n 的餘數都等於 0），那麼 n 就是這兩個數的公因數。當這個條件成立時，我們將 g 更新為 n，表示我們找到了新的最大公因數。

6. 每次迴圈結束後，我們將 n 加 1，這樣就可以檢查下一個可能的公因數。如果 n 最後大於 n1 或 n2，我們就停止檢查，因為更大的數不可能是公因數。

7. 當 while 迴圈結束後，g 已經是我們找到的最大公因數，所以我們用 return g 把這個值返回給主程式。

結語

一開始覺得函數有點難搞，因為要自己定義一些東西，又要學會怎麼呼叫，但現在看來，函數其實超級實用，就像是程式裡的工具箱。
比如說寫重複的代碼，之前可能要寫一大串，但是用函數的話，只要把那些重複的部分寫成一個函數，然後每次呼叫它就好，代碼瞬間變簡單又整潔>< 而且，這樣的代碼也更容易維護。出現錯誤時，只需要檢查那個函數就行，不用翻來覆去檢查每一行。

學完函數的使用後，感覺我現在寫程式的時候也變得有點「聰明」了，不會再傻傻地重複寫同樣的代碼~