簡介

我們過去探討如何利用 scikit-learn 的官方 cheatsheet 來選擇合適的演算法，並介紹了提及的演算法應用場景。然而，僅僅依賴 cheatsheet 選擇演算法還不足以滿足實際應用的需求。因此，今天我們將深入介紹幾種其他常見的機器學習演算法，包括線性回歸（Linear Regression）、決策樹（Decision Trees）、邏輯回歸 （Logistic Regression）、隨機森林（Random Forest）、以及 自適應增強（Adaptive Boosting）演算法。並分析它們的
🔍基本原理🔍：簡要說明演算法的核心思想
⚠️注意事項⚠️：提醒使用該演算法時需要注意的問題
並且將主要特點及使用場景整理成表格圖供比較。

常見演算法介紹

之前文章提過筆者實習主管說過線性回歸通常是回歸問題中第一個應該嘗試的演算法。雖然看似簡單，但這個統計方法卻蘊含深刻的意義，並在許多實際應用中發揮重要作用。因此這篇文章就讓我們從線性回歸開始吧！

1. Linear Regression（線性回歸）

• 🔍基本原理🔍：線性回歸是一種用於預測數值型目標變量的統計方法。它的核心思想是找到一條最佳的直線來描述輸入變量（特徵）和目標變量之間的關係。這條直線可以由 y = mx + b 方程式表示，其中 y 是我們想要預測的目標變量，x 是輸入變量，m 是斜率，b是截距。而線性回歸模型的目標是最小化預測值和實際值之間的差異。假設我們要預測冰淇淋店的銷量，主要考慮兩個因素：氣溫、是否是週末。如果每升高1度氣溫，銷量增加 10 個冰淇淋，週末銷量增加 50 個，我們的預測公式可能是：

冰淇淋銷量 = 10 × 氣溫 + 50（如果是週末）+ 100（基本銷量）

所以，如果今天是30度的週末，我們就可以預測：

銷量 = 10 × 30 + 50 + 100 = 450 個冰淇淋

線性回歸的核心就是找出這個最佳的「預測公式」。它通過分析大量的歷史數據，自動找出每個因素的重要性（在公式中表現為乘數），以及基本值（公式中的常數項）。

關鍵點：這個方法之所以叫「線性」回歸，是因為它假設所有因素對結果的影響都是直線關係。就像我們的例子中，我們假設溫度每升高 1 度，銷量就穩定增加 10 個。當然，現實世界往往比這個例子複雜得多。可能有更多的因素需要考慮，比如競爭對手的促銷活動、節假日等。線性回歸可以同時考慮很多因素，找出它們各自的影響程度。

• ⚠️注意事項⚠️：
  • 線性假設：假設因素與結果之間的關係是線性的。如果實際情況更複雜，模型的預測可能會不準確，也不適用於複雜的非線性關係
  • 容易受到異常值的影響：極端數據點可能會影響模型的預測結果，因此需要注意數據的清理和處理
  • 特徵之間高度相關可能導致多重共線性問題（Multicollinearity）

在許多實際應用中，線性回歸仍然是一個強大且常用的工具。它幫助我們快速得到基準結果，了解各種因素的重要性，為進一步的分析和決策提供重要參考。

2. Decision Trees（決策樹）

• 🔍基本原理🔍：決策樹是一種樹狀結構的分類或回歸模型。它是一種通過一系列的決策來進行分類或回歸的算法。它的基本思想是將數據分割成不同的子集，每個節點（或決策點）根據特徵的值來劃分數據，最終形成一棵樹狀結構。每個葉子節點表示最終的預測結果。簡單來說他就是通過一系列的是非問題將數據集劃分為越來越小的子集，直到達到一個可以做出決策的葉節點。這就像玩一個 「是非題」 遊戲，假設你在判斷是否要去戶外活動：

1) 從根節點開始，每個節點代表一個問題（如「當天是否有雨?」）。

2) 根據答案，沿著相應的分支向下。（如 「是」：結果為待在室內，「否」：繼續到下一層問題 「當天的氣溫是否超過20度?」）

3) 重複這個過程，直到達到葉節點，得到最終預測。（如 「當天的氣溫是否超過20度？」
 若為「是」：去公園散步。「否」：去咖啡館）

這樣，每次做出決策都會沿著樹的分支走，直到達到最終的預測結果。

• ⚠️注意事項⚠️：
  • 過擬合：決策樹可能會過擬合訓練數據，特別是當樹的深度過大時。可以通過剪枝來控制樹的大小
  • 不穩定性：小的數據變化可能會導致決策樹結構的大幅變化，因此需要注意模型的穩定性
  • 難以捕捉複雜的關係：對於某些非線性關係效果可能不佳

3. Logistic Regression（邏輯回歸）

邏輯回歸雖然名字上有一個 「回歸」，但邏輯回歸其實是用於解決分類問題，而非回歸問題。它之所以被稱為「回歸」，主要是因為它的數學形式和處理過程與線性回歸相似。但它的目標是通過估計機率來進行分類，而不是直接預測連續的數值。

• 🔍基本原理🔍：邏輯回歸是一種用於二元分類問題的算法。它通過計算特徵和類別之間的機率來進行預測，最終將預測結果轉化為機率值並進行分類。邏輯回歸使用邏輯函數（Logistic Function），通常是 sigmoid 函數，將輸出的機率值限制在 0 和 1 之間。目標是預測某事件發生的機率，並以此來決定分類結果。具體來說，它將特徵（如學習時間和課堂參與度）與一個線性組合結合，再通過 sigmoid 函數將這個線性組合轉化為 0 到 1 之間的機率值。舉個例子，假設你想預測學生是否會通過考試，你可以用邏輯回歸來計算學生通過考試的機率。如果模型預測的機率超過某個閾值（比如 0.5），則預測結果為「會通過考試」，否則預測為「不會通過考試」。而實際演算邏輯如下：
  假如學習時間和過去的考試成績都是影響是否通過考試的參數並且我們要預測的輸入參數值為學習時間 10 小時，過去平均分 75 分。根據這些數據，我們可以得到一個類似於線性回歸的公式如：

  分數 = 2 * 學習時間 + 0.5 * 過去平均分 - 30

  在這個例子中代入數值後：

  分數 = 2 * 10 + 0.5 * 75 - 30 = 27.5

  接下來，我們使用 sigmoid 函數將這個分數轉換為機率：

  機率 = sigmoid(27.5) ≈ 0.82

  最終做出分類：

  如果我們設定的閾值是 0.5，由於 0.82 > 0.5 ，我們預測這個學生會通過考試。

雖然邏輯回歸的過程中有類似回歸的步驟，但其最終目標是將輸入數據分類為離散的類別（如通過/不通過），而不是預測一個具體的連續值（如具體的考試分數）。

• ⚠️注意事項⚠️：
  • 需要假設特徵和標籤之間存在線性關係
  • 對異常值敏感
  • 需要處理特徵之間的多重共線性
  • 主要用於二元分類：雖然可以擴展到多類別，如多項邏輯回歸（Multinomial Logistic Regression），但主要強項是區分兩種結果
  • 假設特徵間關係是線性的：如果實際關係很複雜，可能需要其他方法
  • 需要足夠的數據：才能準確學習特徵和結果之間的關係

4. Random Forest（隨機森林）

• 🔍基本原理🔍：隨機森林是一種基於決策樹的集成學習算法，用於分類和回歸問題。它通過構建多棵決策樹來進行預測。每棵樹是從數據的隨機子集和隨機特徵中生成的。最終的預測結果是所有樹的預測結果的平均值（回歸）或多數決（分類）。隨機森林的關鍵思想是通過引入隨機性來增強模型的泛化能力，減少過擬合的風險。假設我們要預測一個人是否會購買某個產品。隨機森林可能會這樣工作：

1. 生成多棵決策樹：

    樹 1 可能使用年齡和收入作為特徵 

    樹 2 可能使用職業和教育程度作為特徵 

    樹 3 可能使用家庭狀況和居住地區作為特徵 

2. 每棵樹獨立做出預測：

    樹 1 預測：會購買 

    樹 2 預測：不會購買 

    樹 3 預測：會購買 

綜合所有樹的預測：

由於多數樹預測「會購買」，最終預測結果是這個人會購買產品。

這種方法的優勢在於，即使某些特徵或某棵樹的預測不準確，整體預測仍可能是準確的。

• ⚠️注意事項⚠️：
  • 計算複雜度高，訓練時間可能較長
  • 對於很小的數據集可能會過擬合
  • 模型解釋性不如單一決策樹

5. Adaptive Boosting（Adaboost，自適應增強）

• 🔍基本原理🔍：Adaboost 是一種集成學習方法，它通過迭代的方式來提升模型的準確性。每次迭代中，Adaboost 會調整樣本的權重，重點關注那些被前一輪模型錯誤分類的樣本，從而生成一個更強大的模型。假設我們要開發一個垃圾郵件檢測系統。Adaboost可能會這樣工作：

1. 第一輪：
   使用一個簡單的規則（如檢查是否包含「免費」這個詞）
   假設這個規則正確分類了 60% 的郵件

2. 第二輪：
   增加那些被錯誤分類郵件的權重
   新增一個規則（如檢查發件人地址）

這個規則可能在剩下的難分類郵件中正確分類了 70%

3. 第三輪：
   再次調整權重，關注更難分類的郵件
   添加更複雜的規則（如分析郵件內容的語義）

4)最終模型： 綜合所有規則，賦予每個規則不同的權重，形成一個強大的分類器。

這種方法的優勢在於它能夠逐步關注難以分類的樣本，從而不斷提高整體分類性能。

• ⚠️注意事項⚠️：
  • 對異常值和噪聲數據敏感，雖然對一定噪音魯棒，但過多的噪音可能會影響模型效果
  • 計算複雜度隨迭代次數增加而增加
  • 基學習器的選擇會影響整體性能

結論

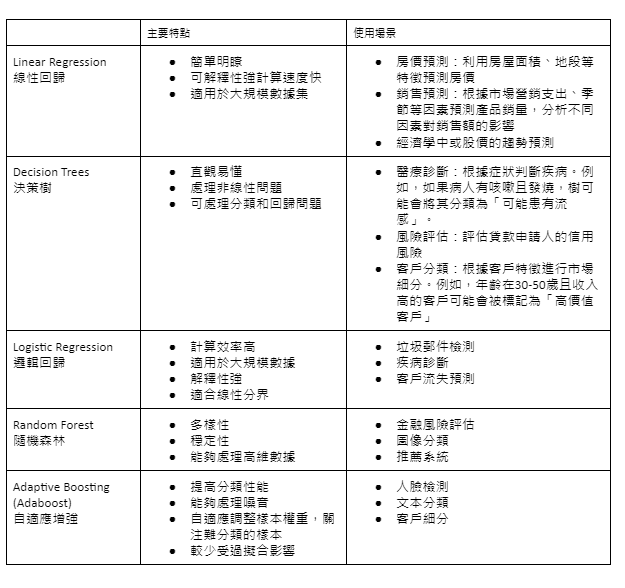
在實際應用中，通常需要對多個演算法進行比較和測試，以找到最佳解決方案。此外，我們還需要關注數據的質量和特徵工程，這些都對模型的效果影響很大。總結來說，機器學習演算法的選擇和應用是一個需要綜合考慮多方面因素的過程。在下一篇文章中，我們將深入探討如何進行模型比較，這將涉及到機器學習中最重要的評估階段。選擇合適的算法只是成功應用機器學習的第一步，後續的評估、優化和部署同樣重要。