簡介

在上一篇文章中，我們了解了如何通過自動識別數據中的隱含結構來實現數據的分組。今天，我們將繼續探討無監督學習中的另一個重要技術領域：降維演算法。

降維的目標是簡化數據結構，使高維數據在低維空間中更易於理解和處理。想像一下，我們有一個包含大量特徵的數據集，而這些特徵中有許多可能是多餘的或無關緊要的。降維技術就像是將這些多餘的特徵去除，只保留那些最重要的資訊。在本篇文章中，我們將介紹幾種 Scikit-learn Cheatsheet 提供的降維演算法，包括隨機化主成分分析（Randomized PCA）、等度量映射（Isomap）、譜嵌入（Spectral Embedding）、核近似（Kernel Approximation）、以及局部線性嵌入（LLE）。我們將深入探討這些算法的：
🔍基本原理🔍：簡要說明演算法的核心思想
⚠️注意事項⚠️：提醒使用該演算法時需要注意的問題
並且將主要特點及使用場景整理成表格圖供比較。

Cheatsheet 中的演算法介紹 - 降維

在深入了解各種降維演算法之前，我們需要了解這些演算法的共同目標：在儘量保留原始數據核心資訊和結構的情況下，降低數據的維度。降維技術可以幫助我們處理高維數據，提升計算效率，同時揭示數據中的潛在模式。之前的文章有提過，人類可以直觀地理解最多三維的數據，超過這個範圍後就很難想像。同樣地，機器學習模型中的參數量增加會使模型變得更複雜，這可能導致計算困難或過擬合。因此，降維技術可以幫助我們在保持重要特徵的同時簡化數據結構，也可以視為一種特徵選擇的方式。

1. Randomized PCA (隨機化主成分分析)

• 🔍基本原理🔍：Randomized PCA 是一種改進版的主成分分析（PCA）方法，用於處理高維數據。傳統 PCA 需要進行大量計算來找出數據的主要成分，而隨機化 PCA 通過隨機投影的方式，能夠更快地估算這些主要成分。這就像在一個非常大的圖書館裡，你想找到最重要且最受歡迎的書籍，Randomized PCA 就像：

1) 隨機走到幾個書架前，這些書架代表圖書館中的一些樣本

2) 在每個選中的書架上，查看最受歡迎的書籍類型，並記錄這些類型的資訊

3) 根據這些選中的書架上的書籍類型，你推斷出整個圖書館中主要的書籍類型

4) 為了確保你的估算準確，你會多次隨機挑選書架並分析，然後將所有結果進行平均，以獲得更穩定的估算

Randomized PCA 就利用這種隨機挑選和平均的方式，快速而高效地估算出數據的主要特徵，而不必進行全數據集的繁瑣計算。

• ⚠️注意事項⚠️：
  • 由於是隨機化的過程，結果可能會有所不同，因此需要多次運算來確保結果的一致性
  • 可能會忽略一些細節，就像可能會漏掉一些稀有的書籍類型
  • 對特徵量本來就少的就不需要使用，就像對小型圖書館效果可能會不佳，如果藏書量小，還是全面檢查比較準確

2. Isomap (等度量映射)

• 🔍基本原理🔍：Isomap 是一種非線性降維技術，用於保持數據中點與點之間的距離。想像你在一個大型的城市地圖上，等度量映射就像是將這個城市的地圖簡化成一個小型的平面地圖，同時保留每個城市之間的實際距離。它通過計算每個點的最短路徑來確保在低維空間中仍能保留原始數據的幾何結構。Isomap 就像：

1) 在地球表面標記重要地點：你首先在地球上標記一些重要的地點，這些地點代表你要關注的數據點

2) 計算這些地點之間的實際距離：你計算這些地點之間沿著地球表面的實際距離，這些距離反映了數據點之間的相似度

3) 在平面紙上放置這些地點：然後，你嘗試在一張平面紙上放置這些地點，使它們之間的距離盡可能與實際距離相符。這個過程就像是在低維空間中進行嵌入，儘量保留原始距離資訊

4) 推斷其他地點的位置：根據這些主要地點在平面上的位置，你可以推斷出其他尚未標記的地點在平面上的位置

• ⚠️注意事項⚠️：
  • 計算成本高：對於大型數據集，計算距離矩陣可能很耗時
  • 對噪聲敏感：就像地圖製作中的測量誤差可能導致整體失真
  • 需要選擇適當的鄰居數量：就像選擇多少個主要地點來繪製地圖

3. Spectral Embedding (譜嵌入)

• 🔍基本原理🔍： Spectral Embedding 也是一種非線性降維方法，它利用數據的相似度圖的特徵向量進行降維。它會先計算數據點之間的相似度，然後進行矩陣分解，將數據映射到低維空間中。想像你有一張結構圖，圖中的點表示數據，邊表示點之間的相似度。譜嵌入通過分析這張結構圖來找到一個低維空間中的表示方式，保持點之間的關係。這種方法可以很好地處理數據中的複雜結構。假如你是一位音樂製作人，需要將一首複雜的交響樂簡化為幾個主要的音樂元素：

1) 將音樂分解為頻率成分：首先將整首複雜的交響樂分解為不同的頻率成分，就像在數據中構建一個相似性圖，其中每個音符或和弦代表一個數據點

2) 找出最重要的頻率成分：接著，識別出最重要的幾個頻率，這些頻率成分代表了音樂的主要特徵。這一步類似於計算拉普拉斯矩陣的特徵向量，這些特徵向量揭示了數據的主要結構

3) 用主要頻率重組樂曲：最後，用這些主要頻率重新組合，創造一個簡化版的樂曲。這就像在低維空間中重建數據，保留了原始音樂的主要結構和特徵，而忽略了細節部分

• ⚠️注意事項⚠️：
  • 對參數敏感：結果可能受到相似性度量選擇的影響，需要選擇適當的相似度度量和圖構建方法，以確保結果的準確性和效果
  • 可能不適合非常大的數據集：需要計算整個數據集的相似性矩陣

4. Kernel Approximation (核近似)

• 🔍基本原理🔍：Kernel Approximation 是一種通過近似高維空間中的映射來進行降維的方法，但不直接計算高維空間中的坐標。假設你有一個數據集，通過核函數將數據映射到高維空間，再在高維空間中進行簡化，這樣可以保留數據的主要特徵。常見的核近似方法包括 Random Kitchen Sinks 和 Nystroem 方法，它們能夠有效地近似這些高維映射，從而保留數據的主要結構並提高計算效率。Kernel Approximation 就像：

1) 你有一份複雜的食譜（原始數據）：這些食譜步驟可能很複雜，直接製作需要很多時間和精力

2) 你決定使用預製的調味料（核函數）：這些預製調味料就像核函數，它們可以簡化烹飪過程。調味料能模擬複雜的烹飪步驟，讓你能更輕鬆地達到類似的效果

3) 製作過程簡化，但最終菜餚味道相似：雖然過程變得簡單許多，但你得到的最終菜餚仍然保持了原有的味道。這樣，你能在保持主要特徵的同時，減少計算複雜度

• ⚠️注意事項⚠️：
  • 近似性：結果是對真實高維映射的近似，可能會損失一些精度
  • 核函數選擇：不同的核函數可能導致不同的結果，需要根據數據特性選擇

5. Locally linear embedding（LLE，局部線性嵌入）

• 🔍基本原理🔍：LLE 是一種保持數據局部結構的降維方法。假設你有一個數據點，它的周圍有一些相似的點。LLE 會保留這些相似點之間的關係，然後在低維空間中重建這些關係，這樣可以保持數據的局部結構。LLE就像：

1) 記錄每塊拼圖與周圍拼圖的相對位置： 你首先確定每塊拼圖與它周圍的拼圖之間的相對位置，就像找到每個數據點的近鄰

2) 計算如何用周圍的拼圖來表示每一塊拼圖： 接著，你計算如何用周圍的拼圖來描述每一塊拼圖的位置和形狀，這相當於計算重建權重

3) 在2D平面上重新排列這些拼圖，盡量保持它們之間的相對關係： 最後，你將這些拼圖在一個2D平面上進行重新排列，努力保持它們之間的相對位置和關係不變，這就是低維重建

• ⚠️注意事項⚠️：
  • 對噪聲敏感：局部結構的擾動可能影響全局結果
  • 計算成本：對於大型數據集，計算鄰居關係可能很耗時
  • 輸出不唯一：不同運行可能產生略有不同的結果

結論

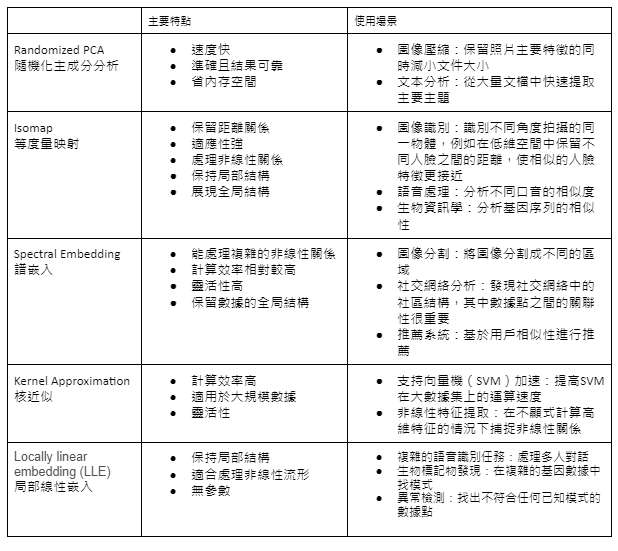
降維技術在處理高維數據時，不僅能降低計算複雜度，還能提升模型的性能和數據可視化的效果。這些方法為我們提供了多種選擇，根據不同的數據特性和應用需求，可以靈活選用最適合的降維技術。在下一篇文章中，我們將繼續介紹一些 Scikit-learn Cheatsheet 沒有提到的其他常見演算法，進一步豐富我們對機器學習技術的認識與應用。