在上一篇文章中,我們介紹了線性回歸(Linear Regression)的基本概念。接下來,我們將通過一個實際範例來演示線性回歸的應用。本範例使用 Python 的 sklearn 套件,數據來源為臺北市政府民政局提供的臺北市歷年出生及死亡人口數。選擇這組資料的原因主要是因為我無法找到更合適的公開數據,而本文重點在於展示機器學習的框架與算法,因此我希望能減少在數據預處理方面的工作量。
首先,我們將資料用表格和圖表的方式展示出來:
| 年 | 出生人數 | 死亡人數 |
|---|---|---|
| 57年 | 40,923 | 6,471 |
| 58年 | 41,667 | 6,365 |
| 59年 | 45,078 | 6,574 |
| 60年 | 43,542 | 6,769 |
| 61年 | 42,252 | 6,869 |
| 62年 | 41,998 | 7,005 |
| 63年 | 43,113 | 7,312 |
| 64年 | 41,710 | 7,333 |
| 65年 | 48,284 | 7,433 |
| 66年 | 43,229 | 7,977 |
| 67年 | 44,124 | 7,908 |
| 68年 | 45,978 | 8,149 |
| 69年 | 43,998 | 8,188 |
| 70年 | 44,019 | 8,548 |
| 71年 | 42,948 | 8,653 |
| 72年 | 40,917 | 8,945 |
| 73年 | 40,142 | 8,957 |
| 74年 | 38,984 | 9,198 |
| 75年 | 35,542 | 9,218 |
| 76年 | 36,799 | 9,740 |
| 77年 | 41,040 | 10,300 |
| 78年 | 38,343 | 10,296 |
| 79年 | 39,601 | 10,631 |
| 80年 | 36,538 | 10,614 |
| 81年 | 35,310 | 11,011 |
| 82年 | 34,374 | 11,025 |
| 83年 | 33,605 | 11,245 |
| 84年 | 34,763 | 11,809 |
| 85年 | 34,151 | 12,221 |
| 86年 | 35,062 | 12,359 |
| 87年 | 30,203 | 12,374 |
| 88年 | 31,812 | 12,669 |
| 89年 | 33,678 | 12,989 |
| 90年 | 26,998 | 13,337 |
| 91年 | 25,647 | 13,522 |
| 92年 | 23,311 | 13,777 |
| 93年 | 22,154 | 14,016 |
| 94年 | 20,962 | 14,516 |
| 95年 | 21,151 | 14,011 |
| 96年 | 21,620 | 14,871 |
| 97年 | 20,691 | 15,606 |
| 98年 | 19,403 | 15,260 |
| 99年 | 18,530 | 15,398 |
| 100年 | 25,132 | 15,988 |
| 101年 | 29,498 | 16,579 |
| 102年 | 26,710 | 16,379 |
| 103年 | 29,024 | 17,177 |
| 104年 | 28,987 | 17,106 |
| 105年 | 27,992 | 17,982 |
| 106年 | 25,042 | 17,467 |
| 107年 | 22,849 | 17,902 |
| 108年 | 21,468 | 18,026 |
| 109年 | 19,029 | 17,212 |
| 110年 | 16,695 | 18,623 |
| 111年 | 14,528 | 20,783 |
| 112年 | 16,027 | 20,357 |
這些數據展示了臺北市近幾十年的出生與死亡人數。我們假設出生人數和死亡人數之間可能存在某種關聯,因為每個人最終都會死亡,所以我們可以嘗試通過出生人數來預測死亡人數。然而,需要強調的是我們此次使用的模型可能不夠合理,具體的理由將在文章結尾進一步解釋。
首先,我們可以用程式生成圖表:
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib.font_manager import fontManager
fontManager.addfont('ChineseFont.ttf')
mpl.rc('font', family='ChineseFont')
census = pd.read_excel('born_and_death.xlsx')
x = census['出生人數']
y = census['死亡人數']
plt.title('臺北市出生與死亡人數')
plt.xlabel('出生(人)')
plt.xlim(12000, 50000)
plt.ylabel('死亡(人)')
plt.ylim(5000, 23000)
plt.scatter(x, y)
plt.show()
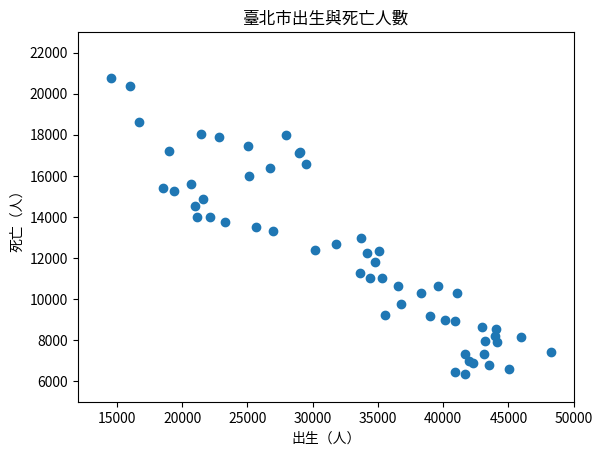
接下來,我們將數據分成訓練集和測試集,使用 sklearn 的 train_test_split 方法進行分割:
from sklearn.model_selection import train_test_split
# 分割Training Data和Testing Data
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=55)
在這裡,我們將數據分為訓練集(X_train, y_train)和測試集(X_test, y_test)。test_size=0.2 表示將整個數據集的20%作為測試數據,而 random_state 是為了固定隨機分割的結果,這樣可以讓他人復現你的結果。
使用 sklearn 的線性回歸模型進行訓練:
from sklearn.linear_model import LinearRegression
# 建立線性回歸模型
model = LinearRegression()
# 用分割出的Training Data訓練模型
model.fit(X_train, y_train)
使用訓練好的模型進行預測:
# 進行預測
y_pred = model.predict(X_test)
我們可以使用 MSE(均方誤差)來評估模型的效果:
from sklearn.metrics import mean_squared_error
# 評估模型
mse = mean_squared_error(y_test, y_pred)
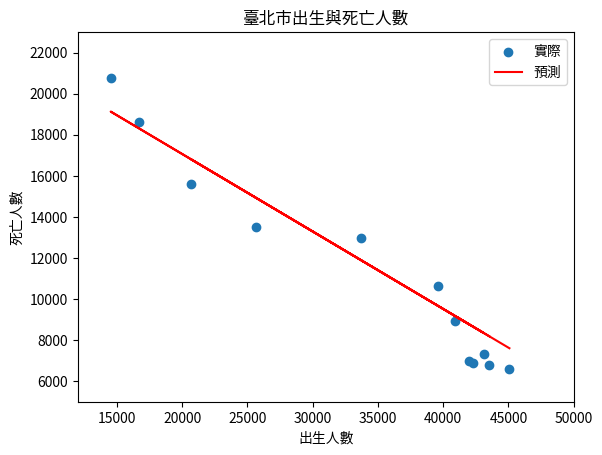
最後,我們將結果打印出來並畫出統計圖來展示成果:
# 視覺化
print('Mean Squared Error:', mse)
print('w', model.coef_[0])
print('b', model.intercept_)
plt.scatter(X_test, y_test, label='實際')
plt.plot(X_test, y_pred, color='red', label='預測')
plt.title('臺北市出生與死亡人數')
plt.xlabel('出生人數')
plt.ylabel('死亡人數')
plt.xlim(12000, 50000)
plt.ylim(5000, 23000)
plt.legend()
plt.show()
結果顯示:
我們也可以嘗試去掉 random_state,將會得到不同的結果(因為資料的切割是隨機的):
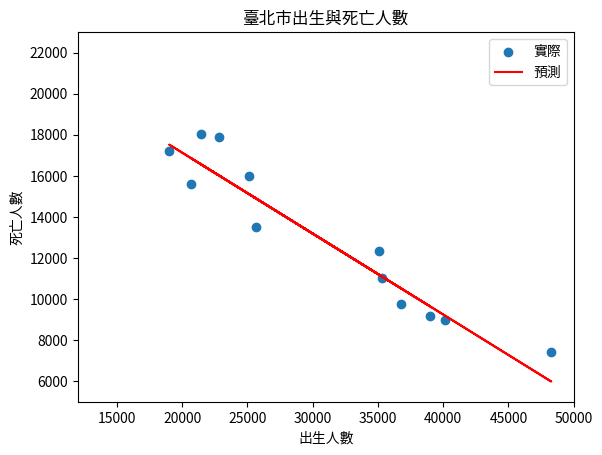
可以看到,這次的結果與上次不同。
附上完整程式碼,供參考:
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 讀取資料
census = pd.read_excel('born_and_death.xlsx')
# 特徵工程
X = census[['出生人數']]
y = census['死亡人數']
# 分割Training Data和Testing Data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=55)
# 建立線性迴歸模型(這邊就直接使用套件而不實作了)
model = LinearRegression()
# 用先前分割的Training Data訓練模型
model.fit(X_train, y_train)
# 進行預測
y_pred = model.predict(X_test)
# 評估模型好壞
mse = mean_squared_error(y_test, y_pred)
# 視覺化
print('Mean Squared Error:', mse)
print('w', model.coef_[0])
print('b', model.intercept_)
plt.scatter(X_test, y_test, label='實際')
plt.plot(X_test, y_pred, color='red', label='預測')
plt.title('臺北市出生與死亡人數')
plt.xlabel('出生人數')
plt.ylabel('死亡人數')
plt.xlim(12000, 50000)
plt.ylim(5000, 23000)
plt.legend()
plt.show()
在前文中提到,我們使用的模型可能不夠合理。這是因為一般人的平均壽命大約在70到80歲之間(內政部:111年國人平均壽命79.84歲),而我們的數據統計範圍為57年到112年,共55年,這些數據無法真實反映出生與死亡人數之間的關係。但這個實驗對於練習簡單的線性回歸仍然是有價值的。今天的文章就到這裡,期待下一篇文章的分享。
