在上一篇文章中,我們介紹了分類問題的常見評估指標。今天,我們將進一步探討回歸、聚類與降維問題的評估指標,以及如何進行模型比較,幫助我們選擇最合適的模型。

[source: meme-arsenal]
回歸問題的評估指標
回歸問題主要涉及連續數值的預測,常見的評估指標包括:
-
均方誤差(Mean Squared Error, MSE):MSE 衡量了預測值與真實值之間的平均平方差異。它反映了模型預測值與真實值之間的距離,值越小越好。例如,在房價預測中,如果模型預測的房價與實際房價相差不大,MSE 就會較小。
-
公式: ,其中 y_i 為真實數據, ŷ_i 為預測數據
,其中 y_i 為真實數據, ŷ_i 為預測數據
-
使用時機:當我們希望對大誤差給予更多懲罰時,或者當數據中的離群值對分析很重要時。
-
代表含義:MSE 越小,模型的預測效果越好,誤差越小表示模型的預測越準確。
-
注意事項:MSE 對離群值很敏感,可能會導致模型過度關注極端情況。
-
均方根誤差(Root Mean Squared Error, RMSE):RMSE 是 MSE 的平方根,它提供了一個與原始數據單位相同的誤差度量,使得解釋更加直觀。
- 公式:RMSE = √MSE
- 使用時機:當我們需要一個與原始數據單位相同的誤差度量,使得解釋更加直觀時。
- 代表含義:RMSE 越小,模型的預測精度越高。
- 注意事項:與 MSE 相同,RMSE 對極端值敏感。
-
平均絕對誤差(Mean Absolute Error, MAE):MAE 是預測值與真實值之間絕對差值的平均值,反映了平均預測誤差。與 MSE 不同,它不會放大較大誤差的影響,是一個更穩健的指標。它在量級上與原始數據保持一致,因此更容易解釋。
- 公式:
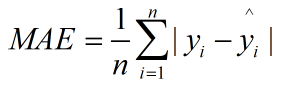 ,其中 y_i 為真實數據, ŷ_i 為預測數據
,其中 y_i 為真實數據, ŷ_i 為預測數據
- 使用時機:當我們希望以相同的方式對待所有誤差,不特別強調大誤差時。
- 代表含義:MAE 越小,模型的預測效果越好。
- 注意事項:MAE 對極端值不如 MSE 和 RMSE 敏感,可能更適合在存在離群值的數據集中使用。
-
R 平方(R-squared, R²):R 平方,又稱決定係數,是衡量模型解釋變異比例的指標。它表示模型預測值與實際值之間的相關性,數值範圍在 0 到 1 之間,越接近 1 表示模型解釋能力越強。
- 公式:
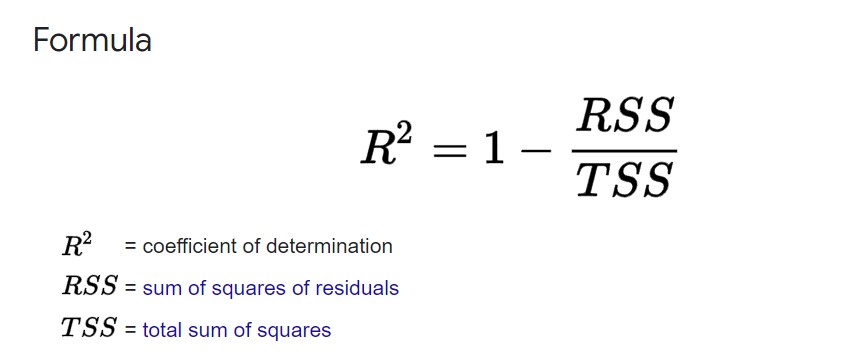
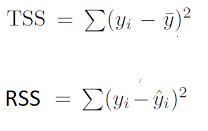 ,其中 y_i 為實際值,ŷ_i 為預測值,ȳ 為實際值的平均數
,其中 y_i 為實際值,ŷ_i 為預測值,ȳ 為實際值的平均數
- 使用時機:當我們想要知道模型解釋了多少輸出變異時。
- 代表含義:R² 越接近 1,表示模型對輸出變異的解釋能力越強。0 表示模型無法解釋輸出變異,1 表示模型能完美解釋輸出變異。
- 注意事項:R² 不適合用於比較不同數據集的模型,因為它受到數據集變異性的影響。R² 可能會因為加入無關變量而人為增加,因此在使用時需要謹慎。
來舉個例子,假設我們正在開發一個回歸模型來預測房屋的價格(單位:百萬台幣),根據一些房屋的特徵,例如房屋的面積、房齡、和房間數量。以下是實際的房價和我們模型的預測結果:
| 房屋 |
實際房價 (百萬台幣) y |
預測房價 (百萬台幣) ŷ |
| A |
3.0 |
2.8 |
| B |
4.5 |
4.2 |
| C |
6.0 |
5.9 |
| D |
8.0 |
8.1 |
| E |
10.0 |
10.5 |
我們希望評估這個模型的性能,並使用以下指標:MSE、RMSE、MAE 和 R²
a) MSE = 1/5[(3.0-2.8)² + (4.5-4.2)² + (6.0-5.9)² + (8.0-8.1)² + (10.0-10.5)²] = 1/5[0.04 + 0.09 + 0.01 + 0.01 + 0.25] = 0.08
b) RMSE = sqrt (MSE) = sqrt(0.08) ≈ 0.283
c) MAE = 1/5[∣3.0−2.8∣+∣4.5−4.2∣+∣6.0−5.9∣+∣8.0−8.1∣+∣10.0−10.5∣] = 1.2/5 = 0.24
計算 R² 之前要先算實際數值的平均數:ȳ = 1/5 (3.0+4.5+6.0+8.0+10.0) = 6.3,接著算 RSS = (3.0-2.8)² + (4.5-4.2)² + (6.0-5.9)² + (8.0-8.1)² + (10.0-10.5)² = 0.4,接著算 TSS = (3.0-6.3)² + (4.5-6.3)² + (6.0-6.3)² + (8.0-6.3)² + (10.0-6.3)² = = 10.89 + 3.24 + 0.09 + 2.89 + 13.69 = 30.8。最終計算 R² = 1- (0.4/30.8) ≈ 0.987
計算完以上的指標後,我們來看看他們各自的意義:
- MSE = 0.08 表示預測的房價和實際房價之間的平均平方誤差為 0.08 百萬台幣。較低的 MSE 表明模型預測較為準確,但這個數字的絕對大小需要根據具體問題的尺度來解釋。
- RMSE = 0.283 表示模型預測的房價和實際房價之間的平均差異約為 0.283 百萬台幣。
- MAE = 0.24 表示模型預測的房價與實際房價之間的平均絕對差異為 0.24 百萬台幣。
- R² = 0.987 表示模型能解釋房價變異的 98.7%。這是一個很高的解釋能力,意味著模型非常有效地捕捉到了輸入特徵與房價之間的關係。
聚類問題的評估指標
聚類問題涉及無標籤數據的分組,常見的評估指標包括:
- 輪廓係數(Silhouette Score):這個指標衡量了樣本在自己的聚類內的緊密度與最近鄰近聚類的分離度。輪廓係數越高,表示聚類效果越好。例如在客戶分群中,如果輪廓係數高,表示客戶群體內部相似度高,且與其他群體有明顯區別。
- 使用時機:當我們需要評估聚類的質量,特別是在不知道真實標籤的情況下。
- 代表含義:衡量了樣本在自己的聚類內的緊密度與最近鄰近聚類的分離度。範圍從 -1 到 1,越接近 1 表示聚類效果越好。
- 注意事項:對於密度不均勻或形狀不規則的聚類可能不太適用。
- 戴維斯-鮑丁指數(Davies-Bouldin Index):這個指標衡量聚類的緊密度和分離度,值越小表示聚類效果越好。例如在基因表達數據分析中,如果戴維斯-鮑丁指數為 0.5,表示基因組之間有良好的分離。
- 使用時機:當我們需要評估聚類的緊密度和分離度,特別是在比較不同聚類算法時。
- 代表含義:衡量聚類的緊密度和分離度,值越小表示聚類效果越好。
- 注意事項:這個指標假設聚類是凸的(類似圓形或橢圓形),對於其他形狀的聚類可能不太準確。
- 相互資訊(Mutual Information):這是一種資訊理論的指標,用來衡量聚類結果與真實分類的相關性。在文檔分類中,如果相互資訊為 0.8,表示聚類算法產生的類別與預定義的文檔類別有很高的一致性。
- 使用時機:當我們有真實標籤並想衡量聚類結果與真實分類的相關性時。
- 代表含義:用來衡量聚類結果與真實分類的相關性。值越高表示聚類結果越接近真實分類。
- 注意事項:相互資訊不受標籤替換的影響,但可能難以直觀理解。
降維問題的評估指標
降維問題旨在減少數據的維度,常見的評估指標包括:
- 解釋變異量(Explained Variance):這個指標衡量了降維後數據保留的原始數據變異量的比例。較高的解釋變異量表示降維後的數據能較好地代表原始數據。例如在進行主成分分析(PCA)時,如果前兩個主成分的解釋變異量為 0.85,表示這兩個主成分捕捉了 85% 的原始數據變異。
- 使用時機:當我們需要評估降維後的數據保留了多少原始數據的資訊。
- 代表含義:衡量了降維後數據保留的原始數據變異量的比例。範圍從 0 到 1,較高的值表示降維後的數據能較好地代表原始數據。
- 注意事項:這個指標可能會忽視一些重要但變異較小的特徵。
- 重構誤差(Reconstruction Error):這個指標衡量了原始數據與通過降維後重建的數據之間的差異。重構誤差越小,表示降維效果越好。例如在圖像壓縮中,如果重構誤差為 0.05,表示壓縮後的圖像與原圖像只有 5% 的差異,保留了大部分視覺資訊。
- 使用時機:當我們需要評估降維後的數據能多好地重建原始數據時。
- 代表含義:衡量了原始數據與通過降維後重建的數據之間的差異。重構誤差越小,表示降維效果越好。
- 注意事項:重構誤差可能會受到異常值的影響,需要謹慎處理。
模型比較與選擇
通常在訓練模型時,我們會多方嘗試不同模型,不會只訓練單一模型,因此會需要進行不同演算法的比較。在完成模型訓練和評估後,通常會有多個模型可以選擇。模型比較的目的是從中選出最適合特定應用場景的模型。以下是幾種常見的模型比較與選擇方法:
1)基於評估指標的比較(Evaluation Metrics Comparison):
- 描述:將不同模型在同一數據集上的評估指標(如 MSE、R²、F1-score、Silhouette Score等)進行比較,選擇在關鍵指標上表現最佳的模型。
- 適用場景:適合有明確性能指標要求的情況,例如在回歸問題中,選擇具有最低 MSE 的模型。
2)模型複雜度的考量(Model Complexity Consideration):
- 描述:除了性能指標外,也需要考慮模型的複雜度(如參數數量、運算成本)。通常在多個性能相近的模型中,選擇較簡單的模型以降低過擬合風險並提高模型解釋性。
*適用場景:適合在預算有限或需要實時應用的場景中使用,選擇性能與複雜度之間平衡的模型。
3)泛化能力的比較(Generalization Ability Comparison):
- 描述:通過比較模型在驗證集或交叉驗證中的表現,選擇具有更強泛化能力的模型,即能夠在未見數據上保持較好性能的模型。
- 適用場景:適合在應用場景中數據變化多樣、希望模型能夠適應不同數據集的情況。
4)模型解釋性與可解釋性(Model Interpretability):
- 描述:有時候,模型的解釋性比單純的性能更重要。選擇那些更容易解釋的模型(如線性回歸、決策樹),特別是在需要向非技術人員解釋模型決策過程的應用中。
- 適用場景:適合在需要模型結果具備高可解釋性或受到法規要求的領域,例如金融或醫療。
5)外部驗證(External Validation):
- 描述:將模型應用於新的數據集或實際場景中進行測試,選擇在真實環境中表現最好的模型。
- 適用場景:適合需要確保模型能夠在不同環境中穩定運行的應用,例如部署到生產環境前的最後測試。
結論
在處理任何類型的問題時,選擇合適的評估指標很重要。透過比較不同模型的評估指標,考量模型的複雜度與泛化能力,以及其解釋性與可解釋性,最終可以選擇出最適合特定應用場景的模型,從而在實際應用中獲得最佳效果。而在選定了演算法後,往往希望可以做一些微調手法以進一步優化模型,這也將是下一章節的重點 -- 模型優化。

,其中 y_i 為真實數據, ŷ_i 為預測數據
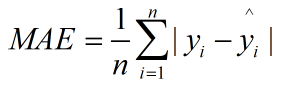 ,其中 y_i 為真實數據, ŷ_i 為預測數據
,其中 y_i 為真實數據, ŷ_i 為預測數據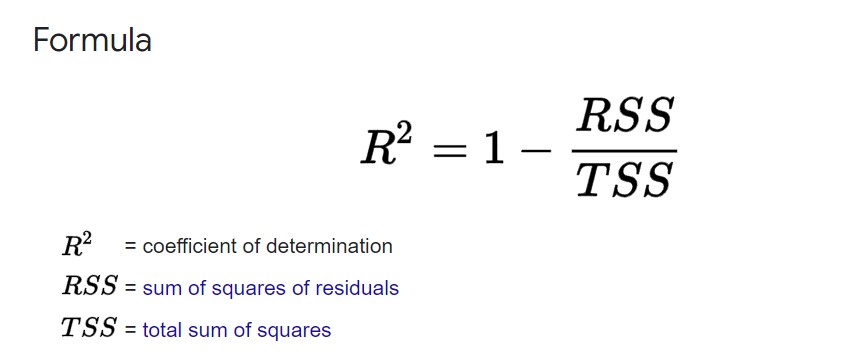
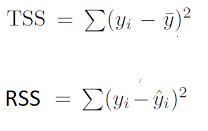 ,其中 y_i 為實際值,ŷ_i 為預測值,ȳ 為實際值的平均數
,其中 y_i 為實際值,ŷ_i 為預測值,ȳ 為實際值的平均數