前言：比賽倒數第二篇了＞＜這也是我最後一篇學習分享了，最後一天會講一些比賽心境或完賽結語之類的。那今天就來學習一下要如何建立變異數分析表吧。如果內容哪裡有錯誤的地方，請再多多包容了～

正文開始-->
變異數分析，是把全部觀察值的總變異分解成組間變異和誤差變異，然後將組間變異與隨機誤差進行比較，從而判斷總體均數間的差別是否具有統計學意義。

題目：使用變異數分析法，判斷三種甘藷品種的平均蛋白質含量是否有顯著差異。
欲檢定H0： μA= μB= μC v.s. H1： μA， μB， μC不全相等。

範例程式碼

rm(list=ls())
anova.tab <- function(fm) {
  tab <- summary(fm)
  k <- length(tab[[1]]) - 2
  temp <- c(sum(tab[[1]][, 1]), sum(tab[[1]][, 2]), rep(NA, k))
  tab[[1]]["Total", ] <- temp
  return(tab)
}
potato <- data.frame(X = c(7, 8, 5, 4, 9, 8, 6, 5, 10, 13, 11, 10), 
                     trt = gl(3, 4, labels = c("A", "B", "C")))
potato.anova <- aov(X ~ trt, data = potato)
anova.tab(potato.anova)

程式碼說明

• 清空環境：rm(list=ls())，清空R環境中所有物件。
• 定義 ANOVA 表的函數
  • anova.tab 函數接受一個線性模型（fm）作為參數。
  • 使用 summary(fm) 獲取 ANOVA 結果的摘要。
  • k 是自由度的數量，從 ANOVA 表中獲取。
  • 計算總和並將其放入 ANOVA 表的「Total」行中，然後返回完整的表格。
• 創建數據框：potato 數據框包含一個數值向量 X 和一個因子 trt，後者有三個水平（"A"、"B"、"C"），每個水平有 4 個觀測值。
• 顯示 ANOVA 表：anova.tab（potato.anova）

使用範例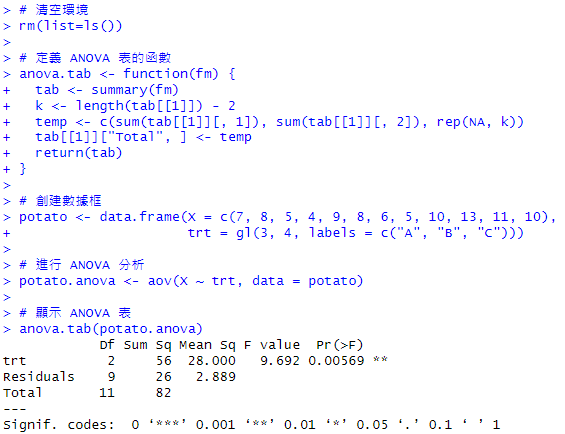

變數說明

• 來源（Source）：包括因素（trt）和誤差（Residuals），以及總和（Total）。
• 平方和（Sum Sq）：每個來源的平方和，用來衡量變異。
• 自由度（Df）：每個來源的自由度。
• 均方（Mean Sq）：平方和除以自由度，顯示每單位的變異。
• F 值（F value）：均方之比，用來檢驗因子是否顯著。
• P 值（Pr(>F)）：顯示因子是否對結果有顯著影響的統計值。

輸出結果說明：因p值=0.00569小於0.05，因此拒絕H0，代表μA， μB， μC不全相等。