註：本文同步更新在Notion!（數學公式會比較好閱讀）

前饋式神經網路是深度學習中最基本的網路結構，而梯度下降法則是訓練這類網路的重要手段。

梯度下降（Gradient Descent）是一種迭代優化算法，用於尋找某個損失函數的最小值。對於神經網路，損失函數描述了預測結果與實際目標之間的差異，最小化損失函數意味著我們的模型越來越準確。

梯度指向的是損失函數上升最快的方向，因此，梯度下降法通過以下公式更新參數，沿梯度的相反方向進行搜索，直到找到局部最小值：

前饋式神經網路中的梯度下降

在前饋式神經網路（FNN）中，神經元的權重和偏置需要通過梯度下降法來更新。為了了解梯度下降在 FNN 中如何應用，我們首先需要回顧神經網路的前饋過程和損失函數。

1. 前饋過程

2. 損失函數

3. 反向傳播與梯度計算

要更新權重W和偏置b，我們需要計算損失函數對這些參數的梯度。這過程通過**反向傳播算法（Backpropagation）**實現。

反向傳播計算的是損失函數對於每一層參數的偏導數，從而可以用於更新參數。

利用鏈式法則，這些梯度可以逐層從輸出層反向傳播到輸入層。

具體的梯度更新公式為：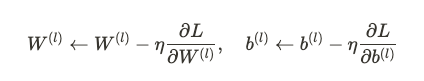

這一過程需要計算每一層輸出的梯度，再通過反向傳播更新權重和偏置。

梯度下降的變體

在實踐中，梯度下降法有多種變體，旨在提升收斂速度並解決大數據問題。常見的梯度下降變體包括：

1. 批量梯度下降（Batch Gradient Descent, BGD）

BGD 使用所有訓練樣本來計算梯度，因此每次更新都相對準確，但在大數據集下計算成本較高。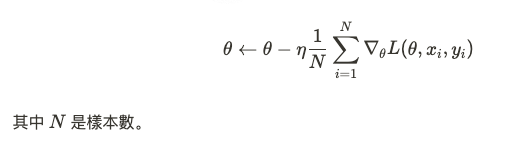

2. 隨機梯度下降（Stochastic Gradient Descent, SGD）

SGD 每次更新只使用一個樣本，雖然每次更新的方向較為隨機，但能夠加速收斂，尤其適用於大規模數據集。

3. 小批量梯度下降（Mini-Batch Gradient Descent）

小批量梯度下降結合了 BGD 和 SGD 的優點。每次更新使用一個小批量的數據，既保留了 BGD 的穩定性，又具有 SGD 的速度優勢。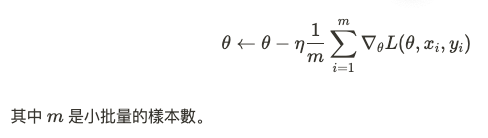

4. 動量法（Momentum）

動量法引入了過去梯度的影響，使得優化過程更具平滑性，能夠加快收斂速度並防止陷入局部最小值。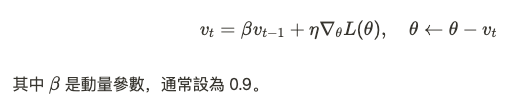

梯度下降的挑戰與解決方案

1. 學習率的選擇：
   學習率 η 太大會導致震盪，太小會使收斂過慢。常見的解決方案是使用學習率衰減，隨著訓練過程的進展逐漸降低學習率。
2. 梯度消失與爆炸問題：
   尤其在深度網路中，梯度消失或爆炸會使網路無法有效訓練。ReLU 等激活函數和權重初始化技巧（如 Xavier 或 He 初始化）可以緩解這些問題。
3. 局部最小值與鞍點：
   神經網路的損失函數可能存在局部最小值或鞍點，使梯度下降陷入困境。動量法、隨機梯度下降等技術能夠幫助逃離這些點。

通過反向傳播算法，我們可以計算損失函數對於每一層參數的梯度，並通過梯度下降更新權重和偏置，最終實現模型的優化。‹‹( ˙▿˙　)/››‹‹(　˙▿˙ )/››